从递归到记忆化搜索再到动态规划(原理+编程实例)

0. 概念

将原问题拆解成若干子问题，同时保存子问题的答案，使得每个子问题只求解一次，最终获得原问题的答案。
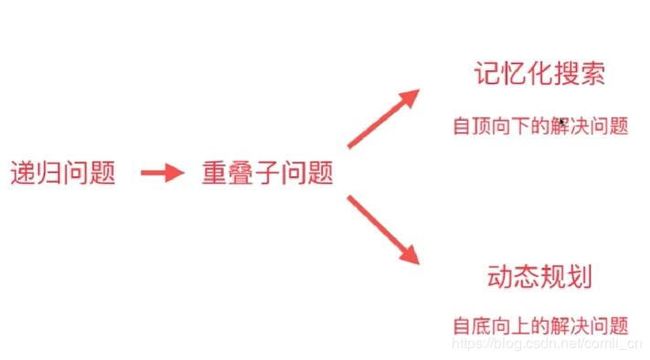
这个概念听起来跟带记忆的递归(即记忆化搜索)是一样的，其实本质上就是相同的，如果要分清楚的话可以参考下图。都是用于解决递归问题，且都能够避免重复计算重叠子问题，不同之处在于记忆化搜索是自顶向下解决问题的，而动态规划是自底向上解决问题的。但是有时候会将这两种形式都归为动态规划。

1. 算法设计步骤

(1)刻画一个最优解的结构特征
(2)递归地定义最优解的值
(3)计算最优解的值，通常采用自底向上的方法
(4) 利用计算出的信息构造一个最优解

2.斐波那契数列

在递归和带记忆的递归（原理和例子）这篇博文中我们讨论了计算斐波那契数列的普通递归方法和加了记忆的递归方法(即记忆化搜索)，这里接着讨论如何使用动态规划来计算斐波那契数列：

def fibonacci(n):
    memo = [-1]*(n+1)
    memo[0] = 0
    memo[1] = 1
    for i in range(2,n+1):
        memo[i] = memo[i-1]+memo[i-2]
    return memo[n]

print(fibonacci(6))

结果为：8

从计算斐波那契数列的例子中就可以感受到记忆化搜索是先假定$f(n-1)$已知，然后计算$f(n)$的时候再一层一层往下计算，而使用动态规划是先从$f(1)$和$f(2)$开始一点一点往$f(n)$求，这就是自顶向下和自底向上的区别。

3. 钢条切割

Serling公司购买长钢条，将其切割为短钢条出售。切割工序本身没有成本支出。公司管理层希望知道最佳的切割方案。假定我们知道Serling公司出售一段长为i英寸的钢条的价格为$p_i$(i=1,2,…，单位为美元)。钢条的长度均为整英寸。图15-1给出了一个价格表的样例。

钢条切割问题是这样的：给定一段长度为n英寸的钢条和一个价格表$p_i$(i=1,2,…n)，求切割钢条方案，使得销售收益$r_n$最大。注意，如果长度为n英寸的钢条的价格$p_n$足够大，最优解可能就是完全不需要切割。

(1)普通递归

分析：
如果我们切下来的第一段长度为$i$，则收益为$p_i$加上剩余长度钢条切割所得的收益，也就是说这个问题与它的子问题的形式是一样的，所以可以想到能使用递归的方法来解决。

def cut_rod(p, n):
	if n == 0:
		return 0
	q = -1
	for i in range(1, n+1):
		q = max(q, p[i]+cut_rod(p, n-i))
	return q

p = {1:1, 2:5, 3:8, 4:9, 5:10, 6:17, 7:17, 8:20, 9:24, 10:30}
for i in range(1, 11):
	n = i
	result = cut_rod(p, n)
	print(result)

结果为：

1
5
8
10
13
17
18
22
25
30

(2)记忆搜索

设定一个记忆单元，对每一个长度钢条的最高收益做一个记录，从而避免重复计算。

def cut_rod(p, n, memo):
	if n == 0:
		return 0
	if memo[n] >= 0:
		return memo[n]
	q = -1
	for i in range(1, n+1):
		q = max(q, p[i]+cut_rod(p, n-i, memo))

	memo[n] = q
	return q


p = {1: 1, 2: 5, 3: 8, 4: 9, 5: 10, 6: 17, 7: 17, 8: 20, 9: 24, 10: 30}

for i in range(1, 11):
	n = i
	memo = [-1]*(n+1)
	result = cut_rod(p, n, memo)
	print(result)

结果为：

1
5
8
10
13
17
18
22
25
30

(3) 动态规划

不管是普通递归还是记忆搜索都是自顶向下地解决问题，这里用自底向上的思路来解决一下。动态规划的思路是先将$n=0$是的最优收益表示出来并记住，然后基于这个再计算$n=1$时的最优收益，依次往下直到计算出$n$时的最优收益。

def cut_rod(p, n):
        r = [-1]*(n+1)
        r[0] = 0
        for i in range(1, n+1):
                q = -1
                for j in range(1, i+1):
                        q = max(q, p[j]+r[i-j])
                r[i] = q
        return r[n]


p = {1: 1, 2: 5, 3: 8, 4: 9, 5: 10, 6: 17, 7: 17, 8: 20, 9: 24, 10: 30}

for i in range(1, 11):
	n = i
	result = cut_rod(p, n)
	print(result)

结果为：

1
5
8
10
13
17
18
22
25
30