首先,容我吐槽一下这篇论文的行文结构、图文匹配程度、真把我搞得晕头转向,好些点全靠我猜测推理作者想干嘛,
背景
我们知道传统的CNN针对的是image,是欧氏空间square grid,那么使用同样square grid的卷积核就能对输入的图片进行特征的提取。在上一篇论文中,使用的理论是频域卷积(Spectral-domain),背后理论有点复杂。
这篇文章则从空域卷积(Spatial-domain)角度出发,直观上十分容易理解。
作者是这样想的:我们的image的一个个像素格子,可以看成规则的graph的结点,而在卷积的时候,当卷积核移动到如下位置(虚方框),我们可以将绿色点看成中心点,卷积则变成了将绿色中心点以及其一阶邻居同卷积核对应空间顺序的node,进行加权求和。进行类比,如下图右边,我们怎么设计一个合理的图卷积核呢?倘若设计合理,那么CNN的成熟理论便能借鉴过来使用

类比关键点
我们想要进行类比,首先的几个特点观察CNN:
中心点邻居个数
将image各个小格子像素看成graph中的node之后,这个graph是规整的,我们在围绕中心点(如上图绿点)卷积,当CNN中设计好stride和padding之后,CNN角度的卷积过程——>可以看作——>不断围绕中心点以及其一阶邻居进行加权求和。而且移动中心点之后,其一阶邻居个数均相同,这样带来的好处就是卷积核的node可以固定下来(即感受野范围可以固定)
但是,我们给的任意图,选好一些中心点之后,每个中心点的邻居个数各不相同。所以会出现当卷积核感受野范围确定了,但是只能在图中的一些中心点使用的问题,不能全局使用。
猜测:那是不是可以对邻居个数不够(或太多)的做padding增加(或cropping削减)操作呢?

中心点邻居顺序
在CNN进行卷积操作的时候,卷积核参数和image上感受野上的像素值是有一定空间对应关系的。好比\(3*3\)图片值,排列成1-9,同对应的卷积核1-9序号加权求和。
可是,我们的graph并没有结点的排列顺序,所以,在实现卷积之前,需要对中心结点+邻居结点,进行一定的排序
猜测:使用一个\(funtion\)将邻居进行排序?
其实上述还有个问题,就是中心点的选择,将CNN类比成graph之后,可以看见并不是每一个node都是中心点,所以图卷积也一样,需要先选定一些中心点(比如选前\(w\)个度较大的)
同时当我们将实现graph上的一层卷积之后,得到的数据就成了同CNN种一致的\(n\)维数据,至此以后,便能使用CNN中使用的手段继续往后操作

上图,就是图的一层卷积的大致实现步骤
- 第一层是在graph中选择\(w\)个中心点(红色)
- 第二层是选择每个中心点的\(k\)个邻居
- 第三层是将上述每一个中心点以及其邻居通过一个\(function\)进行排序,同卷积核对应位置进行加权求和实现一层卷积
论文内容
作者针对上面两个问题,提出将以下几个步骤解决来解决:
- Node Sequence Selection:将graph结点进行(简单理解按照度?)排序,选择前\(w\)个结点作为中心点
- Neighborhood Assembly:将上一步选择的\(w\)中心结点,分别找它们的一阶邻居(或者数量不够则二阶邻居)选择前\(k\)个当作该中心点的卷积操作时的邻居
- 有了以上两个步骤,就分别有了\(w\)个团(即\(w\)个中心结点)
- Graph Noermalization:将得到的\(w\)个团进行正则化,包括对邻居进行排序,邻居太多了则cropping,太少了则padding dummy node等
- Convolutional Architecture:然后将上述\(w\)个团,包含点和边的特征进行拼接,目的是拼接成规整的特征形式,方便后续的直接使用CNN的方法(可详见后面示意图)
Node Sequence Selection Alg.1
中心结点选择算法
其中\(labeling\) \(procedure\) \(l\)是用于对结点排序的一个\(function\),其设计目的:结构角色相同的两个结点,在各自图(graph)中应该得到相近的“标签”。\(w\)是中心结点个数(如果个数不够,则添加 \(dummy node\)),\(k\)是感受野,即邻居个数。这个function的设计其实是论文的核心,不过作者没给出具体形式(NP-Hard),给了两个定理,也没咋看明白,不细说

第6行是,选择中心结点邻居并正则化(涉及Alg.2和 Alg.3)

Neighborhood Assembly Alg.2
中心结点的邻居选择算法
是通过BFS完成的,\(k\)是邻居个数,一阶邻居不够则遍历二阶邻居...

Graph Noermalization Alg.3
主要对邻居结点个数的正则化,处理个数太多或太少情况,即第三行算法 Alg.4

Graph Noermalization Alg.4
邻居结点的正则化,进行padding 和 cropping 操作

Convolutional Architecture
上述几个过程的总体流程如下:
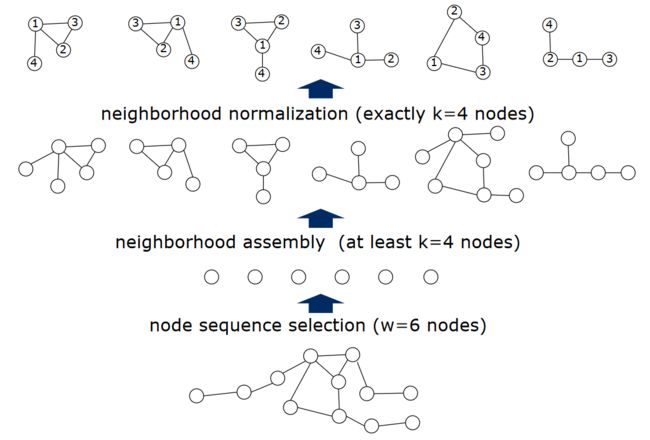
那么,我们现在基本就解决了文初的两个问题,感受野确定了,卷积核也可在全图上使用,那么就能同CNN一样,实现图上卷积了:
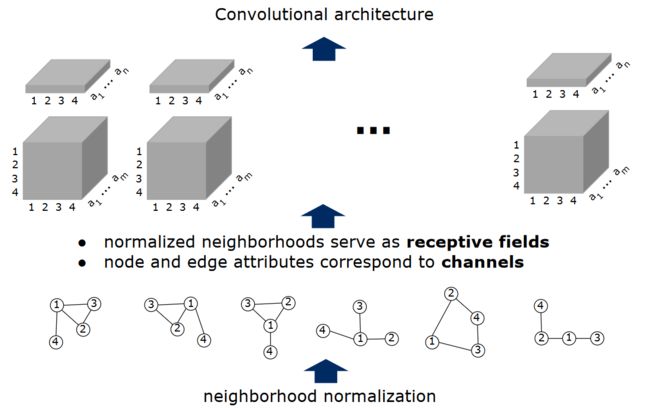
如上图所示,因为共\(w\)个中心点,即有\(w\)个感受野需要卷积,将上图每块感受野的node和edge分别使用向量表示(通过\(label function\)我们已经有了每个感受野中node的序号)。其中一层的扁平的是node信息(四个结点,每个结点特征\(a_{n}\)维),正方体是edge信息(边同样\(a_{n}\)维)
好,那么类比CNN,卷积进一步如下:

其中,粉红方块就是卷积核,绿色即通过一次卷积之后得到的。如果\(stride=4\),则每个灰色小方块恰为一个感受野:

经过这么一次的卷积,得到的数据已经同CNN无异了,正式从非欧数据转成了欧数据,后续可继续设计
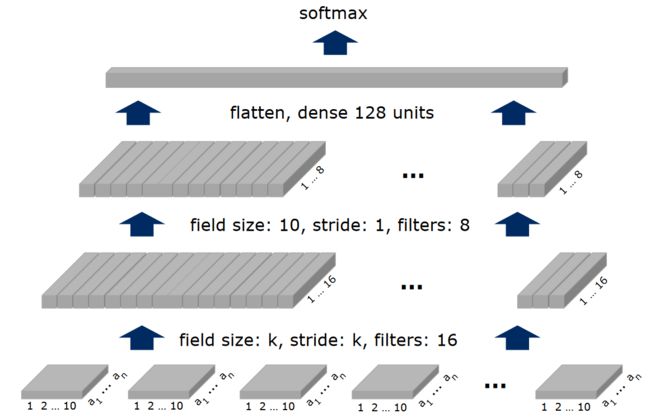
参考
https://link.zhihu.com/?target=https%3A//arxiv.org/pdf/1605.05273v2.pdf
https://link.zhihu.com/?target=https%3A//arxiv.org/pdf/1605.05273v2.pdf
https://zhuanlan.zhihu.com/p/27587371