四分位数是统计学里一个很重要的概念,实际应用中,所画出来的箱图,就使用到了这个概念,只有懂了四分位的概念才能看懂箱图所表达的意思。我这里通过一个实际的案例来说明四分位数的求取过程。
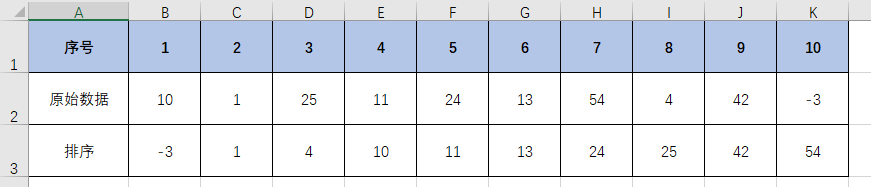
首先我们看下数据的情况,如下图所示,数据的总个数为10个
1、在求取四分位数据时,首先必须做的是要对数据进行升序排序,如下图。
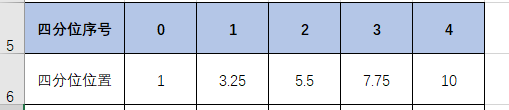
2、四分位求取,首先需要得出该四分位数的位置,如下是四分位数在排序后数据中的位置的公式
在Excel中使用以上的公式来计算第0、1、2、3、4个四分位值处的位置,得出如下结果
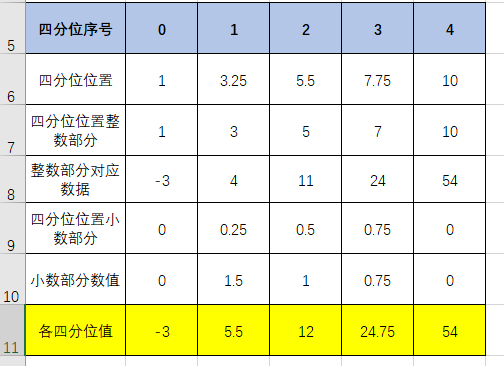
3、四分位数的求取,使用的是以下所说明的一套计算规则
公式可能看起来较为复杂,说明一下:
1、四分位数最终的结果由2部分相加得到,其一是四分位位置的整数部分对应的数据,其二是四分位位置的小数部分乘以差值得到
2、差值是四分位位置整数部分对应数据的下一个数据减去四分位位置整数部分对应的数据。
在Excel中将上面那个公式实现的结果如下:
注意:如果数据的总个数n减去1,得到的结果是4的整数倍的话,那么四分位数的位置都是整数值,各四分位数就可以在升序排序后的数列中直接找到,否则就需要通过以上方式计算小数部分。
例如:n的值为5、9、13等等,就是可以在数列中直接找到各四分位数。
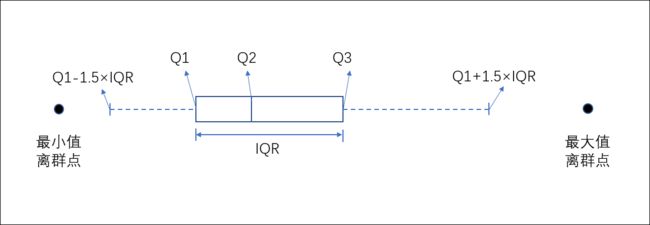
最后我们用一张图来看看箱图中各个图形元素:
1、Q1表示第1个四分位值,Q2表示第2个四分位值,即中位数,Q3表示第3个中位数
2、IQR是第3个中位数与第1个中位数的差值
3、虚线最左侧的划线表示Q1-1.5倍IQR,虚线最右侧的划线表示Q1+1.5倍IQR
4、左右的黑点是离群点,最左侧的离群点是最小值,最右侧离群点是最大值
从以上结果可以解答以往对四分位数的误区:
1、四分之一分位数并非中位数的2倍,也并非是四分之三分为的3倍
2、不要将箱图虚线左右侧的划线理解为四分之0分位,四分之四分位值,这2个分位值分别是最小值和最大值,它们可能会成为离群点