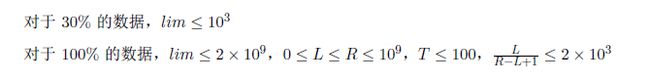Description
小Y 最近学习了线段树,但是由于她的智商比较低,运用的还不是很熟练。于是小R 给了她一点练习题训练,其中有一道是这样的。
这是小R 写的线段树的一段建树代码:
只要调用buildtree(1,0,n) 就可以得到一颗线段树了。显然,一颗线段树一共有O(n) 个节点,因为每一个节点都代表了一个不同的区间,所以线段树上一共出现了O(n) 个不同的区间。
现在小R 给了你一个区间[l; r],他想要你告诉他一个最小的n 使得区间[l; r] 出现在了用buildtree(1,0,n) 建出来的线段树中。
Input
第一行输入一个正整数T 表示数据组数。
接下来T 行每行三个整数L;R; lim 表示一组询问,如果对于所有的0 <= n <= lim 都不存在满足条件的解,输出-1 即可。
Output
对于每组询问输出一个答案。
Sample Input
2
0 5 10
6 7 10
Sample Output
5
7
.
.
.
.
.
分析
我们可以从该区间逆向推它的父节点
以该区间为左子树或为右子树
共有四种情况:
q=y-x+1;
dfs(x-q,y);
dfs(x-q-1,y);
dfs(x,y+q-1);
dfs(x,y+q);
一定注意剪枝,没做好可能会直接爆蛋
.
.
.
.
.
程序:
#include
#include
#include
using namespace std;
long long l,r,lim;
long long minn;
void dfs(long long x,long long y)
{
if (y>lim) return;
if (y>=minn) return;
if (x==0)
{
minn=y;
return;
}
long long q=y-x+1;
if (x-q==0||x-q>=q+q) dfs(x-q,y);
if (x-q==1||x-q-1>=q+q+1) dfs(x-q-1,y);
if (x>=q+q-1) dfs(x,y+q-1);
if (x>q+q) dfs(x,y+q);
}
int main()
{
int t;
scanf("%d",&t);
while (t--)
{
scanf("%lld%lld%lld",&l,&r,&lim);
if (r>lim)
{
printf("-1\n");
continue;
}
if (l>r)
{
printf("-1\n");
continue;
}
minn=2147483647;
dfs(l,r);
if (minn!=2147483647)
{
if (minn<=lim) printf("%lld\n",minn); else printf("-1\n");
} else printf("-1\n");
}
return 0;
}