深度学习论文笔记(可解释性)——CAM与Grad-CAM
文章目录
- 主要工作
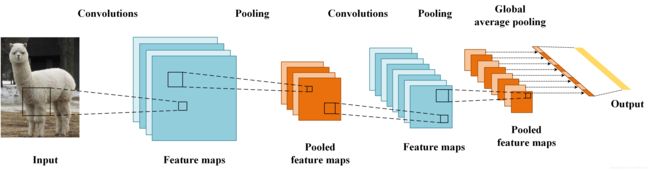
- Global Average Pooling的工作机制
- CAM
- Grad-CAM
主要工作
CAM与Grad-CAM用于解释CNN模型,这两个算法均可得出 c l a s s a c t i v a t i o n m a p p i n g class\ activation\ mapping class activation mapping(类似于热力图),可用于定位图像中与类别相关的区域(类似于目标检测),如下图所示:
五颜六色的区域即为类别相关的区域,表明了CNN为什么如此分类,比如CNN注意到了图中存在牙齿,因此将该图分为Brushing teeth。
阅读了三篇论文,总体来说收获有:
- 明白全局池化(Global Average Pooling)为什么有效
- 明白CAM与Grad-CAM可视化的原理
需注意,CAM与Grad-CAM的可视化只可以解释为什么CNN如此分类,但是不能解释CNN为什么可以定位到类别相关的区域
Global Average Pooling的工作机制
设类别数为 n n n,最后一层含有 n n n个特征图,求每张特征图所有像素的平均值,后接入一个有 n n n个神经元的全连接层,这里有两个疑问
为什么要有 n n n个特征图
论文的解释为“the feature maps can be easily interpreted as categories confidence maps.”。
这么做效果好是前提,对此的解释便是,每个特征图主要提取了某一类别相关的某些特征,例如第 i i i张特征图主要提取图中与飞机相关的部分,第 i + 1 i+1 i+1张特征图主要提取图中与汽车相关的部分。
论文在CIFAR10上训练完模型后,最后一层特征图可视化的结果如下:

从图来看,基本满足论文的解释
求完平均后接入全连接,这么做的理由亦或是好处是什么
下一节的“为什么如此计算可以得出类别相关区域”部分解释
CAM
CNN一般有特征提取器与分类器组成,特征提取器负责提取图像特征,分类器依据特征提取器提取的特征进行分类,目前常用的分类器为MLP,目前主流的做法是特征提取器后接一个GAP+类别数目大小的全连阶层。
CNN最后一层特征图富含有最为丰富类别语意信息(可以理解为高度抽象的类别特征),因此,CAM基于最后一层特征图进行可视化。
CAM将CNN的分类器替换为GAP+类别数目大小的全连接层(以下称为分类层)后重新训练模型,设最后一层有 n n n张特征图,记为 A 1 , A 2 , . . . A n A^1,A^2,...A^n A1,A2,...An,分类层中一个神经元有 n n n个权重,一个神经元对应一类,设第 i i i个神经元的权重为 w 1 i , w 2 i , . . . , w n i w_1^i,w_2^i,...,w_n^i w1i,w2i,...,wni,则第 c c c类的 c l a s s a c t i v a t i o n m a p p i n g class\ activation\ mapping class activation mapping(记为 L C A M c L_{CAM}^c LCAMc)的生成方式为:
L C A M c = ∑ i = 1 n w i c A i (式1.0) L_{CAM}^c=\sum_{i=1}^{n}w_i^cA^i\tag{式1.0} LCAMc=i=1∑nwicAi(式1.0)
图示如下:
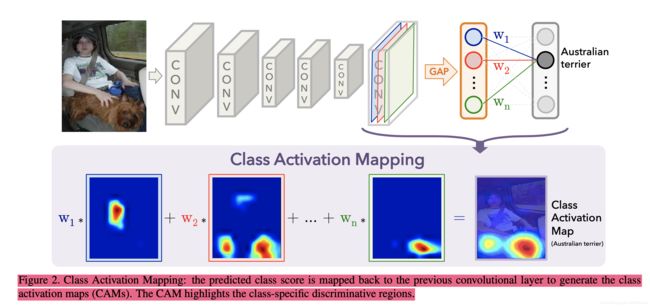
生成的Class Activation Mapping大小与最后一层特征图的大小一致,接着进行上采样即可得到与原图大小一致的Class Activation Mapping
为什么如此计算可以得出类别相关区域
用GAP表示全局平均池化函数,沿用上述符号,第 c c c类的分类得分为 S c S_c Sc,GAP的权重为 w i c w_{i}^c wic,特征图大小为 c 1 ∗ c 2 c_1*c_2 c1∗c2, Z = c 1 ∗ c 2 Z=c_1*c_2 Z=c1∗c2,第 i i i个特征图第 k k k行第 j j j列的像素值为 A k j i A^i_{kj} Akji,则有
S c = ∑ i = 1 n w i c G A P ( A i ) = ∑ i = 1 n w i c 1 Z ∑ k = 1 c 1 ∑ j = 1 c 2 A k j i = 1 Z ∑ i = 1 n ∑ k = 1 c 1 ∑ j = 1 c 2 w i c A k j i \begin{aligned} S_c&=\sum_{i=1}^{n}w_i^cGAP(A_i)\\ &=\sum_{i=1}^nw_i^c\frac{1}{Z}\sum_{k=1}^{c_1}\sum_{j=1}^{c_2}A_{kj}^i\\ &=\frac{1}{Z}\sum_{i=1}^n\sum_{k=1}^{c_1}\sum_{j=1}^{c_2}w_i^cA_{kj}^i \end{aligned} Sc=i=1∑nwicGAP(Ai)=i=1∑nwicZ1k=1∑c1j=1∑c2Akji=Z1i=1∑nk=1∑c1j=1∑c2wicAkji
特征图中的一个像素对应原图中的一个区域,而像素值表示该区域提取到的特征,由上式可知 S c S_c Sc的大小由特征图中像素值与权重决定,特征图中像素值与权重的乘积大于0,有利于将样本分到该类,即CNN认为原图中的该区域具有类别相关特征。式1.0就是计算特征图中的每个像素值是否具有类别相关特征,如果有,我们可以通过上采样,康康这个这个像素对应的是原图中的哪一部分
GAP的出发点也是如此,即在训练过程中让网络学会判断原图中哪个区域具有类别相关特征,由于GAP去除了多余的全连接层,并且没有引入参数,因此GAP可以降低过拟合的风险
可视化的结果也表明,CNN正确分类的确是因为注意到了原图中正确的类别相关特征
Grad-CAM
CAM的缺点很明显,为了得出GAP中的权重,需要替换最后的分类器后重新训练模型,Grad-CAM克服了上述缺点。
设第 c c c类的分类得分为 S c S_c Sc,GAP的权重为 w i c w_{i}^c wic,特征图大小为 c 1 ∗ c 2 c_1*c_2 c1∗c2, Z = c 1 ∗ c 2 Z=c_1*c_2 Z=c1∗c2,第 i i i个特征图第 k k k行第 j j j列的像素值为 A k j i A^i_{kj} Akji。
计算 α i c = 1 Z ∑ k = 1 c 1 ∑ j = 1 c 2 ∂ S c ∂ A k j i \alpha_i^c=\frac{1}{Z}\sum_{k=1}^{c_1}\sum_{j=1}^{c_2}\frac{\partial S_c}{\partial A^i_{kj}} αic=Z1k=1∑c1j=1∑c2∂Akji∂Sc
Grad-CAM的Class Activation Mapping计算方式如下:
L G r a d − C A M c = R e L U ( ∑ i α i c A i ) L_{Grad-CAM}^c=ReLU(\sum_{i}\alpha_i^cA^i) LGrad−CAMc=ReLU(i∑αicAi)
之所以使用ReLU激活函数,是因为我们只关注对于类别有关的区域,即特征图取值大于0的部分
Grad-CAM为什么这么做呢?具体的推导位于快点我,我等不及了,推导比较简单,这里就不敲了,直接贴图
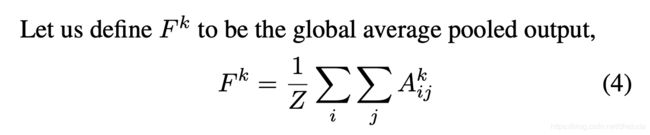

最后三个式子漏了符号 ∂ \partial ∂,总的来说还是非常惊喜的,如果CAM在可视化的过程中,将特征图进行了归一化,则有
L C A M c = 1 Z ∑ i = 1 n w i c A i = 1 Z ∑ i = 1 n ∑ k = 1 c 1 ∑ j = 1 c 2 ∂ S c ∂ A k j i A i L_{CAM}^c=\frac{1}{Z}\sum_{i=1}^{n}w_i^cA^i=\frac{1}{Z}\sum_{i=1}^n\sum_{k=1}^{c_1}\sum_{j=1}^{c_2}\frac{\partial S_c}{\partial A^i_{kj}}A^i LCAMc=Z1i=1∑nwicAi=Z1i=1∑nk=1∑c1j=1∑c2∂Akji∂ScAi
Grad-CAM是CAM的一般化。