算法和数据结构笔记(一) 基本数据结构

---

1 动态数组

它的基本思路是使用如malloc/free等内存分配函数得到一个指向一大块内存的指针，以数组的方式引用这块内存或者直接调用动态数组的接口，根据其内部的实现机制自行扩充空间，动态增长并能快速地清空数组，对数据进行排序和遍历。(在理解C语言(一)中介绍了动态数组，这里不再赘述)

它的数据结构定义如下:

typedef struct {
    void *data; 
    int capacity;
    int index;
    int type_size;
    int (*comp)(const void *,const void *);
} array_t;

• data表示: 指向一块连续内存的指针;type_size: 元素类型的大小(动态执行时才能确定类型)
• capacity: 动态数组的容量大小，最大可用空间 ; index: 动态数组的实际大小
• int (*comp)(const void *,const void *): 元素的大小比较函数,comp为函数指针

它的实现参考: 动态数组接口实现

---

2 链表

链式存储是最通用的存储方式之一，它不要求逻辑上的相邻的元素物理位置上相邻，仅通过链接关系建立起来。链表解决了顺序表需要大量的连续存储空间的缺点，但链表附加指针域，也带来了浪费存储空间的缺点。

它有多种多样的结构，如:

• 只含一个指针域的单链表、
• 含指向前后结点两个指针域的双链表
• 首尾相连的循环链表（单向或双向）
• 块状链表(chunklist)
• 跳跃链表

---

A 单链表
对于链表这种结构，有时候第一个节点可能会被删除或者在之前添加一个节点，使得头指针指向的节点有所改变。消除这些特殊情况的方法是在链表的第一个节点前存储一个永远不会被删除的虚拟节点,我们称之为头节点，头结点的数据域可以不设任何信息也可以记录表长等信息。

头结点的指针域指向的是真正的第一个节点，从实现中可以看到它极大地简化了插入和删除操作，也避免了在C中使用二级指针跟踪记录头指针的变化。参考理解C语言(一)关于二级指针使用的解释。为了比较使用头结点和不使用头结点的区别，实现的单链表采取不使用头结点的方法，双向循环链表使用头结点，加深对链表操作的理解。

B 块状链表
对于块状链表来说，它本身是一个链表，但链表存储的每个结点是一个数组。如果数组有序，结合链表的顺序遍历(链表是非随机访问的)和有序数组的折半查找可以加快数据的查找速度，在某些情况下对于特殊的插入或删除，它的时间复杂度O(n^(1/2))
并且相对于普通链表来说节省内存，因为它不用保存指向每一个数据结点的指针。

C 跳表
对于跳跃链表，它是一种随机化的数据结构，在有序的链表上增加附加的前进链接，增加是以随机化的方式进行的，所以列表的查找可以快速跳过部分列表而得名。在实际中它的工作性能很好 ，这种随机化平衡方案比在平衡二叉树中用到的确定性平衡方案更容易实现，并且在并行计算中也很有用。引用跳表的发明者William Pugh的话

跳跃列表在很多应用中有可能替代平衡树而作为实现方法的一种数据结构。它的算法有着同平衡树以线性对数的渐进预期时间边界，并且更简单、更快速和使用更少的空间。

2.1 单链表

链表中节点类型描述如下:

typedef struct list_node {
    void *item;
    struct list_node *next;
} list_node_t;

对应地，单链表的数据结构定义如下:

typedef struct slist {
    list_node_t *head;
    int n;
    int (*comp)(const void *,const void *);
} slist_t;

这里的head指针既可以定义为头指针，指向链表的第一个节点，即空表初始化为NULL；它也可以定义为虚拟的头结点，分配一个节点的内存，它的指针域指向链表的实际结点。这里先使用不带头结点的方法实现单链表的操作

2.1.1 单链表的插入和删除操作

A 单链表的删除操作
如果在链表尾部插入，要考虑如果链表为空的话尾部的插入同样需要更新头指针，它的实现如下:

/*在单链表尾部添加元素*/
void slist_push_back(slist_t *l,void *item) {
    /*构造新结点*/
    list_node_t *node=new_list_node(item);

    if(l->head){
        list_node_t *cur=l->head;
        while(cur->next){
            cur=cur->next;
        }
        cur->next=node;
    } else {
        l->head=node;
    }
    l->n++; 
}

在链表头部添加元素比较简单，实现如下:

/*在单链表头部添加元素*/
void slist_push_front(slist_t *l,void *item) {
    list_node_t *node=new_list_node(item);
    node->next=l->head;
    l->head=node; //无需区分头指针是否为空，情形一样
    l->n++;
}

因而如果插入的节点是链表的第i个位置，就需要讨论插入的情形: 头部插入、尾部插入、中间插入，这里不给出具体实现。

B 单链表的删除操作
如果在链表尾部删除元素，分两种情形删除: 链表只有一个节点时、链表不止一个结点。对于含有多个结点的链表，需要维持一个prev指针记录尾部元素的上一个结点再进行删除操作。实现如下:

/*在单链表尾部删除元素,若存在，返回被删除的元素键值，否则返回NULL*/
void *slist_pop_back(slist_t *l) {
    list_node_t *cur,*prev;
    if(l->head){
        void *res_item;
        if(l->head->next){ //不止一个结点
            prev=l->head;
            cur=l->head->next;
            while(cur->next){ 
                prev=cur;
                cur=cur->next;
            }
            prev->next=NULL;
        } else { //只有一个节点
            cur=l->head;
            l->head=NULL;
        }
        res_item=cur->item;
        free(cur);
        l->n--;

        return res_item;
    } 
    return NULL;
}

在链表头部删除元素比较简单，实现如下:

/*在单链表头部删除元素，若存在返回被删除的元素键值，否则返回NULL*/
void *slist_pop_front(slist_t *l) {
    list_node_t *cur;
    if(l->head){
        cur=l->head;
        l->head=l->head->next;

        void *res_item=cur->item;
        free(cur);
        l->n--;
        return res_item;
    } 
    return NULL;
}

另外一个删除操作是：删除单链表中第一个含item值的节点，它的实现和尾部删除类似，同样需要讨论删除情形。具体实现如下:

/*在单链表中找到第一个含item值的节点并删除此节点*/
void *slist_delete(slist_t *l,void *item) {
    list_node_t *cur,*prev;
    int (*comp)(const void *,const void *);
    comp=l->comp;
    prev=NULL;
    cur=l->head;
    while(cur){
        int cmp_res=comp(item,cur->item);
        if(cmp_res==0){
            break;
        } else {
            prev=cur;
            cur=cur->next;
        }
    }
    if(cur==NULL){ //该键值不存在或者链表为空
            return NULL;
    } else {
        if(prev==NULL) //删除的是第一个节点
            return slist_pop_front(l);
        else {
            prev->next=cur->next;
            void *res_item=cur->item;
            free(cur);
            l->n--;
            return res_item;
        }
    }
}

2.2 双向循环链表

双向循环链表中的节点类型描述如下:

typedef struct dlist_node {
    void *item;
    struct dlist_node *prev;
    struct dlist_node *next;
} dlist_node_t;

对应地，双向循环链表的数据结构定义如下:

typedef struct {
    dlist_node_t *head;
    int n;
    int (*comp)(const void *,const void *);
} dlist_t;

/*创建一个元素节点，让头尾都指向自己并设元素值*/
static inline dlist_node_t *new_dlist_node(void *item){
    dlist_node_t *node=malloc(sizeof(dlist_node_t));
    node->prev=node->next=node;
    node->item=item;
    return node;
}

在双向循环链表的实现中，使用的head指针为虚拟的头结点，实现方式如下:

/**
 * 为双向循环链表分配内存,两种思路:
 * 不带头节点，通过判断l->head是否为NULL来删除链表
 * 带头节点，只需判断cur=l->head->next与l->head的是否相等(l->head==l->head->next才为链表空)
 * 单链表实现中使用了不带头节点的办法(注释说明的头结点只是链表头指针)，双向链表我使用带头节点的思路
 * 也是为了比较这两种方法哪个适合简化插入和删除操作
 */
dlist_t *dlist_alloc(int (*comp)(const void *,const void *)){
    dlist_t *l=malloc(sizeof(dlist_t));
    l->head=new_dlist_node(NULL); 
    l->n=0;
    l->comp=comp;
    return l;
}

从后面的实现可以看出它极大简化了链表的插入和删除操作。

2.2.1 循环双链表的插入和删除操作

由于使用的是带头结点的循环双链表，它判空的标志是l->head==l->head->next，一定要明确，这是判断遍历是否结束的标记。

A 查找循环双链表中第i个位置的结点
为了简化插入和删除操作，假设第0个位置的节点为虚拟的头结点(很关键)，使得插入和删除完全统一起来实现如下:

/*查找双链表第pos个位置的节点，pos从0开始*/
dlist_node_t *dlist_find_pos(dlist_t *l,int pos){
    if(pos<0 ||pos>l->n){
        printf("Invalid position to find!\n");
        return NULL; 
    } 

    if(pos==0){
        return l->head; //头部插入，关键点，使得所有插入统一化了
    }

    dlist_node_t *cur=l->head->next;
    int j=1;//计数从1开始表示
    while(cur!=l->head){ //链表为空的标志
        if(j==pos){
            break;
        }
        cur=cur->next;
        j++;
    }
    return cur;
}

B 插入操作
在双向循环链表某位置添加元素，可插入的pos范围: 0-l->n

• pos为0时表示头部插入
• pos为l->n时表示尾部插入

关于双链表的插入方式，tmp指针要插入在cur指针后,要么两节点前驱后后继同时链上，要么先链一个方向再链另外一个方向，方式不同效果相同。实现的技巧就在于基于位置查找的函数在pos=0时返回头指针，使得插入任何位置都使用统一的代码。 实现如下:

void dlist_insert(dlist_t *l,void *item,int pos){
    if(pos<0|| pos>l->n){
        printf("Invalid position");
        return;
    }
    dlist_node_t *cur=dlist_find_pos(l,pos);//定位到pos位置的节点
    dlist_node_t *tmp=new_dlist_node(item); ;//插入到pos位置的新节点
    tmp->next=cur->next;
    cur->next->prev=tmp;
    tmp->prev=cur;
    cur->next=tmp;
    l->n++;
}

C 删除操作
删除操作的思路是要先找到删除位置的前驱结点，当删除的是第一个结点时由于位置查找的函数同样也可以返回第0个位置的结点指针(返回头结点)，同样使得删除操作都可以使用一致的代码。实现如下:

/*在双向循环链表中删除pos位置节点并输出当前值，pos从1到l->n*/
void *dlist_delete(dlist_t *l,int pos){
    if(pos<1|| pos>l->n){
        printf("Invalid position");
        return NULL;
    }
    dlist_node_t *cur=dlist_find_pos(l,pos-1);//找到删除位置的前驱节点
    dlist_node_t *tmp=cur->next; //被删除位置的节点

    cur->next=tmp->next;
    tmp->next->prev=cur;
    void *res_item=tmp->item;
    free(tmp);
    l->n--;
    return res_item;
}

2.2.2 链表的实现

• 单链表
• 双向链表

2.3 跳跃表skiplist

在字典的实现中，通常使用平衡二叉树会得到较好的性能保证，例如AVL tree、Red-Black tree、Self-adjusting trees。对于除伸展树外(单个操作是O(n)的时间复杂度)的一些平衡树,它们的插入、删除等操作一般有对数级别的时间复杂度。但它们的缺点是需要维护二叉树平衡的信息，在实现上有一定的难度，显然数据结构的随机化比维护平衡信息更容易实现。

参考William Pugh论文的描述，定义跳跃表节点和跳跃表的数据结构如下:

typedef struct skiplist_node {
    void *item;
    struct skiplist_node *forward[1];
} skiplist_node_t;

typedef struct {
    skiplist_node_t *head;
    skiplist_node_t **update;
    double prob;
    int max_level;
    int level;
    int (*comp)(const void *,const void *);
    int n;
} skiplist_t;

为了灵活性，在跳表结点的结构定义中，把结点指向某个含有键值对的表项而非整数键

• item: 表示结点的数据项
• forward: 长度为1的柔性数组，切记节点的大小包括一个数组元素(与长度为0的数组大小不想同)
• 柔性数组: 表明每个节点对应的forward数组是变长的

在跳表的数据结构定义中:

• head: 为了简化插入和删除操作，定义一个虚拟头结点，它含有最大层次+1个forward前向指针
• update数组: 用于在插入、删除、查找操作中更新每个层级被查找节点的前驱指针。它在跳表初始化时就被创建，防止了每次在进行插入等操作时需要分配和释放该数组的内存
• prob: 某节点被创建时出现在某层次的概率。 它的概率分布类似于丢硬币实验，连续i次出现同种情形(如正面)对应i的次数的分布。很显然它满足参数为p的几何分布，期望值为1/p
• level: 跳表当前的最大层次
• comp: 比较跳表中表项大小的函数
• n: 当前存储在跳表中的元素个数

根据William Pugh的分析，建议我们理想中开始查找的层次为L(N)=log(N)/log(1/p)。例如p=0.5时，处理至多含有2^16个数据的跳表最大的层次是16，即定义中的max_level。

2.3.1 跳表的插入、删除、查找操作

A 跳表的初始化和节点层次的随机化生成
在初始化跳表时需要明确几点:

• 跳表的最大层次的计算公式: int max_level= -log(N)/log(prob);。例如prob=0.5,8个节点的跳表它应该有0,1,2,3层
• 链表头结点有max_level+1个前向指针，从0开始初始化(头结点本身含有1个level 0级别的前向指针，再加上借助柔性数组扩展的max_level个前向指针)
• 对于某层次i的前向指针为NULL表示该层级上的虚拟链表为空
• 为防止每次插入或删除操作时要重复分配update数组预先初始化

它实现如下:

skiplist_t *skiplist_alloc(int capacity,double prob,int (*comp)(const void *,const void *)){
    skiplist_t *l=malloc(sizeof(skiplist_t));
    l->prob=prob;
    l->comp=comp;
    /*注gcc的数学函数定义在libm.so文件例，需链接上数学库，编译时添加 -lm选项*/
    int max_level= -log(capacity)/log(prob);//这个指的是最高的层级max_level,例如8个节点的话有0,1,2,3层
    l->max_level=max_level; //例如max_level为16
    l->level=0;
    l->head=new_skiplist_node(max_level,NULL);
     
    /*更新头结点的forward数组为NULL*/
    for(int i=0;i<=max_level;i++){
        l->head->forward[i]=NULL;
    }

    /*为防止每次插入或删除操作时要重复分配update数组*/
    l->update=malloc((max_level+1)*sizeof(skiplist_node_t *));
    l->n=0;
    return l;
}

节点层次的随机化生成，要点有两个:

• 链表的层次为i,表示若随机生成的level大于i则i层次以上的前向指针均指向为NULL
• 生成的level值范围是0-max_level,但这种随机数的生成效果并不是最佳的，它也可能出现某些层次以上的元素完全相同

它的实现如下:

int rand_level(double prob,int max_level){
    int level;
    int rand_mark=prob*RAND_MAX;
    for(level=0; rand()

B 跳表的插入和删除操作
插入和删除操作的核心在于简单的搜索和拆分(要么插入要么删除)。通过查找键在每个层次所属的位置，记录在一个update数组中。update[i]表示的是插入和删除位置的最右左边位置(个人称之为插入或删除位置的前驱指针)。如下图:

插入操作的要点如下:

• 找到待插入的位置(在当前元素的前向指针的键与元素的键相等或者大于的适合退出)，再更新每个层次的update数组
• 随机生成新节点的level
• 调整指向，插入新节点

删除操作的要点如下:

• 找到要调整位置的前驱指针
• 自底层向高层进行节点的删除并释放该节点内存
• 更新跳表的level（由于某些节点的删除可能会使部分高层次的前向指针为NULL）

查找操作就比较简单，它是插入或删除操作的第一个步骤。三个操作的实现如下:

void *skiplist_insert(skiplist_t *l,void *item){
    skiplist_node_t *cur=l->head;
    skiplist_node_t **update=l->update;
    int (*comp)(const void *,const void *);
    comp=l->comp;
    int i;
    /*查找键所属的位置*/
    for(i=l->level;i>=0;i--){
        while(cur->forward[i]!=NULL &&comp(cur->forward[i]->item,item)<0)
            cur=cur->forward[i]; //在当前层次遍历直至前向指针为NULL或者对应的前向指针的元素大于或等于item
        update[i]=cur; //更新插入位置的前驱指针
    }
    cur=cur->forward[0];
    if(cur!=NULL&&comp(cur->item,item)==0)
        return cur->item; //键值已存在，直接返回原来的节点

    int level=rand_level(l->prob,l->max_level); //最大的level控制在max_level
    if(level> l->level){ //如果新生成的层数比跳表层数大，更新下标大于i的update数组指向为头结点
        for(i=l->level+1;i<=level;i++){ //持续到当前生成的level上
            update[i]=l->head;
        }
        l->level=level; //更新自己的层级数
    }
    skiplist_node_t *tmp=new_skiplist_node(level,item);

    /**
     * 调整前向指针的指向，插入新结点
     * 问题就出现在这里，注意如果生成的level级别较低，只需要在从0..level的级别进行插入，切记不能使用l->level
     * l->level和level是有不同的，除非level大于当前跳表的level时
     */
    for(i=0;i<=level;i++){ 
        tmp->forward[i]=update[i]->forward[i];
        update[i]->forward[i]=tmp;
    }
    l->n++;
    return NULL;
}

/*在跳表中进行查找，找到返回当前元素的item否则返回NULL*/
void *skiplist_find(skiplist_t *l,void *key_item){
    /*查找是否含有当前的元素*/
    skiplist_node_t *cur=l->head;
    skiplist_node_t **update=l->update;
    int (*comp)(const void *,const void *);
    comp=l->comp;
    int i,res;
    for(i=l->level;i>=0;i--){
        while(cur->forward[i]!=NULL &&((res=comp(cur->forward[i]->item,key_item))<0))
            cur=cur->forward[i]; //在当前层次遍历直至前向指针为NULL或者对应的前向指针的元素大于或等于item
        update[i]=cur; //更新插入位置的前驱指针
    }
    cur=cur->forward[0];
    if(cur!=NULL&&comp(cur->item,key_item)==0){
        return cur->item;
    }
    return NULL;
}


void *skiplist_delete(skiplist_t *l,void *item){
    skiplist_node_t *cur=l->head;
    skiplist_node_t **update=l->update;
    int (*comp)(const void *,const void *);
    comp=l->comp;
    int i;
    int level=l->level;
    for(i=level;i>=0;i--){
        while(cur->forward[i]&&comp(cur->forward[i]->item,item)<0)
            cur=cur->forward[i];
        update[i]=cur;
    }
    cur=cur->forward[0];
    if(cur==NULL||comp(cur->item,item)!=0) return NULL; //键值不存在


    for(i=0;i<=level;i++){
        if(update[i]->forward[i]!=cur) break; //若低层次的前向指针不包括cur，则高层次就不可能存在(高层次的链表是低层次的子链表)
        update[i]->forward[i]=cur->forward[i];
    }
    void *ret_item=cur->item;
    l->n--;
    free(cur);

    while(l->level>0 &&l->head->forward[l->level]==NULL)
        l->level--;
    return ret_item;
}

它的完整实现如下: 跳跃表的实现

2.3.2 总结

尽管跳表在wort-case时会生成一个糟糕的不平衡结构，没法和平衡树一样保证较好的最坏或均摊的性能，但发生这个情形的概率很小。并且它在实际工作中效果很好，对于很多应用来说，随机化的平衡方法-跳跃链表相比平衡树树而言，它是一种更自然的表示，并且算法更为简单，实现起来更为容易，比平衡树具有更好的常数优化性能。

下面是一些使用跳表的应用和框架列表，可见相比平衡树，跳跃表还是有很多实际应用的

• Lucene: 使用跳表在对数时间内search delta-encoded posting lists
• Redis: 基于跳表实现它的有序集合
• nessDB: a very fast key-value embedded Database Storage Engine (Using log-structured-merge (LSM) trees), uses skip lists for its memtable
• skipdb: 一个开源的基于跳跃表实现的可移植的支持ACID事务操作的Berkeley DB分割的数据库
• ConcurrentSkipListSet and ConcurrentSkipListMap in the Java 1.6 API.
• leveldb: a fast key-value storage library written at Google that provides an ordered mapping from string keys to string values
• Skip lists are used for efficient statistical computations of running medians (also known as moving medians)。

另外跳跃表也可应用在分布式应用中，用来实现高扩展性的并发优先级队列和并发词典(使用少量的锁或者基于无锁)，所以学习基于随机化技术的跳跃表是很有必要的。

---

3 栈、队列

3.0 前言

栈是一种LIFO的数据结构，它只有一个出口，只允许在表的一端进行操作，如插入、删除、取得栈顶元素，不允许有其他方法可以存取栈的其他元素(没有遍历行为)。

队列是一种FIFO的数据结构，它有两个出口，限定只能在表的一端进行插入(队尾插入)和在另一端进行删除(队头删除)操作，同样的它也没有遍历行为。

3.1 栈

在栈的顺序存储结构中，一般设置一个top变量指向栈顶元素的下一个位置，初始化为0。如下为其重要操作：

• 栈为空的条件： top==0
• 压栈操作: stack[top++]=x
• 出栈操作： x=stack[--top]

如下为基于动态数组的栈定义。实现参考: 基于动态数组的栈实现

/*基于动态数组的栈结构定义*/
typedef struct {
    void *data;
    int capacity; //允许容纳最大容量
    int top; //当前栈顶的下一个位置
    int type_size; //元素类型的字节大小
} stack_t;

栈在括号匹配、表达式计算(中缀表示转后缀表示、后缀表达式计算)、进制转换、迷宫求解都有应用，它一般也作为递归算法的非递归表示。

3.2 队列

由于在队列的顺序存储中无法判断队列满的条件，一般地如果用数组实现队列，循环队列是必须的。一般设置一个队头指针front和队尾指针rear,初始化两变量均为0。为区分队空和队满，一般牺牲一个单元来区分队空和队满，这是种较为普遍的做法，约定以front在rear的下一个位置为队满标志(front指向队头元素的上一个元素，rear指向队尾元素)。如下为其重要操作:

• 队空标志: front==rear ； 队满标志： (rear+1)%MAXSIZE==front
• 入队操作: rear=(rear+1)%MAXSIZE; queue[rear]=x
• 出队操作: front=(front+1)%MAXSIZE; x=queue[front];

如下为基于动态数组的队列定义。实现参考: 基于动态数组的队列实现

注意以上两个是基于泛型的实现，在进行栈或队列操作时使用内存复制memcpy的行为，并非原始的数据地址，如果把其应用在二叉树的遍历算法中是存在bug的。

/**
 * 循环队列结构定义
 * 如果是固定长度的循环数组，一般建议牺牲一个单元来区分队空和队满
 * 入队时少一个单元，因而一般设定front指向队头的上一个元素，
 * rear指向队尾元素
 */
typedef struct {
    void *data;
    int capacity;
    int front; //指向队头元素的上一个元素
    int rear; //指向队尾元素
    int type_size;
} queue_t;

队列应用在在层次遍历、计算机系统的资源请求中，它的特点就是在进行当前层的处理时就对下一层数据进行预处理。

---

4 散列表Hashtable

散列表，又称哈希表，它是根据关键字而进行快速存取的技术，是一种典型的“空间换取时间”的做法。它是普通数组概念的推广，因为可以对数组进行直接寻址，故可以在O(1)时间内访问数组的任意元素。

它的思路是试图将关键字通过某种规则映射到数组的某个位置，以加快查找的速度。这种规则称之为散列函数，存放的数组称为散列表。散列表建立起了关键字和存储地址的一种直接映射关系，特别适合于关键字总数很多而存储在字典中的关键字集合很少的情形，尽管在最坏情况下，查找一个元素的时间为O(n),但在实际应用中，散列表的效率还是很高的，在一些合理的假设下，散列表查找的期望时间为O(1)。

使用散列的查找算法分为两步。第一步是用散列函数将查找的关键字转化为数组的一个索引。理想情况下，不同关键字都能映射为不同的索引值，当然，实际情况是我们需要面对多个不同的关键通过哈希函数得到相同的数组下标。我们称之为碰撞冲突。一方面，设计好的Hash函数应尽量减少这样的冲突，另一方面由于这样的冲突总是不可避免，所以我们要设计好处理碰撞冲突的方法。这是第二步。

4.1 散列函数和处理冲突的方法

构造散列函数要注意以下几点：

• Hash函数定义域必须包含全部关键字，而值域依赖于散列表的大小或地址范围
• 理想中的Hash函数计算出来的地址应该能等概率、均匀地分布在整个地址空间，以减少冲突的发生
• Hash函数应该尽量简单，能够在较短时间内计算出任意关键字的存储地址
• 所有散列函数都具有一个特性：如果两个散列值不想同，则两个散列值的原始输入也不相同

A 常用的散列函数

1. 直接定址法,计算简单，适合关键字分布基本连续的情况,H(key)= a*key+b
2. 除留余数法，最简单最常用，关键是选好质数p,保证散列的关键字等概率地映射到任一地址,p是一个不大于散列表长m,但最接近或等于m的质数H(key)= key %p
3. 数字分析法，若关键字是r进制数，在某些位可能分布均匀，应选择数码分布均匀的若干位作为散列地址适合于一个已知的关键字集合
4. 平方取中法

B 字符串Hash函数比较
还记得Java的字符串对象中hashCode的计算方法为什么经常用31来计算么？其实它是通过实验优化最终确定的。它是属于BKDRHash函数的一种，初始化种子为31。

例如一个日期类型，它对应的hashCode实现如下:

public class Date implements Comparable {
    private static final int[] DAYS={0,31,29,31,30,31,30,31,31,30,31,30,31};
    /*成员变量均为final类型，表示一经初始化就不可变化*/
    private final int month;
    private final int day;
    private final int year;

    public int hashCode() {
        int hash=17;
        hash=31*hash+month;
        hash=31*hash+day;
        hash=31*hash+year;
        return hash;    
    }

常见的字符串Hash函数有BKDRHash、APHash、DJBHash、JsHash、RSHash、SDBHash、PJWHash、ELFHash。各种字符串的哈希函数的评测参考Byvoid的这篇文章。它的结果显示BKDRHash无论是在实际效果还是编码实现中，效果都是最突出的，可以看到BKDRHash的种子选取是很有规律的31 131 1313 13131 etc..,非常适合记忆。

如下附有32位无符号的Hash函数的C代码:

// BKDR Hash Function
unsigned int BKDRHash(char *str)
{
    unsigned int seed = 131; // 31 131 1313 13131 131313 etc..
    unsigned int hash = 0;

    while (*str)
    {
        hash = hash * seed + (*str++);
    }

    return (hash & 0x7FFFFFFF);
}

unsigned int SDBMHash(char *str)
{
    unsigned int hash = 0;

    while (*str)
    {
        // equivalent to: hash = 65599*hash + (*str++);
        hash = (*str++) + (hash << 6) + (hash << 16) - hash;
    }

    return (hash & 0x7FFFFFFF);
}

// RS Hash Function
unsigned int RSHash(char *str)
{
    unsigned int b = 378551;
    unsigned int a = 63689;
    unsigned int hash = 0;

    while (*str)
    {
        hash = hash * a + (*str++);
        a *= b;
    }

    return (hash & 0x7FFFFFFF);
}

// JS Hash Function
unsigned int JSHash(char *str)
{
    unsigned int hash = 1315423911;

    while (*str)
    {
        hash ^= ((hash << 5) + (*str++) + (hash >> 2));
    }

    return (hash & 0x7FFFFFFF);
}

// P. J. Weinberger Hash Function
unsigned int PJWHash(char *str)
{
    unsigned int BitsInUnignedInt = (unsigned int)(sizeof(unsigned int) * 8);
    unsigned int ThreeQuarters    = (unsigned int)((BitsInUnignedInt  * 3) / 4);
    unsigned int OneEighth        = (unsigned int)(BitsInUnignedInt / 8);
    unsigned int HighBits         = (unsigned int)(0xFFFFFFFF) << (BitsInUnignedInt - OneEighth);
    unsigned int hash             = 0;
    unsigned int test             = 0;

    while (*str)
    {
        hash = (hash << OneEighth) + (*str++);
        if ((test = hash & HighBits) != 0)
        {
            hash = ((hash ^ (test >> ThreeQuarters)) & (~HighBits));
        }
    }

    return (hash & 0x7FFFFFFF);
}

// ELF Hash Function
unsigned int ELFHash(char *str)
{
    unsigned int hash = 0;
    unsigned int x    = 0;

    while (*str)
    {
        hash = (hash << 4) + (*str++);
        if ((x = hash & 0xF0000000L) != 0)
        {
            hash ^= (x >> 24);
            hash &= ~x;
        }
    }

    return (hash & 0x7FFFFFFF);
}

// DJB Hash Function
unsigned int DJBHash(char *str)
{
    unsigned int hash = 5381;

    while (*str)
    {
        hash += (hash << 5) + (*str++);
    }

    return (hash & 0x7FFFFFFF);
}

// AP Hash Function
unsigned int APHash(char *str)
{
    unsigned int hash = 0;
    int i;

    for (i=0; *str; i++)
    {
        if ((i & 1) == 0)
        {
            hash ^= ((hash << 7) ^ (*str++) ^ (hash >> 3));
        }
        else
        {
            hash ^= (~((hash << 11) ^ (*str++) ^ (hash >> 5)));
        }
    }

    return (hash & 0x7FFFFFFF);
}

C 工业界比较知名的Hash算法
这些算法通常应用于信息安全领域(MD: message digest缩写)

• MD4: 一种用来测试信息完整性的密码散列函数的实现。一般128位长度的MD4散列函数被表示为32字长的数字，并用高速软件实现
• MD5: 一种符合工业标准的单向128位哈希方案。以结果唯一并且不能返回其原始格式的方法来转换数据(如密码)。速度相比MD4更慢，但更安全，在抗分析和抗查分表现更好
• SHA-1: 由美国国安局设计，从一个最大的2^64位元的信息中产生一串160元的摘要。

一般地这些哈希算法在符号表或字典实现中代价很大，应用并不多，它们在信息安全领域主要应用在文件校验、数字签名、数字指纹和存储密码中(MD4,MD5,SHA-1已被确定不安全，SHA-2,WHIRLPOOL)

D 处理冲突的方法
在前言中谈到了任何散列函数都不可避免地遇到冲突，此时必须考虑冲突发生时应该如何进行处理，即为产生的关键字寻找下一个空的Hash地址，于是有各种处理冲突的方法

• 拉链法

这种方法是在每个表格元素中维护一个list,把所有冲突的关键字存储在同一个list中。使用开链法，表格的负载系数(表中记录数n/散列表长度m)大于1，它适用于经常进行插入和删除的情况。STL里面的hash table便采用了这种做法

• 开放定址法

这种方法是指可存放新表项的空闲地址，既向它的同义词表项开放，又向它的非同义词表项开放。递推公式为
\[ H_i=(H(key)+d_i)%m \]
其中i=1,2,...,k-1,m为散列表表长，增量序列d它通常有以下几种取法:

1) 线性探测法,特点是冲突发生时顺序查看表中的下一个单元，直至找到一个空单元或查遍全表，缺点是容易产生聚集现象
\[d_i=1,2,...,m-1\]

2) 二次探测法，表长m必须是4k+3的质数，可以很好的避免出现堆积问题，但无法探测到所有的单元
\[d_i=1,-1,4,-4,,...,k^2,-k^2,k <= m/2\]
3) 序列为伪随机数序列时，称为伪随机探测法
4) 当发生冲突时，利用另外一个哈希函数再次计算一个地址，直到不再发生冲突，称为再散列法

总结它有以下几个要点

• 在开放定址法中，不能随便地物理删除表中已有元素，因为若删除元素将会阶段其他具有相同散列地址的元素的查找地址。建议是采用惰性删除，即只标记删除记号，实际删除操作则待表格重新整理时再进行(rehashing)。可看出它的负载系数永远小于1，经理论分析，当负载因素为0.5时，查找命中所需要的探测次数为3/2，未命中的需要约5/2,所以保持散列表的使用率小于1/2即可获得一个较好的查找性能。
• ASL(成功): 搜索到表中已有元素的平均探测次数，平均的概念是针对表中当前非空元素，并非整个表长;ASL(不成功): 表中可能散列到的位置上要插入新元素时为找到空桶的探测次数的平均值，平均的概念是针对散列函数映射到的位置总数(有时候存在表长与散列表质数的选取不一致的情形)，一般是针对表长
• 拉链法更容易实现删除操作，如果散列函数设计得不好相比线性探测法对于聚集现象更不敏感；线性探测法更为节省内存空间，并且具有更好的Cache性能
• 散列表的查找效率取决于三个因素： 散列函数、处理冲突的方法和负载系数。

4.2 散列表实现

如下为基于拉链法的散列表节点和散列表数据结构的定义:

/*散列表结点元素的定义*/
typedef struct hash_tbl_node {
    void *item;
    struct hash_tbl_node *next;
} hash_tbl_node_t;


typedef struct {
    int num_buckets;
    int num_elements;
    hash_tbl_node_t **buckets;
    int (*hash_fcn)(const void *,int);
    int (*comp_fcn)(const void *,const void *);
} hash_tbl_t;

参数说明如下:

• num_elements: 散列表中元素(结点)的个数(用于动态调整表格大小，重建表格而用)
• buckets_num: 散列表的表格大小(表中的每个元素项称为桶),在STL中以质数来设计表格大小
• STL中甚至提供一个函数，用于查询在这28个作为表格大小的质数中，最接近某数并大于某数的质数
• buckets: 由指向链表的结点指针构成的数组
• hash_fcn: 针对元素表项键值的散列函数指针
• comp_fcn: 比较元素表项大小的函数指针

它的测试代码如下:

#define NUM_ITEMS 30
#define NUM_BUCKETS 17
#define RND_MAX 1000

typedef struct {
    int key;
    int val;
} test_item_t;

int comp_fcn(const void *a,const void *b){
    return ((test_item_t *)a)->key-((test_item_t*)b)->key;
}

int hash_fcn(const void *item, int n){
    /*将键值作为随机的种子*/
    // srand(((test_item_t *)item)->key);
    // rand();
    // return rand()%n;
    int key=((test_item_t *)item)->key;
    return  key% n;
}

void visit(hash_tbl_node_t *cur){
    if(cur){
        test_item_t *item=(test_item_t *)cur->item;
        printf("(%d , %d) ",item->key,item->val);
    }
}


void test(){
    test_item_t arr[NUM_ITEMS],*cur,*item;
    int i;
    for(i=0;ikey,cur->val);
            i--;
        } else{
            printf("Inserted key-val pair: (%d , %d)\n",item->key,item->val);
        }
    }
    

    printf("\n========散列表的重复插入测试========\n");
    test_item_t test_dup;
    test_dup.key=2*2;
    if(hashtbl_insert(tbl,&test_dup)){
        printf("Duplicate detected\n");
    } else {
        printf("No Duplicate\n");
    }

    printf("\n========散列表的查找测试========\n");
    test_item_t find_dup;
    for(i=0;i

4.2.1 散列表的插入、删除和查找操作

基于链表的操作由于比较简单，直接贴上代码网址,完整的散列表实现

如下为Java版的散列表实现:

• 基于拉链法
• 基于线性探测法

---

5 二叉树

5.0 前言

一般地二叉树多用链式存储结构来描述元素的逻辑关系。通常情况下二叉树中的结点定义如下:

typedef struct btree_node {
    void *item;
    struct btree_node *left;
    struct btree_node *right;
} btree_node_t;

在一些不同的实际应用中，还可以增加某些指针域或者线索化标志，例如增加指向父结点的指针、左右线索化的标志。

另外如果你想区分二叉树结点和二叉树这种结构，不妨定义如下的二叉树结构(类似于STL中分离定义数据结构和元素结点的方法):

typedef struct  {
    btree_node_t *root;
    int n;
    int (*comp)(const void *,const void *);
} btree_t;

typedef void (*cb)(btree_node_t *);//定义访问结点的函数指针

其中n表示二叉树结点的个数，comp表示函数指针。使用函数指针comp因为数据类型使用的是通用指针，在进行查找等比较数据大小的操作时需要定义一个比较函数，在泛型数据结构的C实现中应用非常广泛。

5.1 二叉树的遍历

二叉树常见的遍历次序有先序、中序、后序三种，其中序表示根结点在何时被访问。每种遍历算法都有对应的递归解法和非递归解法。它的非递归解法中使用了栈这种数据结构。每个遍历都有自身的特点：

• 先序遍历序列的第一个结点和后序遍历的最后一个结点一定是根结点
• 在中序遍历序列中，根结点将序列分成两个子序列: 根结点左子树的中序序列和根结点右子树的中序序列
• 先序序列或者后序序列或者层次序序列结合中序序列可以唯一确定一棵二叉树

二叉树还有一种层次序遍历，它是按自顶向下、自左向右的访问顺序来访问每个结点，它的实现使用了队列这种数据结构。

此外二叉树还有一种Morris遍历方法，和上面使用O(n)空间复杂度的方法不同，它只需要O(1)的空间复杂度。这个算法跟线索化二叉树很像，不过Morris遍历是一边建立线索一边访问数据，访问完后直接销毁线索，保持二叉树的不变。Morris算法的原则比较简单：借助所有叶结点的右指针(空指针)指向其后继节点，组成一个环，但由于第二次遍历到这个结点时，由于左子树已经遍历完了，就访问该结点。

总结下来，遍历是二叉树各种操作的基础，可以在遍历的过程中对结点进行各种操作，例如求二叉树的深度(高度)、二叉树的叶子结点个数、求某层结点个数(或者树的最大宽度、分层输出结点)、判断二叉树是否相同或者是否为完全二叉树或者二叉排序树、求二叉树中结点的最大距离、由遍历序列重建二叉树等。

5.1.1 遍历的递归解法

递归代码比较简单，就不具体解释了，实现如下:

/*先序遍历，递归*/
 void bt_preorder(btree_t *t, cb visit){
    bt_preorder_rec(t->root,visit);
 }

void bt_preorder_rec(btree_node_t *cur, cb visit) {
    if(cur==NULL) return ;
    visit(cur);
    bt_preorder_rec(cur->left,visit);
    bt_preorder_rec(cur->right,visit);
}

/*中序遍历，递归*/
void bt_inorder(btree_t *t, cb visit) {
    bt_inorder_rec(t->root,visit);
}

void bt_inorder_rec(btree_node_t *cur, cb visit) {
    if(cur==NULL) return ;
    bt_inorder_rec(cur->left,visit);
    visit(cur); 
    bt_inorder_rec(cur->right,visit);
}

/*后序遍历，递归*/
void bt_postorder(btree_t *t, cb visit) {
    bt_postorder_rec(t->root,visit);
}
void bt_postorder_rec(btree_node_t *cur, cb visit) {
    if(cur==NULL) return ;
    bt_postorder_rec(cur->left,visit);
    bt_postorder_rec(cur->right,visit);
    visit(cur);
}

5.1.2 基于栈或队列的非递归解法

A 基于栈的VLR先序遍历
整体思路：先入栈根结点，然后再判断栈是否为空：不为空，出栈当前元素，并按照右左子树顺序分别入栈。该方法可借助栈的操作，如下的方法采用了类似于栈的实现方式,注意入栈顺序: VRL。

实现如下:

void bt_preorder_iter(btree_t *t, cb visit){
    if(t->root){
        btree_node_t **stack=malloc(sizeof(btree_node_t *)*(t->n));
        stack[0]=t->root;
        int top=1;
        while(top>0){ //只要栈不为空
            btree_node_t *cur=stack[--top];//出栈
            visit(cur);
            if(cur->right)
                stack[top++]=cur->right;
            if(cur->left)
                stack[top++]=cur->left;

        }
        free(stack);
    }
}

B 基于栈的LVR中序遍历
整体思路：判断条件有两个：栈是否为空或当前结点cur是否为空。根据中序遍历顺序LVR

• 如果栈为空，需不断压栈当前每个非空结点一直遍历到第一个没有左孩子的根结点
• 此时cur为空，top(栈中的元素大小)只要大于0，开始进行出栈，访问当前结点,再遍历右子树

实现如下:

void bt_inorder_iter(btree_t *t, cb visit){
    btree_node_t **stack=malloc(sizeof(btree_node_t *)*(t->n));
    btree_node_t *cur=t->root;
    int top=0;
    while(top>0|| cur!=NULL){
        if(cur !=NULL){
            stack[top++]=cur;
            cur=cur->left;
        } else{
            cur=stack[--top];//出栈当前栈顶元素
            visit(cur);
            cur=cur->right;
        }
    }
    free(stack);
}

C 基于栈的LRV后序遍历
整体思路: 用栈存储结点时，必须分清返回根结点时：是从左子树返回的还是从右子树的返回的。这里用一个pre指针记录最近刚访问过的结点。当一直往左直到左孩子为空时,判断当前结点的右孩子是否为空或者是否已访问过

• 若右孩子为空或者已被访问过(LV或者LRV),则访问当前结点，并更新最近访问的结点，并重置当前指针为NULL
• 否则遍历右孩子(压栈)，再转向左

实现如下:

void bt_postorder_iter(btree_t *t, cb visit){
    btree_node_t **stack=malloc(sizeof(btree_node_t *)*(t->n));
    btree_node_t *cur=t->root;
    btree_node_t *pre=NULL; //指向最近访问过的结点
    int top=0;
    while(cur!=NULL||top>0){ //当前结点不为空或者栈不为空
        if(cur){ //压栈，一直往左走
            stack[top++]=cur; 
            cur=cur->left;
        } else {
            cur=stack[top-1];//取栈顶元素
            if(cur->right&&cur->right!=pre){ //如果右子树存在，且未被访问过
                cur=cur->right;
                stack[top++]=cur; //转向右，压栈
                cur=cur->left;//再走向最左，始终保持LRV的遍历顺序
            } else{ //要么右孩子为空，要么右孩子已经被访问过，弹出当前结点
                cur=stack[--top];
                visit(cur);
                pre=cur; //记录最近访问过的结点，结点访问完重置cur指针
                cur=NULL;
            }
        }
    }
    free(stack);
}

D 基于队列的层次序遍历
和先序遍历很类似，区别就是栈换成了队列。实现如下:

void bt_levelorder(btree_t *t,cb visit){
    if(t->root){
        int maxsize=t->n+1;//使用循环队列浪费1个空间
        btree_node_t **queue=malloc(sizeof(btree_node_t *)*maxsize);
        btree_node_t *cur;
        int front=0;
        int rear=0;
        rear=(rear+1)%maxsize;
        queue[rear]=t->root;
        while(front!=rear){ //判断队列是否为空
            front=(front+1)%maxsize;
            cur=queue[front];//出队
            visit(cur);
            if(cur->left){
                rear=(rear+1)%maxsize;
                queue[rear]=cur->left;  //入队
            }
            if(cur->right){
                rear=(rear+1)%maxsize;
                queue[rear]=cur->right;//入队
            }
        }
        free(queue);
    }
}

5.1.3 Morris遍历

A Morris中序遍历
步骤如下: 初始化当前节点cur为root节点

1. 若当前cur没有左孩子，直接访问当前结点，cur转向右孩子
2. 若cur有左孩子，先寻找到cur的前驱节点

• 如果前驱节点右孩子为空，记录前驱节点右孩子为当前结点，cur转向左孩子
• 如果前驱节点右孩子为当前节点，表明左孩子已被访问，将前驱节点右孩子重设为空;直接访问当前结点，cur转向右孩子

B Morris先序遍历
步骤如下: 初始化当前节点cur为root节点

1. 若当前cur没有左孩子，直接访问当前结点，cur转向右孩子
2. 若cur有左孩子，先寻找到cur的前驱节点

• 如果前驱节点右孩子为空，记录前驱节点右孩子为当前结点，访问当前节点，并将当前结点设置为已访问过的节点，cur转向左孩子
• 如果前驱节点右孩子为当前节点，表明左孩子已被访问，将前驱节点右孩子重设为空，cur转向右孩子

C Morris后序遍历
Morris后续遍历稍微麻烦点：它必须保证在访问某个当前节点时，左右子树的所有左孩子必须先被访问;而右孩子的输出从底部往顶部逆向访问就行

步骤如下：设置一个虚拟根结点，记它的左孩子为root,即当前cur为该虚拟根结点

1. 如果cur的左孩子为空，先记录会被访问的当前节点再转向右孩子分支
2. 如果cur的左孩子不为空，找到cur的前驱

• 如果前驱的右孩子为空，建立线索化，记录会被访问的当前节点再转向左孩子分支
• 如果前驱的右孩子为当前节点，表示已经线索化，因而逆向输出当前节点左孩子到该前驱节点路径上的所有节点,转向当前节点右孩子分支

实现如下:

void bt_morris_inorder(btree_t *t, cb visit){
    if(t->root){
        btree_node_t *cur=t->root;
        btree_node_t *pre; //前驱线索
        while(cur){
            if(cur->left==NULL){
                visit(cur);
                pre=cur; //记录已被访问的前驱
                cur=cur->right;
            } else{
                /*先找到cur的前驱节点*/
                btree_node_t *tmp=cur->left;
                while(tmp->right&&tmp->right!=cur)
                    tmp=tmp->right;

                if(tmp->right==NULL){ //表明左子树未访问，先建立线索再访问左子树
                    tmp->right=cur; 
                    cur=cur->left;//没有访问，无需记录pre指针
                } else { //左子树已被访问，则访问当前节点，恢复二叉树,遍历右子树
                    visit(cur);
                    tmp->right=NULL;
                    pre=cur;
                    cur=cur->right;
                }
            }
        }
    }
}

void bt_morris_preorder(btree_t *t, cb visit){
    if(t->root){
        btree_node_t *cur=t->root;
        btree_node_t *pre; //前驱线索
        while(cur){
            if(cur->left==NULL){
                visit(cur);
                pre=cur;
                cur=cur->right; //记录直接前驱，转向右孩子
            } else{
                btree_node_t *tmp=cur->left;
                while(tmp->right&&tmp->right!=cur)
                    tmp=tmp->right;

                if(tmp->right==NULL){ //表明右子树未被访问，访问当前节点，更新线索，转向左孩子
                    visit(cur); //仅这一行位置与中序不同
                    tmp->right=cur;
                    pre=cur;//标记当前节点被访问过(这个与visit函数在同一个代码段内)
                    cur=cur->left;
                } else { //表明左子树已被访问，重置线索，转向右孩子
                    tmp->right=NULL;
                    /*pre=cur; 不能有这句，因为cur早早被访问*/
                    cur=cur->right;
                }
            }
        }
    }
}

void bt_morris_postorder(btree_t *t, cb visit){
    if(t->root){
        btree_node_t *rec=malloc(sizeof(btree_node_t));
        rec->left=t->root; //创建一个dummy结点，它的左孩子指向根结点
        btree_node_t *cur=rec;//从虚拟根结点开始遍历
        btree_node_t *pre;
        while(cur){
            if(cur->left==NULL){
                pre=cur;//和前两个morris遍历不同，这种方法是先线索化后保证一侧子树都被访问完后直接逆向输出
                cur=cur->right;//一般是先访问后再记录被访问的节点，这次相反先记录将被访问的节点后再访问
            } else {
                btree_node_t *tmp=cur->left;
                while(tmp->right&&tmp->right!=cur)
                    tmp=tmp->right;

                if(tmp->right==NULL){ //还未线索化，未被访问，先建立线索
                    tmp->right=cur;//保证下一次循环时回到后继节点，此时已被线索化
                    pre=cur;//必须要有，先记录
                    cur=cur->left;
                } else{ //已建立线索
                    reverse_branch(cur->left,tmp,visit);
                    pre->right=NULL;
                    pre=cur; //必须要有
                    cur=cur->right;
                }

            }
        }
        free(rec);
    }
}

---

6 位示图: bit-map

6.0 位示图重要操作

一个unsigned int数能表示32个整数,整数从0开始,针对整数i:

• i对应的无符号数组下标索引slot: i/32
• i对应的索引内容里面的比特位数: i%32(1<<(i&0x1F)

因而在位数组中，必须提供三个重要操作:

• 清除位图某位: bm->bits[i/32] &= ~(1<<(i%32))
• 设置位图某位: bm->bits[i/32] |= (1<<(i%32))
• 测试位图某位: bm->bits[i/32] & (1<<(i%32))

这里采用位掩码运算的方法完成这些操作，避免取模和除数运算，效率更高

6.1 位示图的数据结构定义

位示图的数据结构定义如下:

/*位示图数据结构定义*/
typedef struct bitmap{
    unsigned int *bits;
    int size; //整数个数大小
} bitmap_t;

位示图函数的功能测试如下:

#include "bitmap.h"
#include 
#include 

#define MAX 10000
#define RAD_NUM 100

int main(){
    /*接受大小为MAX的参数，创建一个位图*/
    bitmap_t *bm=bitmap_alloc(MAX);

    unsigned int i;
    unsigned int arr[RAD_NUM];
    for(i=0;i< RAD_NUM;i++){
        arr[i]=RAD_NUM-i;
    }
    
    /**
     * 设置某些数在位图的位表示为1
     * 生成RAD_NUM个不相同的随机数据
     * 插入位图中，对应位则设置为1
     */
    printf("原始无序的数据:\n");
    for(i=0;i< RAD_NUM;i++){
        unsigned int j=i+rand()%(RAD_NUM-i);
        int temp=arr[i];
        arr[i]=arr[j];
        arr[j]=temp;
        printf("%d ",arr[i]);
        if(i%10==0&&i!=0) printf("\n");
        bitmap_set(bm,arr[i]);
    }
    printf("\n");
    
    printf("使用位图排序后的数据:\n");

    /*查询该数是否在数组中，很容易保证有序输出*/
    for(i=0;i< MAX;i++){
        if(bitmap_query(bm,i)){
            printf("%d ",i);
            if(i%10==0&&i!=0) printf("\n");
        }
    }
    printf("\n");

    /*释放位图的内存*/
    bitmap_free(bm);
    return 0;
}

6.2 位示图的核心实现

核心的实现还是清除、设置和测试某个位，代码如下:

/*分配指定size大小的位示图内存*/
bitmap_t *bitmap_alloc(int size){
    bitmap_t *bm=malloc(sizeof(bitmap_t));
    bm->bits=malloc(sizeof(bm->bits[0])*(size+BITS_LENGTH-1)/BITS_LENGTH); //计算合适的slot个数
    bm->size=size;
    memset(bm->bits,0,sizeof(bm->bits[0])*(size+BITS_LENGTH-1)/BITS_LENGTH);
    return bm;
}

/*释放位图内存*/
void bitmap_free(bitmap_t *bm){
    free(bm->bits);
    free(bm);
}

/**
 * 一个unsigned int数能表示32个整数,整数从0开始,针对整数i:
 * i对应的无符号数组下标索引slot: i/32
 * i对应的索引内容里面的比特位数: i%32(1<<(i&MASK)
 * 
 * 清除位图某位: bm->bits[i/32] &= ~(1<<(i%32))
 * 设置位图某位: bm->bits[i/32] |= (1<<(i%32))
 * 测试位图某位: bm->bits[i/32] & (1<<(i%32))
 * 这里采用位掩码运算的方法完成这些操作，避免取模和除数运算，效率更高
 */

/**/
void bitmap_clear(bitmap_t *bm,unsigned i){
    if(i>=bm->size){
        printf("Invalid integer\n");
        return ;
    }
    bm->bits[i>>SHIFT] &= ~(1<<(i & MASK));
}

/*设置位图中的某一位*/
void bitmap_set(bitmap_t *bm,unsigned i){
    if(i>=bm->size){
        printf("Invalid integer\n");
        return ;
    }
    bm->bits[i>>SHIFT] |= (1<<(i & MASK));
}

/*查询位图中的某一位,该位为1，返回true;否则返回false*/
bool bitmap_query(bitmap_t *bm,unsigned i){
    if(i>= bm->size)
        return false;
    if( (bm->bits[i>>SHIFT]) & (1<<(i & MASK)))
        return true;
    return false;
}

位示图的完整实现

6.3 Bloom Filter

---

7 并查集: union-find

7.0 前言

在某些应用中，要将n个不同的元素分成一组不相交的集合。在这个集合上，有两个重要的操作: 找出给定的元素所属的集合和合并两个集合。再例如处理动态连通性问题，假定从输入中读取了一系列整数对，如果已知的数据可说明当前整数对是相连的，则忽略输出，因而需要设计一个数据结构来保存足够的的整数对信息，并用它们来判断一对新对象是否相连。

解决这种问题的数据结构称为并查集。下面我们将介绍4种不同的算法实现，它们均以对象标号为索引的id数组来确定两对象是否处在同一个集合中

7.1 quick-find和quick-union算法

A quick-find算法策略

find操作实现很快速，只需返回对象所在的集合标识；union操作即要遍历整个数组使得p所在的集合分量值都设置为q所在的集合分量值。

• find操作：id[p]不等于id[q],所有和id[q]相等的元素的值变为id[p]的值。find操作只需访问数组一次.
• union操作: 对于每一对输入都要扫描整个数组

quick-find算法的时间复杂度O(N^2),对于最终只能得到少数连通分量的一般应用都是平方级别的

/*p所在的分量标识符，0-N-1*/
int find(int p){
    return id[p];
}

public void union(int p,int q){
    int pId=find(p);
    int qId=find(q);
    if(pId==qId) return ; //已经在同一个分量中，无需采取任何行动

    for(int i=0;i

B quick-union算法策略

union操作很快速，只需将某对象的集合分量标识指向另外一个对象的集合分量，通过父链接的方式表示了一片不相交集合的分量
find操作则需要通过链接的形式找到一个表示它所在集合的标识(p=id[p])

• find操作: 通过链接由一个触点到另外一个触点，知道有个链接它必定指向自身的触点即id[x]=x，该触点必然存在。因而find方法则是通过不断链接遍历到id[x]==x的时为止，该触点为根触点

• union操作: 只需把一个根触点连接到另一个分量的根触点上，通过一条语句就使一个根结点变成另一个根结点的父结点，快速归并了两棵树

它是quick-find方法的一种改良(union操作总是线性级别的)，但并不能保证在所有情况下都比quick-find算法快。quick-union算法的效率取决于树中结点的深度，最坏情况下动态连通性问题只有一个分量，则quick-union的复杂度也是平方级别的。原因: 最坏情况下树的深度为N，树的深度无法得到保证。

public int find(int p){
    while(p!=id[p]) p=id[p];
    return p;
}

public void union(int p,int q){//将p和q所在的集合合并
    int pRoot=find(p);
    int qRoot=find(q);
    if(pRoot==qRoot) return ;
    id[pRoot]=qRoot;
    count--;
}

7.2 加权quick-union算法和使用路径压缩算法

对于quick-union中出现的糟糕算法，我们的改进办法是: 记录每一棵树的大小并总是将较小的树连接到较大的树中，它能够大大改进算法的效率，这种称为加权quick-union。

A 加权quick-union算法策略
较小的树根总是指向较大的树根，使得它构造的树高度远远小于未加权的所有版本的树高度。这里添加的额外数组可以设计成记录分量中结点的个数，也可设计成每个分量的高度。建议使用高度，这种被称为按秩合并(union by rank)的启发式策略，用秩表示结点高度的一个上界，在union操作中具有较小秩的根要指向具有较大秩的根。　

这种加权quick-union算法构造的森林中任意结点的深度最多为lgN，有了它就可以保证能够在合理的时间范围内解决实际中的大规模动态连通性问题，这比简单的算法快数百倍。

...
private int[] sz; //记录每个分量的结点个数
...

public int find(int p){
    while(p!=id[p]) p=id[p];
    return p;
}

/*合并操作总是使小树连接到大树上*/
public void union(int p,int q){
    int pRoot=find(p);
    int qRoot=find(q);

    if(pRoot==qRoot) return;
    if(sz[pRoot]

B 带路径压缩的加权quick-union算法策略

为find添加第一个循环，将查找路径上的每个结点都直接指向根结点，最后得到的结果几乎是完全扁平化的树。注意路径压缩并不改变结点的秩

按算法导论中的平摊分析方法，这种带路径压缩的加权quick-union算法中find、union操作的均摊成本控制在反Ackerman函数的范围内(增长极慢的函数，结果始终控制在4以内的范围)，树的高度一直很小，没有任何昂贵的操作

public int find(int p){ 
        while(p!=id[p]){ 
            id[p]=id[id[p]];
            p=id[p];
        }
        return p;
}

public void union(int p,int q){
        int r1=find(p);
        int r2=find(q);
        
        if(r1==r2) return;
        if(rank[r1]< rank[r2]){
            id[r1]=r2;      
        } else if(rank[r1] > rank[r2]){
            id[r2]=r1;
        } else {
            id[r2]=r1;  //小根指向大根的根结点
            rank[r1]++; //相等时，产生新的高度，根的秩才加1(秩才上升)
        }
        count--;
}

C 总结各种union-find算法的性能特点
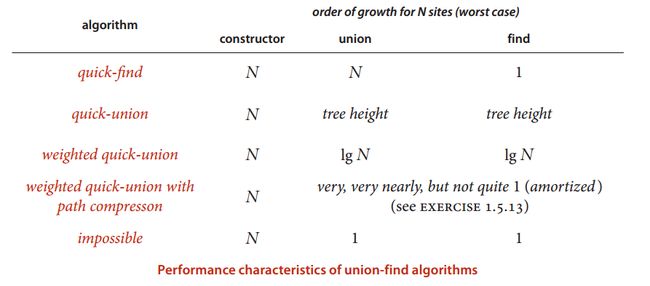
一般地，带路径压缩的加权quick-union算法在解决实际问题时能在常数时间内完成每个操作，性能最好。建议实际应用中使用该算法，它们的比较如下:

具体完整实现如下:

• 用C实现并查集－基于树的双亲表示法

#include "uf.h"
#include 
#include 

/*分配并查集的内存并初始化,n-并查集数组的大小*/
uf_t *uf_alloc(int n){
    uf_t *t=malloc(sizeof(uf_t));
    t->count=n;
    t->id=malloc(n*sizeof(int)); //分配一个连续的堆内存
    int i;
    for(i=0;iid[i]=-1;
    }
    return t;

}

/*释放并查集内存*/
void uf_free(uf_t *t){
    free(t->id);
    free(t);

}

/*查找包含元素p的树的根－集合标号，带路径压缩,并不改变秩*/
int uf_find(uf_t *t,int p){
    int cur=p;
    while(t->id[p] >=0) p=t->id[p]; //找到根结点
    while(cur !=p){ //遍历查找过程的所有结点，将其结点指向根结点
        int temp=t->id[cur];
        t->id[cur]=p;
        cur=temp; 
    }
    return p; 
}

/*合并包含两元素p和q的树集合*/
void uf_union(uf_t *t,int p,int q){
    int r1=uf_find(t,p);
    int r2=uf_find(t,q); //返回的是索引下标，而不是id值

    if(r1==r2) return; //已在同一集合内，无需再合并
    /*id值作为负数时，它的相反数表示该树中结点的个数*/
    if(t->id[r1] > t->id[r2]){ //r2作为根
        t->id[r2] += t->id[r1];
        t->id[r1]=r2;
    } else {
        t->id[r1] += t->id[r2];
        t->id[r2]=r1;
    }
    t->count--;
}

/*返回并查集中不相交集合的分量个数*/
int uf_count(uf_t *t){
    return t->count;

}

/*返回并查集中包含p元素的集合大小*/
int uf_set_size(uf_t *t,int p){
    int root=uf_find(t,p);
    return -t->id[root];
}

• 用Java实现并查集

7.3 应用举例

一般并查集在很多问题中应用广泛，如:

• Percolation（物理系统的渗透）
• Dynamic connectivity（网络中的动态连通性问题）
• Least Common Ancestors（最近公共祖先，Tarjan离线算法）
• Hoshen-Kopelman algorithm in physics
• Kruskal's 最小生成树
• 有限自动机的等价性证明
• Hinley-Milner polymorphic type inference
• Morphological attribute openings and closings

7.3.1 最近公共祖先问题-LCA算法和RMQ算法

7.3.2 求最多连续数子集

给一个整数数组， 找到其中包含最多连续数的子集，比如给：15, 7, 12, 6, 14, 13, 9, 11，则返回: 5:[11, 12, 13, 14, 15] 。最简单的方法是sort然后scan一遍，但是要o(nlgn). 有什么O(n)的方法吗？(http://chuansongme.com/n/93910)

---

8 堆

---

9 海量数据处理的应用

海量数据，一般是指数据量太大，所以导致要么是无法在较短时间内迅速解决，要么是数据太大，无法一次性装入内存，从而导致传统的操作无法实现。一般处理海量数据通常应用到如下数据结构: hash table、trie树、堆、败者树、bitmap和bloom filter

1. hash table通常可用作hash_map或者hash_set,它一般可以用来统计某字符串出现的次数或者将大文件中的元素映射到不同的小文件中
2. trie树除了用于判断字符串的前缀，它还可以统计或排序大量的字符串(不限制于字符串)。
3. 堆一般是用于排序和统计topK的高效数据结构，相比于快速排序的划分算法计算topK，它无需一次性将数据读入内存，特别适合于处理海量数据
4. 败者树和二路归并程序适合将若干有序数组进行归并排序，二路归并比较次数一般为1次，而k路归并的败者树只需要比较k的对数次
5. Bitmap适合判断某关键字是否在集合中，输出重复元素，输出出现几次的数字，处理的文件如果有海量的数据一般结合hash_map将大文件拆分为若干个不同的小文件，再依次处理
6. Bloom filter是一种节省空间的随机化数据结构，是Bitmap的扩展。它在能容忍低错误率的应用场合下，通过极少的错误换取了存储空间的极大节省，在数据库和网络应用中应用非常广泛(具体细节参考后面bitmap的介绍)

---

参考

1. 动态数组的 C 实现
2. Skiplist:A Probabilistic Alternative to Balanced Trees
3. 各种字符串Hash函数比较
4. Which hashing algorithm is best for uniqueness and speed?
5. General Purpose Hash Function Algorithms
6. 精妙的Morris二叉树遍历算法
7. 算法第四版的1.5节案例研究
8. LCA和RMQ问题的转化
9. 教你如何迅速秒杀掉：99%的海量数据处理面试题

---

转载于:https://www.cnblogs.com/xionghj/p/4342807.html