CTR的模型:FM、FFM和DeepFM的理解
参考文献
1.FM系列算法解读(FM+FFM+DeepFM)
2.深入FM和FFM原理与实践
3.CTR学习笔记系列—— FM 和 FFM
4.FM算法及FFM算法
5.『我爱机器学习』FM、FFM与DeepFM
6.CTR预估算法之FM, FFM, DeepFM及实践
7.Rendle, Steffen. “Factorization machines.” Data Mining (ICDM), 2010 IEEE 10th International Conference on. IEEE, 2010.
8.Juan, Yuchin, et al. “Field-aware factorization machines for CTR prediction.” Proceedings of the 10th ACM Conference on Recommender Systems. ACM, 2016.
9.Guo, Huifeng, et al. “Deepfm: A factorization-machine based neural network for CTR prediction.” arXiv preprint arXiv:1703.04247 (2017)
Factorization Machines 学习笔记(一)预测任务
Factorization Machines 学习笔记(二)模型方程
Factorization Machines 学习笔记(三)回归和分类
Factorization Machines 学习笔记(四)学习算法
前言
在计算广告中,CTR是非常重要的一环。对于特征组合来说,业界通用的做法主要有两大类:FM系列和Tree系列。这里我们来介绍一下FM系列。
一、关于FM模型
1.针对的问题:
FM(Factorization Machine)主要是为了解决数据稀疏的情况下,特征怎样组合的问题;
2.FM的解决方法:
核心公式:

其中:
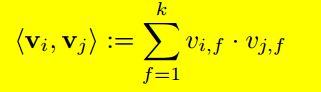
这种属于特征二阶组合表示形式,既包含了单个特征的加权和,也包含了两两特征间的相互关系(即公式的第三项)。
FM特别就特别在第三项。
我们知道,按照直观思维:两两特征间的组合,应该采用 wij 作为两个特征组合的参数,但是这样的话,参数量就会达到 n(n-1)/2,这是很难求的,尤其是数据还是高维稀疏数据的情况下。
wij求解的思路是通过矩阵分解的方法,为了求解wij,我们对每一个特征分量 xi 引入辅助向量 Vi=(vi1,vi2,…,vik)

然后用vivTj对wij进行求解:

(其实说白了就是把 wij 表示成两个向量 vi 和 vj 相乘的形式)
从上式可以看出这样一来,二项式的参数数量由原来的 n(n−1)/2 个减少为 n*k 个 wik,远少于多项式模型的参数数量。
另外,参数因子化使得 xhxi 的参数和 xhxj 的参数不再相互独立,因为有了 xh 特征关联。因此我们可以在样本稀疏的情况下相对合理地估计FM的二次项参数。具体来说, xhxi 和 xhxj 的系数分别为
好,上面的改进表示完成了,那么怎么求解V呢??先对上面目标函数里的第三部分做一个拆分化简处理:

这个化简是很简单的,化简之后的目标函数如下,FM的二次项化简为只与 vi,f 有关的等式。因此FM可以在线性时间对新样本做出预测,复杂度和LR模型一样,且效果提升不少。(时间复杂度达到O(kn))

接下来就可以采用SGD来训练得到 V 的值:

∑nj=1 vj,fxj 只与 f 有关,只要求出一次所有的 f 元素,就能够计算出所有 vi,f 的梯度,而 f 是矩阵V中的元素,计算复杂度为O(kn)。当已知 ∑nj=1 vj,fxj 时计算每个参数梯度的复杂度是O(1),更新每个参数的复杂度为O(1),因此训练FM模型的复杂度也是O(kn)
附:FM和SVM的主要区别
【1】SVM的二元特征交叉参数是独立的,而FM的二元特征交叉参数是两个k维的向量vi、vj,交叉参数就不是独立的,而是相互影响的;
【2】FM可以在原始形式下进行优化学习,而基于kernel的非线性SVM通常需要在对偶形式下进行;
【3】FM的模型预测是与训练样本独立,而SVM则与部分训练样本有关,即支持向量;
【4】为什么线性SVM在和多项式SVM在稀疏条件下效果会比较差呢?
线性SVM只有一维特征,不能挖掘深层次的组合特征在实际预测中并没有很好的表现;
而多项式SVM正如前面提到的,交叉的多个特征需要在训练集上共现才能被学习到,否则该对应的参数就为0,这样对于测试集上的case而言这样的特征就失去了意义,因此在稀疏条件下,SVM表现并不能让人满意。
而FM不一样,通过向量化的交叉,可以学习到不同特征之间的交互,进行提取到更深层次的抽象意义。
个人理解:
本质上FM就是把显示的两两特征间的相关系数wij,转化为一种向量乘积表示的形式,通过学习这种特征的表示向量,使得学到的特征间关系不仅仅是显示表示的部分,而且包含更为深刻的关联性;与此同时,这种学习方法,也更为适合高维稀疏数据场景,因为这种表示向量并不依靠具体的两两特征数据样本来学习,而是可以通过现有关联的两两特征间的数据来学习,通过这种间接的方式,摆脱了相关系数的学习依赖具体两两特征的局限性,因此具有很好的效果。
二、关于FFM模型
1.针对的问题:
我们知道,在FM模型中,每个特征只用一个隐向量来学习和其它特征的潜在影响,虽然这种表示挖掘到了两两特征之间的关联性,但是考虑实际应用场景中,不同特征之间的影响关系是不一样的,比如广告商对于广告主的影响和广告商对用户的影响就并不能等同看待,因此FM模型这种表示形式和实际的表示需求之间就会出现矛盾。
2.FFM模型的解决方法:
考虑到问题所在,于是FFM模型将field概念引入FM模型。field是什么呢?可以理解为一种分类,即相同性质的特征放在一个field。 比如EPSN、NBC都是属于广告商field的,Nike、Adidas都是属于广告主field,Male、Female都是属于性别field的。简单的说,同一个类别特征进行one-hot编码后生成的数值特征都可以放在同一个field中。如果是数值特征而非类别,可以直接作为一个field。
通过引入field的概念,2阶多项式模型、FM模型和FFM模型之间的比较如下图:
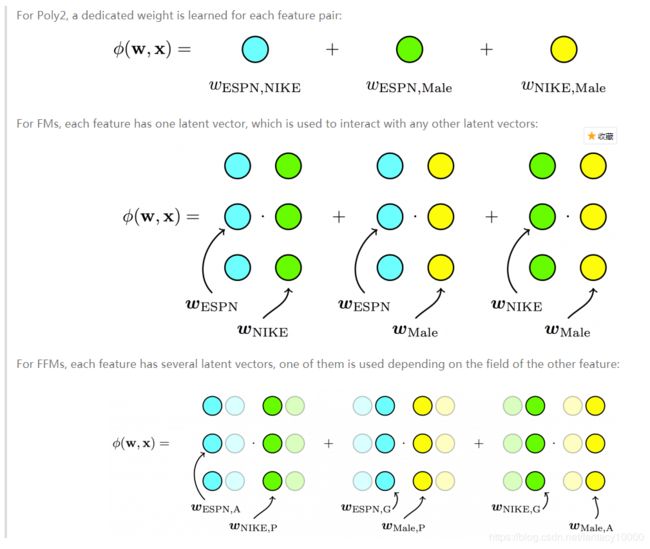
引入field之后的FFM数学公式表示为:
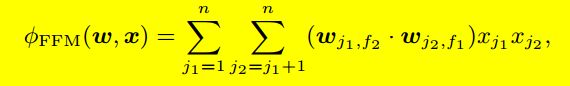
其中 fi 和 fj 分别代表第 i 个特征和第 j 个特征所属的field。若field有 f 个,隐向量的长度为 k,则二次项系数共有 dfk 个,远多于FM模型的 dk 个。此外,隐向量和field相关,并不能像FM模型一样将二次项化简,计算的复杂度是 d2k。
通常情况下,每个隐向量只需要学习特定field的表示,所以有 kFFM≪kFM。
3.W的学习过程:
4.具体实现的部分trick:
【1】梯度的分步计算,通过共用部分梯度计算结果,减少重复计算;
【2】考虑FFM对于训练参数的敏感性,FFM的学习率是随迭代次数变化的,具体的是采用AdaGrad算法;
【3】采用OpenMP多核并行计算,采用SSE3指令并行编程;
【4】要使用FFM模型,特征需要转化为“field_id:feature_id:value”格式,相比LibSVM的格式多了field_id,即特征所属的field的编号,feature_id是特征编号,value为特征的值;
【5】样本归一化。FFM默认是进行样本数据的归一化的 。若不进行归一化,很容易造成数据inf溢出,进而引起梯度计算的nan错误。因此,样本层面的数据是推荐进行归一化的;
【6】特征归一化;
【7】省略零值特征。从FFM模型的表达式可以看出,零值特征对模型完全没有贡献。包含零值特征的一次项和组合项均为零,对于训练模型参数或者目标值预估是没有作用的。因此,可以省去零值特征,提高FFM模型训练和预测的速度,这也是稀疏样本采用FFM的显著优势;
三、关于DeepFM模型
1.针对的问题:
从论文表述来看,本质上FM系列模型目的都是挖掘特征间的关系,尽管FM模型理论上可以得到高阶特征关系,但是实际应用中一般只采用二阶特征,因为复杂度太高,现有的FNN、PNN和Wide&Deep模型都有着预训练耗时以及需要特征工程等方面的问题,
因此DeepFM针对的问题就是:如何找到一种可以很好兼顾低阶和高阶特征,并且无需特征工程和预训练的方法???
2.DeepFM模型的解决方法:
总体结构把握:FM和DNN的结合(输入一致,embedding)
上图左边就是FM模型的神经网络表示,而右边的则为Deep部分,为全连接的网络,用于挖掘高阶的交叉特征。整个模型共享embedding层,最后的结果就是把FM部分和DNN的部分做sigmoid:
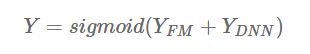
【1】FM部分:

step1:模型输入是一个d维向量,其中第 i 维即为第 i 个 field 的特征表示,如果是类别,则为one-hot编码后的向量,连续值则为它本身。
step2:然后对每个field分别进行embedding:
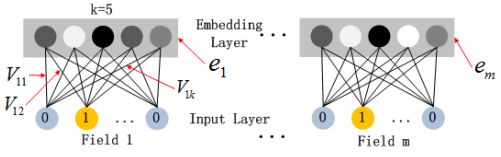
值得注意的是,即使各个field的维度是不一样的,但是它们embedding后长度均为k。
step3:接着FM层即为embedding后结果的内积和一次项的和,最后一层sigmoid后再输出结果。
embedding的目的在于通过这种表示,使得和FM模型等价!!!
解释:
假设第 i 个 field 向量维度为k,embedding层的参数可以表示为一个k * m的矩阵:

其中 vab 可以理解为第a个取值embedding后的结果在隐向量的第b维。由于进行了one-hot编码,所以对应的xfiledi~只有一个值为1,其余的都为0,假设第c列为1,则:

若两个field做内积,假设非0的那一列为c和d则:
![]()
其实和FM模型是一样的。
【2】Deep部分:
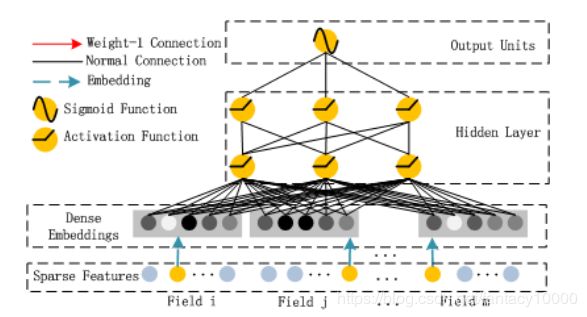
Deep部分就是一个前向传播神经网络,输入也是embeddig后的向量;
附:
类似于FFM对于FM模型来说,划分了field,对于不同的field内积时采用对应的隐向量。同样可以把DeepFM进行进化为DeepFFM,即将每一个field embedding为m个维度为k的隐向量(m为field的个数)


