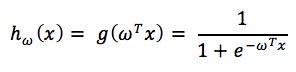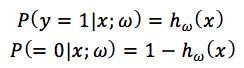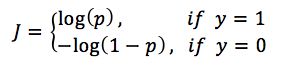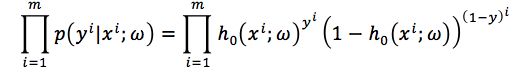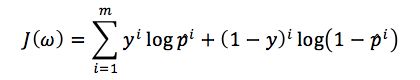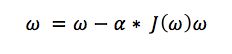逻辑回归
摘要:逻辑回归主要解决分类,利用sigmoid 函数 转化为区间(0,1) 可用来语音识别,图像识别等识别方面,也可用来广告点击。
1. 定义
给定一些数据点,它们分别属于两个不同的类,现在要找到一个线性分类器把这些数据分成两类。如果用x表示数据点,用y表示类别(y可以取1或者-1,分别代表两个不同的类),一个线性分类器的学习目标便是要在n维的数据空间中找到一个超平面(hyper plane),这个超平面的方程可以表示为( ωT中的T代表转置):
![]()
可能有小伙伴对类别取1或-1有疑问,事实上,这个1或-1的分类标准起源于logistic回归。
Logistic回归目的是从特征学习出一个0/1分类模型,而这个模型是将特性的线性组合作为自变量,由于自变量的取值范围是负无穷到正无穷。因此,使用logistic函数(或称作sigmoid函数)将自变量映射到(0,1)上,映射后的值被认为是属于y=1的概率。
假设函数
其中x是n维特征向量,函数g就是logistic函数。
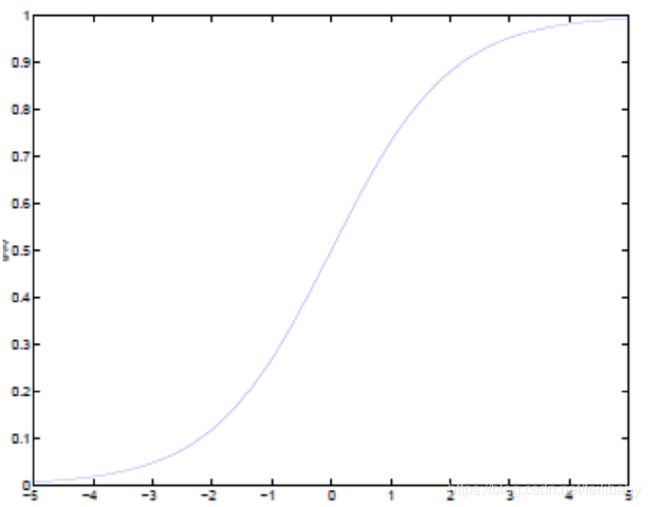
而
的图像是
可以看到,将无穷映射到了(0,1)。
而假设函数就是特征属于y=1的概率。
从而,当我们要判别一个新来的特征属于哪个类时,只需求hωx即可,若 hωx大于0.5就是y=1的类,反之属于y=0类。
2. 损失函数
2.1 损失函数定义
逻辑回归和线性回归最大的区别就是:逻辑回归解决的是分类问题,得到的y要么是1,要么是0。而我们估计出来的p是概率,通过概率决定估计出来的p到底是1还是0。因此,也可以将损失函数分成两类:
如果给定样本的真实类别y=1,则估计出来的概率p越小,损失函数越大(估计错误)
如果给定样本的真实类别y=0,则估计出来的概率p越大,损失函数越大(估计错误)
那么将用什么样的函数表示这两种情况呢,可以使用如下函数:
辑回归的模型为h0x;ω ,假设现在有样本{xi, yi},其中xi表示样本的特征,yi∈{0,1}表示样本的分类真实值,yi=1的概率是pi,则yi=0的概率是1−pi,那么观测概率为:
则最大似然函数为:
对这个似然函数取对数之后就会得到的表达式
实际操作中一般会加个负号改为求最小. 估计这个J(ω)的极大值就可以得到ω的估计值。
逻辑回归的损失函数不是定义出来的,而是根据最大似然估计推导出来的。
2.2 损失函数优化
求解损失函数最小问题就变成了这个最大似然函数的最优化问题,这里通常会采样随机梯度下降法(SGD)和拟牛顿迭代法来进行优化(牛顿法使用了二阶梯度,梯度下降仅仅是一阶梯度)。
- 梯度下降法
由于LR的损失函数为:
这样就变成了求min(Jω)
其中α为步长,直到Jω不能再小时停止
梯度下降法的最大问题就是会陷入局部最优,并且每次在对当前样本计算cost的时候都需要去遍历全部样本才能得到cost值,这样计算速度就会慢很多(虽然在计算的时候可以转为矩阵乘法去更新整个ω值)
- 随机梯度下降法
现在好多框架(mahout)中一般使用随机梯度下降法,它在计算cost的时候只计算当前的代价,最终cost是在全部样本迭代一遍之求和得出,还有他在更新当前的参数w的时候并不是依次遍历样本,而是从所有的样本中随机选择一条进行计算,它方法收敛速度快(一般是使用最大迭代次数),并且还可以避免局部最优,并且还很容易并行(使用参数服务器的方式进行并行)
这里SGD可以改进的地方就是使用动态的步长
![]()
- 其他优化方法
- 拟牛顿法(使用Hessian矩阵和cholesky分解)
- BFGS
- L-BFGS
优缺点:无需选择学习率α,更快,但是更复杂。
3. 过拟合
如果我们有很多的特性,在训练集上拟合得很好,但是在预测集上却达不到这种效果
- 减少feature个数(人工定义留多少个feature、算法选取这些feature)
- 正则化(为了方便求解,L2使用较多) 添加正则化之后的损失函数为:
4. 多分类
关于LR的多分类,一般采用softmax。 假设离散型随机变量y的取值集合是1,2,..,k,输出当前样本下属于哪一类的概率,并且满足全部概率加起来=1
关于softmax和k个LR的选择
如果类别之间是否互斥(比如音乐只能属于古典音乐、乡村音乐、摇滚月的一种)就用softmax;如果类别之前有联系(比如一首歌曲可能有影视原声,也可能包含人声,或者是舞曲),这个时候使用k个LR更为合适。
5. LR优缺点
5.1 优点
- 实现简单;
- 分类时计算量非常小,速度很快,存储资源低;
5.2缺点
- 容易欠拟合,一般准确度不太高;
- 只能处理两分类问题(在此基础上衍生出来的softmax可以用于多分类),且必须线性可分(用一个线性函数可以将两类样本完全分开);