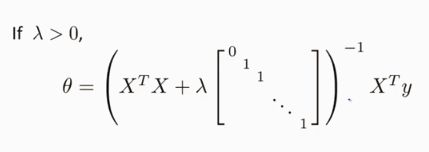深度学习、机器学习、tensorflow学习笔记杂烩,更新……
2019.3.16
最近看了一些机器学习的视频和python深度学习的书籍,但最后还是发现直接看tensorflow框架的书来得直白。以下主要是书中的一些要点记录。
0、张量:在tensorflow中所有的数据都通过张量表示,张量可以理解为多维数组。0阶张量为标量,就是一个数;1阶张量为向量;n阶张量为n维数组。张量主要由3个属性:名字(name)、维度(shape)、类型(type)
1、神经网络参数:输入数据(特征值)的权重,神经网络优化的过程其实就是优化神经元参数取值的过程。
2、神经网络训练:其实就是设置参数的过程,即不断地运行程序,优化参数,使得输出值和预期值差距越来越小。
3、输入层和输出层之间的神经网络就是隐藏层,一般一个神经网络隐藏层越多,则神经网络越深。
4、前向传播和反向传播:
前向传播法:由输入(实体中的特征向量)、神经网络连接结构(不同神经元之间的连接关系)、参数(神经元连接边上的权重)。从神经网络输入层开始,通过和参数一起运算到达下一层,下一层再和参数一个运算,最后直到输出。
输入层到输出层之间运算一般是:输入层向量和输出层之间的参数(权重)做矩阵乘法,加上一个偏置项得到。
反向传播法:每次训练迭代,会基于预测值和真实值之间的差距更新参数的取值,使得预测结果和真实答案更加接近,从而优化模型。可以根据定义好的损失函数优化神经网络中参数的取值,从而使神经网络模型在训练数据集上的损失达到一个较小值。
梯度下降:参数的梯度是该点的偏导。会以迭代的方式更新参数,不断朝着梯度的反方向让参数朝着总损失更小的方向更新。但只有当损失函数为凸函数时,梯度下降算法才能保证达到全局最优解。
学习率:优化函数中定义每次参数更新的幅度,不能太大或太小。
损失函数:用来计算当前预测值和真实答案之间的差距,然后通过反向传播算法来调整神经网络参数的取值使得差距可以被缩小。cross_entropy定义了真实值和预测值之间的交叉熵。也叫代价函数
优化函数:反向传播优化神经网络参数的函数。定义了优化函数后,可以使损失函数变小。
激活函数:其实就是对每个神经元的输出通过一个非线性函数处理,使得整个神经网络模型不再是线性的了。
偏置项:如果没有偏置项,分类时只能在空间里画经过原点的直线或平面。
过拟合:当模型过于复杂(使用了过多的特征)后,可以对训练集有很好的识别效果,但是对新的预测集效果不佳,因为记录了训练数据中过多的噪音。也就是过拟合试图完全拟合训练数据,从而导致模型无法泛化到全新的样本,无法预测新的样本数据。
正则化:避免过拟合的方式是正则化,在损失函数中加入刻画模型复杂程度的指标,通过限制权重的大小,使得模型不能任意拟合训练数据中的噪音。正则化有一个权重值(参数),代表复杂损失在总损失中的比例。
滑动平均模型:使测试数据更加健壮。会对每一个变量维护一个影子变量,每次运行变量更新时,影子变量也会更新。
5、矩阵乘法:使用tf.matmul完成。但是交叉熵中的乘法直接时对应元素之间相乘即可。矩阵点积:矩阵中对应元素乘积之和。
6、图片在张量中保存方式:例如28*28像素的图片,可以保存在一个长度为784的一维数组中,每一个元素取值范围为[0,1],0表示白色背景,1表示黑色背景,代表了颜色的深浅。如果有n张图片进行训练的话,也就是输入数据就是n个样本,每个样本都包含了这784个特征。每个样本的每个特征都会对应一个权重值。
3.18卷积神经网络
1、过滤器或者内核:可以将当前层神经网络上的一个子节点矩阵转化为下一次神经网络上的一个单位节点矩阵。其过程就是通过将一个过滤器从神经网络当前层的左上角移到右下角,并且在移动中计算每一个对应的单位矩阵得到。这个过滤器也类似于前向传播法中的参数。
2、卷积层的参数个数和图片的大小无关:它只和过滤器的尺寸、深度以及当前层(输入层)的节点矩阵的深度有关。
3、池化层:将一张分辨率较高的图片转化为分辨率较低的图片,缩小全连接层中节点的个数,从而达到减少整个神经网络中参数的目的。
4、全连接层:经过多轮的卷积层和池化层处理后,在卷积神经网络的最后一般会是由1-2个全连接层来给出最后的分类结果。卷积层和池化层可以看成自动图像特征提取的过程,特征提取完成后,依然要使用全连接层完成分类任务。
经典卷积神经网络模型:LeNet5模型,Inception模型,两者在卷积层连接方式和过滤器大小方面不一样。
3.22
1、tf.placeholder:相当于定义了一个位置,这个位置中的数据在程序运行中再指定,这样在程序中就不需要生成大量的常量来提供输入数据
,而只需要通过placeholder传入tensorflow计算图。
Tensorflow的设计理念称之为计算流图,在编写程序时,首先构筑整个系统的graph,代码并不会直接生效,这一点和python的其他数值计算库(如Numpy等)不同,graph为静态的,类似于docker中的镜像。然后,在实际的运行时,启动一个session,程序才会真正的运行。这样做的好处就是:避免反复地切换底层程序实际运行的上下文,tensorflow帮你优化整个系统的代码。我们知道,很多python程序的底层为C语言或者其他语言,执行一行脚本,就要切换一次,是有成本的,tensorflow通过计算流图的方式,帮你优化整个session需要执行的代码,还是很有优势的。
所以placeholder()函数是在神经网络构建graph的时候在模型中的占位,此时并没有把要输入的数据传入模型,它只会分配必要的内存。等建立session,在会话中,运行模型的时候通过feed_dict()函数向占位符喂入数据。
3.27Keras和TensorFlow的关系
TensorFlow是最著名的用于深度学习生产环境的框架。它有一个非常大非常棒的社区。然而,TensorFlow的使用不那么简单。另一方面,Keras是在TensorFlow基础上构建的高层API,比TF(TensorFlow的缩写)要易用很多。
Keras的底层库使用Theano或TensorFlow,这两个库也称为Keras的后端。无论是Theano还是TensorFlow,都是一个“符号式”的库。
3.30 吴恩达视频中的一些要点
偏导数和导数:导数,是对含有一个自变量的函数进行求导。偏导数,是对含有两个自变量的函数中的一个自变量求导。
导数和偏导没有本质区别,都是当自变量的变化量趋于0时,函数值的变化量与自变量变化量比值的极限。一元函数,一个y对应一个x,导数只有一个。二元函数,一个z对应一个x和一个y,那就有两个导数了,一个是z对x的导数,一个是z对y的导数,称之为偏导。导数=0处,一般是最小或者最大值。
梯度下降和学习率: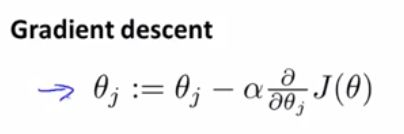 使用学习率a*代价函数在参数theta附近的偏导数来更新参数的值,从而希望找到一个(或者一批)参数theta值使代价函数最小,这个过程就是梯度下降。一般是通过不停地迭代才能实现,学习率描述的事参数更新的幅度。
使用学习率a*代价函数在参数theta附近的偏导数来更新参数的值,从而希望找到一个(或者一批)参数theta值使代价函数最小,这个过程就是梯度下降。一般是通过不停地迭代才能实现,学习率描述的事参数更新的幅度。
如何确定学习率:
如图所示,学习率太高,有可能在代价最小两边徘徊,也可能一下子冲过最小值处。如果太小,则可能导致梯度下降太慢,迭代次数过多。
特征缩放:为了使梯度下降算法快速收敛(代价函数不再变化,不再减小),减少迭代的次数,一般把特征的值缩放到在[-1,1]之间,或者在这附近。
矩阵的逆运算: A是一个方阵(行=列),只有方阵有逆运算。不存在逆矩阵的矩阵是奇异矩阵,例如全零构成的矩阵。
A是一个方阵(行=列),只有方阵有逆运算。不存在逆矩阵的矩阵是奇异矩阵,例如全零构成的矩阵。
I是一个单位矩阵:在矩阵的乘法中,有一种矩阵起着特殊的作用,如同数的乘法中的1,这种矩阵被称为单位矩阵。它是个方阵,从左上角到右下角的对角线(称为主对角线)上的元素均为1。除此以外全都为0。
3.31吴恩达视频
1、logistic回归(sigmod函数):
A.线性回归处理的是数值问题,也就是最后预测出的结果是数字,例如房价。
B.逻辑回归属于分类算法,也就是说,逻辑回归预测结果是离散的分类,例如判断这封邮件是否是垃圾邮件,以及用户是否会点击此广告等等。
是一种解决分类问题非常强大、广泛的算法,通常和sigmoid函数是一样的: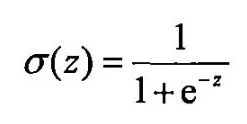 ,他将输出限定在[0,1]之间,进行分类。hθ(x)的作用是, 对于给定的输入变量, 根据选择的参数计算输出变量=1 的可能性。
,他将输出限定在[0,1]之间,进行分类。hθ(x)的作用是, 对于给定的输入变量, 根据选择的参数计算输出变量=1 的可能性。 ,
,
4.1 吴恩达视频
3、正则化:为了降低模型的过拟合,而对参数进行正则化处理;其实就是在迭代过程中,通过调整参数,把某些特征的作用弱化或者丢弃。
4、SVM:也是一种监督学习算法。
支持向量机(support vector machines)是一种二分类模型,它的目的是寻找一个超平面来对样本进行分割,分割的原则是间隔最大化,最终转化为一个凸二次规划问题来求解。由简至繁的模型包括:
当训练样本线性可分时,通过硬间隔最大化,学习一个线性可分支持向量机;
当训练样本近似线性可分时,通过软间隔最大化,学习一个线性支持向量机;
当训练样本线性不可分时,通过核技巧和软间隔最大化,学习一个非线性支持向量机;
非线性,是指SVM擅长应付样本数据线性不可分的情况,主要通过松弛变量(也有人叫惩罚变量)和核函数技术来实现,这一部分是SVM的精髓。
范数:
||w||是什么符号?||w||叫做向量w的范数,范数是对向量长度的一种度量。我们常说的向量长度其实指的是它的2-范数,范数最一般的表示形式为p-范数,可以写成如下表达式
向量w=(w1, w2, w3,…… wn)
它的p-范数为
p=2的时候,||w||就是传统的向量长度。当我们不指明p的时候,就像||w||这样使用时,就意味着我们不关心p的值,用几范数都可以;
参考解析几何公式:
两条直线间的距离公式:设两条直线方程为Ax+By+C1=0,Ax+By+C2=0,d=|C1-C2|/√(A^2+B^2)
点到直线的距离公式:直线Ax+By+C=0 坐标(Xo,Yo)那么这点到这直线的距离就为: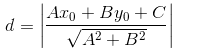
阈值:临界值。
可以使用软件包libsvm进行svm相关的操作,而不需要手动去数学运算。
5、对偶问题:每一个线性规划问题都伴随有另一个线性规划问题,称为对偶问题。原来的线性规划问题则称为原始线性规划问题,简称原始问题。
6、无监督学习:聚类算法,常用的有K-means,K均值法。
4.11重看logistic回归一章视频后理解: sigmod函数 中的Z代表原来的回归函数,由于回归函数输出的值是离散的,其范围是无限的,但是把Z经过sigmod函数处理后,结果只输出一个范围在[0,1]之间的结果。当Z>=0时,g(z)>=0.5,就认为是正类,用y=1表示;当Z<0时,则g(z)<0.5,就认为是负类,用y=0表示。从而把回归问题转化为了分类问题,实现了对样本的分类。
(y = 1或0)
梯度下降和学习率: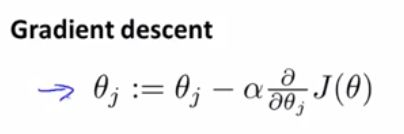 使用学习率a*代价函数在参数theta附近的偏导数来更新参数的值,从而希望找到一个(或者一批)参数theta值使代价函数最小,这个过程就是梯度下降。一般是通过不停地迭代才能实现,学习率描述的事参数更新的幅度。
使用学习率a*代价函数在参数theta附近的偏导数来更新参数的值,从而希望找到一个(或者一批)参数theta值使代价函数最小,这个过程就是梯度下降。一般是通过不停地迭代才能实现,学习率描述的事参数更新的幅度。
线性回归和logistic回归的梯度下降算法看起来相同,但其实h(x)所代表的函数是不同的:蓝色是线性回归线性函数,红色是logistic回归sigmod函数
2、决策边界:在边界的两侧或者内外,把样本分成不同的类别;决定决策边界的是假设本身(所选择用来拟合训练集的函数)以及参数(各特征的参数)数值。
3、除了梯度下降优化算法,还有一些更高级、更复杂的优化算法。如共轭梯度
4、多元分类:将样本分为多个类别,将概率最高的类别作为分类。实现思路:当需要把样本分成n个类别时,可先把要分类的看成正类,则其他样本看成负类,共通过n次二分法完成分类,如下所示。
4.12
1、求线性回归方程正规数学方程上的方法是用最小二乘法,最小二乘法”的思想是这样的,假设我们拟合出的直线代表数据的真实值,而观测到的数据代表拥有误差的值。为了尽可能减小误差的影响,需要求解一条直线使所有误差的平方和最小。最小二乘法将最优问题转化为求函数极值问题。函数极值在数学上我们一般会采用求导数为0的方法。也就是先建立假设函数:如 y = ax + b,将实际值Yi与计算值Yj(Yj=a0+a1Xi的离差(Yi-Yj)的平方和: 为 最小为“优化判据”。然后构造函数
为 最小为“优化判据”。然后构造函数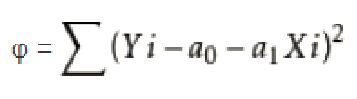 ,分别对a0, a1求偏导,即可得到其极值。但求偏导的做法并不适合计算机,可能求解不出来,也可能计算量太大。所以一般采用梯度下降的算法。
,分别对a0, a1求偏导,即可得到其极值。但求偏导的做法并不适合计算机,可能求解不出来,也可能计算量太大。所以一般采用梯度下降的算法。
2、线性回归梯度下降。
(1)先确定线性回归假设方程,和代价函数J。求出使代价函数J最小时的参数θ即可确定回归函数h。
代价函数J是采用了平方误差代价函数,这是对大多数问题特别是回归中比较常用的选择。
 (假设函数;参数;代价函数;目标方程;目的:求代价函数最小值时,对应的参数值,即可确定最佳的h方程)
(假设函数;参数;代价函数;目标方程;目的:求代价函数最小值时,对应的参数值,即可确定最佳的h方程)
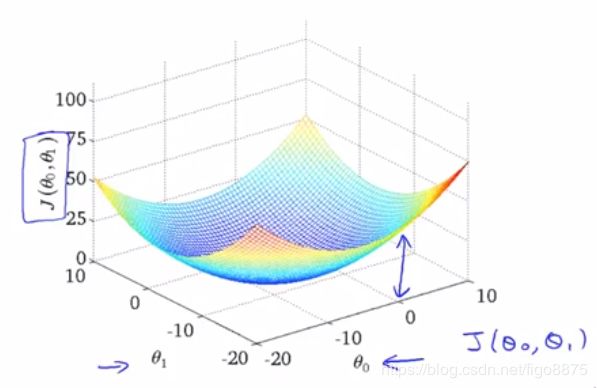 (代价函数的形状:θ1和θ2组成两个坐标轴,J(θ1,θ2)是高度,当θ1,θ2变化时,优化函数J的值发生变化。)
(代价函数的形状:θ1和θ2组成两个坐标轴,J(θ1,θ2)是高度,当θ1,θ2变化时,优化函数J的值发生变化。)
 (高线图:由于代价是3D的,可用右边高线图来在二维平面表示,其中相同颜色的圆形具有相同的θ1,θ2值,左边会有对应的参数假设函数h)
(高线图:由于代价是3D的,可用右边高线图来在二维平面表示,其中相同颜色的圆形具有相同的θ1,θ2值,左边会有对应的参数假设函数h)
(2)分别求各参数在代价函数J中的偏导数,通过θ - 一个学习率α*偏导数来重复迭代更新θ的值: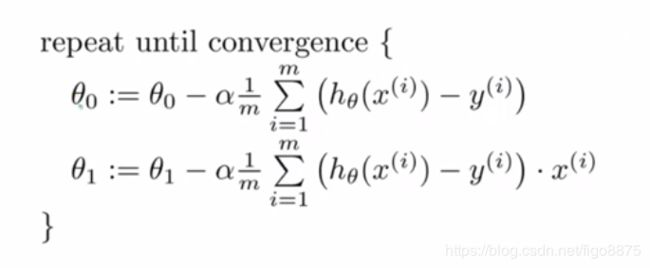
(3)通过给参数θ0,θ1...θn设置初值,通过一点点地改变参数的值,从而求得代价函数的最优值,也就是取得局部最低点的值时的各参数值,即可求出最终的线性回归方程。(可看吴恩达机器学习单变量线性回归课时10)
 temp是记录参数θ在小幅变动时的临时变量。α是学习率,
temp是记录参数θ在小幅变动时的临时变量。α是学习率,![]() 是代价函数J在θj附近的偏导数,两者相乘就是变化的幅度。
是代价函数J在θj附近的偏导数,两者相乘就是变化的幅度。
2、即便学习率α是固定的,随着一点点地向局部最优值移动,由于斜率变小,导数项会越来越小,因此θ更新速度也会越来越慢,最终在局部最优值处J(θ)基本会停止变化,达到收敛。(课时11)
3、 凸函数:只有全局最优解,没有局部最优解。
4、batch梯度下降:每一步梯度下降都会遍历所有的训练样本,因此每次的代价函数值为所有样本的总和。
4.17
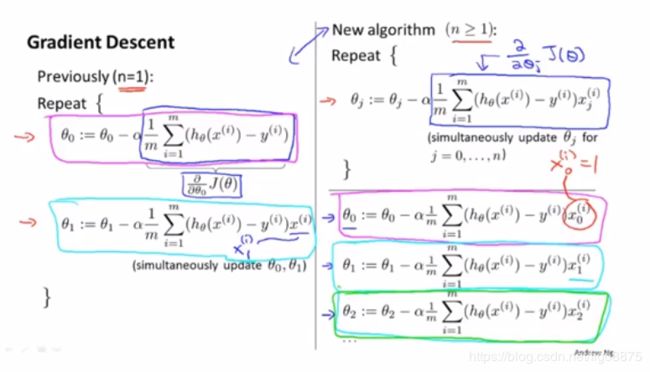
多元梯度下降
上图左边是只含两个参数的梯度下降,右边是包含多个参数的梯度下降,即同步地更新每个参数的值。(课时29)
特征缩放:多个参数意味着特征数量很多,不同特征的取值可能相差特别大,这样会导致参数和代价函数之间关系的图像比较不友好,也会影响梯度下降的收敛效率。所以,这时候要确保所有特征都处在一个相近的范围。于是会用到特征缩放,一般把特征转化为[-1, 1]之间,并不是必须是这个范围,只要大致相近的值也可以。如下图所示:(课时30)
 如图所示,左边没有使用缩放,x1和x2取值相差较大,导致图形很瘦长,影响梯度下降时收敛速度;而右边把X1和X2缩放到[0,1]之间(特征值除以取值范围长度),最终参数和代价函数的高线图像就很圆。
如图所示,左边没有使用缩放,x1和x2取值相差较大,导致图形很瘦长,影响梯度下降时收敛速度;而右边把X1和X2缩放到[0,1]之间(特征值除以取值范围长度),最终参数和代价函数的高线图像就很圆。
多元梯度下降的学习率a:学习率不能太大或太小,太小可能收敛太慢,太大可能错过最佳值。
特征选择:在多参数的问题中,如何选择特征很重要,也很困难。
正规方程:区别于迭代方法的直接求解线性方程参数的解法。当特征数目不大时,可以采用正规方程法,但并不适用于一些复杂的算法,如逻辑回归。(课时33)使用正规方阵求解参数公式如下:x是特征向量,y是目标值向量。
4.18 正则化
过拟合:当你的模型过于复杂时,比如使用了过多的特征,但是训练集却比较小时,可能会导致模型对训练集完美拟合,但是对新样本预测效果不佳,这就是过拟合了。 因此,为了避免过拟合,一种方式是需要对部分特征进行丢弃,只选择特定的特征(用人工或模型选择)。另一种方式就是正则化。
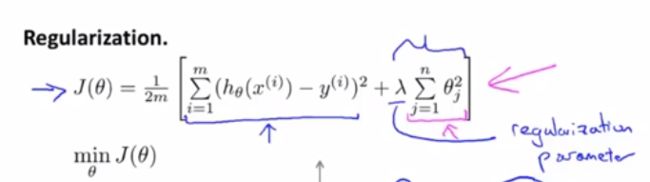
正则化会保留所有的特征变量,但是会对部分特征进行“惩罚“,也就是减小特征的量级,让他们趋向于0,最终简化这个模型。表达时如下,也就是在代价函数加上一个正则项。对每个参数都进行正则化处理,要使代价函数最小,就是既要使正则项最小,也要使方差项最小,正则项最小意味着接近0,也就是丢弃特征,而在该特征取多小的值得同时让方差项也最小,两者达到某种平衡时就是正则化的目标。
线性回归正则化:而在正则化的线性回归梯度下降中,参数迭代时的变化形式变成如下:(课时57)
正则化在逻辑回归中运用:
代价函数变为:
梯度下降时参数变化也会加上正则项。
4.20神经网络
当对一些图像方面进行识别时,所含的特征数非常庞大,导数参数个数非常多,那么线性回归或者逻辑回归无法解决这样的问题,而神经网络可以减少参数。(课时63)
神经网络术语:
权重是指参数;偏置项是指X0,始终为1.
激活项:一个具体的神经元通过权重矩阵计算,并使用激活函数处理后输出的值
激活函数:是一个非线性函数,主要是可以在把神经元计算结果进行非线性化处理
隐藏层是看不见的,可以有多个。多个隐藏的为深度学习。
前向传播:方向为从输入层,激活---隐藏层,激活---输出层,激活
4.23 神经网络解决非线性回归问题案例
以图形识别为例,先把图像也就是像素点通过输入层输入神经网络,并通过第一个隐藏层计算出一系列特征,再通过下一个隐藏层计算出更复杂的特征,这样一层层地通过隐藏层计算出更复杂的特征,最后通过最后一层(全连接层)的逻辑分类器来进行预测 。
神经网络实现多分类:
例如要识别的结果有四种:行人、汽车、摩托、卡车,原来一般有y= 1,2,3,4表示,而在神经网络中使用向量表示,对应序号的位置为1表示该分类的目标值、其次,该神经网络模型最后将有四个逻辑回归分类器,分别预测对应位置为真的概率。