概率校准 Probability Calibration
对于二分类分类器,除了得到AUC评价指标,常还需要了解分类器预测概率的准确性。比如分类器预测某个样本属于正类的概率是0.8,那么就应当说明有80%的把握认为该样本属于正类,或者100个概率为0.8的里面有80个确实属于正类。根据这个关系,可以用测试数据得到Probability Calibration curves。
假设我们考虑这样的一种情况:在二分类中,属于类别0的概率为0.500001,属于类别1的概率为0.499999。假若按照0.5作为判别标准,那么毋庸置疑应该划分到类别0里面,但是这个真正的分类却应该是1。如果我们不再做其他处理,那么这个就属于错误分类,降低了算法的准确性。如果在不改变整体算法的情况下,我们是否能够做一些补救呢?或者说验证下当前算法已经是最优的了呢?这个时候就用到了概率校准。
Brier分数
这部分摘自:概率校准与Brier分数
Brier分数是衡量概率校准的一个参数。
简单来说,Brier分数可以被认为是对一组概率预测的“校准”的量度,或者称为“ 成本函数 ”,这一组概率对应的情况必须互斥,并且概率之和必须为1。 Brier分数对于一组预测值越低,预测校准越好。
引用维基百科的一个例子说明 Brier分数的计算方式:
假设一个人预测在某一天会下雨的概率P,则Brier分数计算如下:
如果预测为100%(P = 1),并且下雨,则Brier Score为0,可达到最佳分数。
如果预测为100%(P = 1),但是不下雨,则Brier Score为1,可达到最差分数。
如果预测为70%(P = 0.70),并且下雨,则Brier评分为(0.70-1)2 = 0.09。
如果预测为30%(P = 0.30),并且下雨,则Brier评分为(0.30-1)2 = 0.49。
如果预测为50%(P = 0.50),则Brier分数为(0.50-1)2 =(0.50-0)2 = 0.25,无论是否下雨。
概率校准就是对分类函数做出的分类预测概率重新进行计算,并且计算Brier分数,然后依据Brier分数的大小判断对初始预测结果是支持还是反对。
常用模型的表现
这部分大多来自sklearn官网。
精确校准的分类器是概率分类器, 其可以将 predict_proba 方法的输出直接解释为 confidence level(置信度级别). 例如,一个经过良好校准的(二元的)分类器应该对样本进行分类, 使得在给出一个接近 0.8 的 prediction_proba 值的样本中, 大约 80% 实际上属于正类. 以下图表比较了校准不同分类器的概率预测的良好程度:
第一张图是概率校准曲线,说明实际概率与预测概率的关系。可见Logistic回归预测概率比较准(模型本身的特点),朴素贝叶斯过于自信(可能由于冗余特征所致,违背了特征独立性前提)呈反sigmoid曲线,SVM很不自信呈sigmoid曲线,随机森林也是。
第二张图是预测概率分布图,Logistic和朴素贝叶斯大多分布在0或1附近,都是比较自信的,而随机森林多分布在0.2或0.8附近,SVM很不自信主要分布在0.5附近。
概率校准
常用的概率校准方法有2个:基于Platt的sigmoid校准、isotonic回归法。
sigmoid校准适用于sigmoid形状的情况(SVM就是典型),但对于其他形状的校准效果差(如朴素贝叶斯)。
isotonic校准使用于任何情况。
sklearn中的实现:sklearn.calibration.CalibratedClassifierCV
主要参数:
base_estimator :初始分类函数
method :校准采用的方法。取值‘sigmoid’ 或者 ‘isotonic’
cv :交叉验证的折叠次数。
另外,在sklearn中,SVC中设置"probability=True"就可以获得预测概率,其本质就是通过sigmoid校准得到的,如果没有设置这个参数则得到的概率是S形不自信的。
校准实例
这部分摘录自sklearn官网举例。
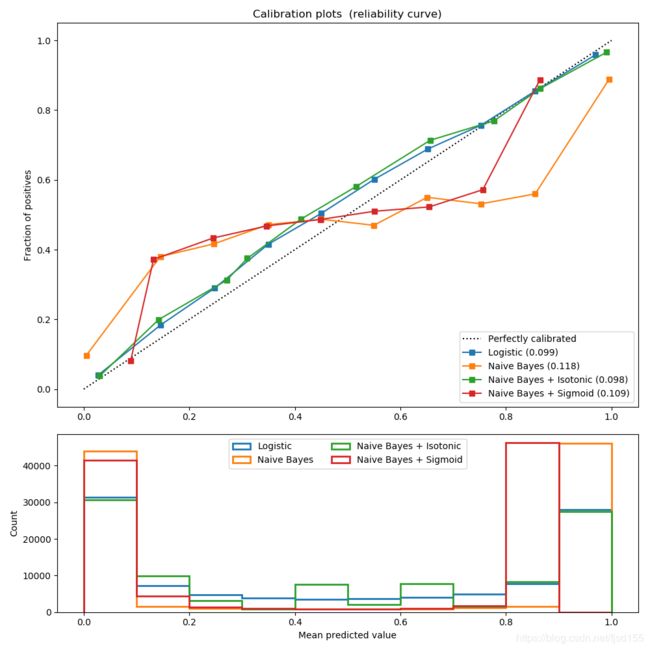
The experiment is performed on an artificial dataset for binary classification with 100,000 samples (1,000 of them are used for model fitting) with 20 features. Of the 20 features, only 2 are informative and 10 are redundant. The first figure shows the estimated probabilities obtained with logistic regression, Gaussian naive Bayes, and Gaussian naive Bayes with both isotonic calibration and sigmoid calibration. The calibration performance is evaluated with Brier score, reported in the legend (the smaller the better). One can observe here that logistic regression is well calibrated while raw Gaussian naive Bayes performs very badly. This is because of the redundant features which violate the assumption of feature-independence and result in an overly confident classifier, which is indicated by the typical transposed-sigmoid curve.
Calibration of the probabilities of Gaussian naive Bayes with isotonic regression can fix this issue as can be seen from the nearly diagonal calibration curve. Sigmoid calibration also improves the brier score slightly, albeit not as strongly as the non-parametric isotonic regression. This can be attributed to the fact that we have plenty of calibration data such that the greater flexibility of the non-parametric model can be exploited.
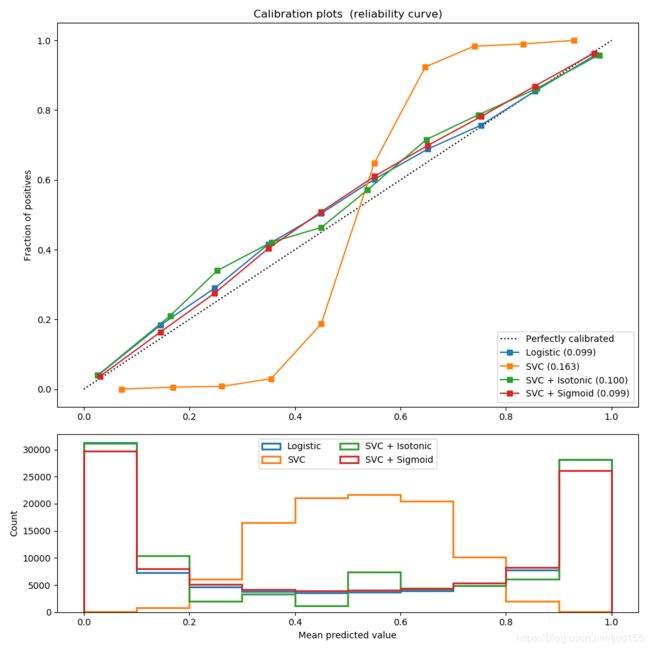
The second figure shows the calibration curve of a linear support-vector classifier (LinearSVC). LinearSVC shows the opposite behavior as Gaussian naive Bayes: the calibration curve has a sigmoid curve, which is typical for an under-confident classifier. In the case of LinearSVC, this is caused by the margin property of the hinge loss, which lets the model focus on hard samples that are close to the decision boundary (the support vectors).
Both kinds of calibration can fix this issue and yield nearly identical results. This shows that sigmoid calibration can deal with situations where the calibration curve of the base classifier is sigmoid (e.g., for LinearSVC) but not where it is transposed-sigmoid (e.g., Gaussian naive Bayes).
参考文献:
sklearn官方文档
概率校准与Brier分数
概率校准 - 监督学习 - 用户指南