第2章：基础知识——《知识图谱概念与技术》肖仰华

2.1 概述

知识图谱与知识表示的关系：

知识图谱狭义概念是一类语义网络，语义网络只是各种知识表示中的一种。

知识图谱与自然语言处理关系密切，体现在：

1. 知识提取的一个重要途径是从自由文本中抽取，而文本信息抽取是自然语言处理的核心问题之一。
2. 知识图谱构建好之后通常可以用作支撑自然语言理解的背景知识。

知识图谱与数据库的关系：

知识图谱在构建好之后和进入应用之前还需要实现对图谱数据的高效管理，包括语义丰富的查询表达、高效的查询处理、系统化友好的图谱数据管理等。

知识图谱与机器学习的关系：

在知识图谱应用的整个生命中周期中，多个环节都与机器学习有关。

知识图谱与计算机子学科（知识表示、自然语言处理、数据库、机器学习）关系如下图所示。

除了与计算机各子学科有着较强的关联外，知识图谱与语言学以及认知科学等学科也有密切的关联。

2.2 知识表示

2.2.1 基本概念

知识必须经过合理的表示才能被计算机处理。知识表示是对现实世界的一种抽象（Abstract）表达。评价知识表示的两个重要因素是：

• 表达能力（Expressiveness）
• 计算效率（Efficiency）

知识的表示方式主要分为符号表示和数值表示。在实际应用中，根据不同的学科背景，人们发展了基于图论、逻辑学、概率论的各种知识表示。

• 语义网络、知识图谱、RDF（Resource Description Framework）、实体关系图等均是基于图的知识表示。

• 逻辑学产生了包括一阶谓词逻辑以及产生式规则在内的知识表示。

• 将概率论引进基于图论和逻辑学的知识表示，发展出了概率图模型及概率软逻辑等。

• 在图论、概率论与逻辑学的交叉领域又进一步发展出了马尔科夫逻辑网。

基于不同学科发展出来的知识表示如下图所示：

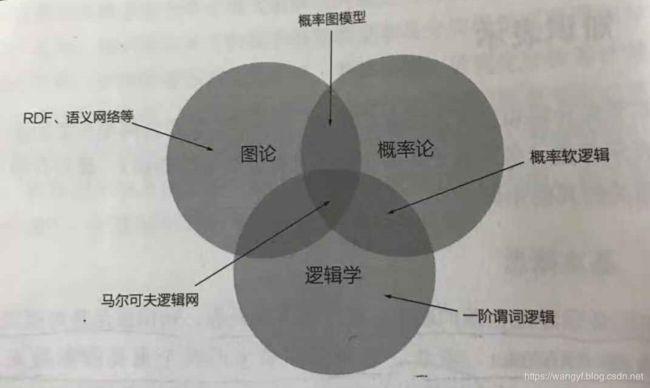
知识图谱较为常见的表示方式是基于图的表示方式。为了能让计算机有效地处理和利用知识图谱，还需要有知识图谱的数值化表示。

2.2.2 知识图谱的图表示

1. 基于图的表示

图在可视化时，通常用原点表示节点，用线表示节点之间的关系，如下图（a）所示。图的另一种表示形式是邻接矩阵（Adjacency Matrix），如下图（b）所示。

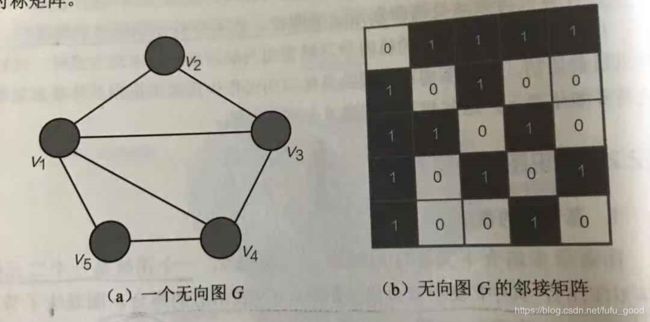
2. 基于三元组的表示

RDF是用于描述现实中资源的W3C标准，他说描述信息的一种通用方法，使信息能被计算机应用程序读取并且理解。

每个资源的一个属性及属性值，或者它与其他资源的一条关系，都可以表示成三元组，其形式如下：

• 主体（Subject）、谓词（Predicate）及客体（Object）。如：<亚里士多德，isA，科学家>
• 主体（Subject）、属性（Property）及属性值（Property Value）。如：<亚里士多德，出生地，Chalcis>

利用这些属性和关系，大量资源就能被连接起来，形成一个大规模RDF知识图谱数据集。因此，一个知识图谱可以视作三元组的集合。示例如下图：

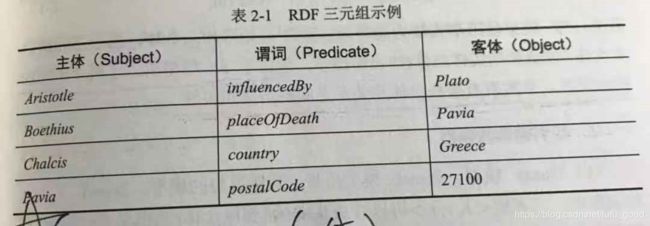
2.2.3 知识图谱的数值表示

基本的思路是将知识图谱中的点和边表示成数值化的向量。不同的向量表示在实际应用中有着不同的效果，如何为知识图谱中的实体与关系求得最优的向量化表示，是当前知识图谱表示学习所关注的核心问题。

学习实体和关系的向量化表示的关键是，合理定义知识图谱中关于事实（即三元组）的损失函数fr(h,t)，其中h和t是三元组的两个实体h和t的向量化表示。在通常情况下，当事实成立时，我们期望fr(h,t)最小。在建立相应优化目标之后，通常使用SGD（Stochastic Gradient Descent，随机梯度下降）等算法学习模型中的相关参数。

1. 基于距离的模型

其代表模型是SE。基本思想是当两个实体属于同一个三元组时，它们的向量表示在投影空间中也应该彼此靠近。因此，定义损失函数为向量投影后的距离：
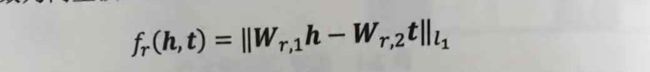其中，SE模型使用形式较为简单的1-范式。矩阵Wr,1和Wr,2用于三元组头实体向量h和尾实体向量t的投影操作。

2. 基于翻译的模型

（1）TransE模型。TransE模型是基于翻译思想的模型。TransE认为在知识库中，三元组可以看成头实体h和尾实体t利用关系r所进行的翻译。条件是使h+r≈t，其损失函数如下：

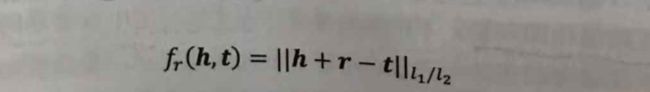
其基本思路如下图所示：

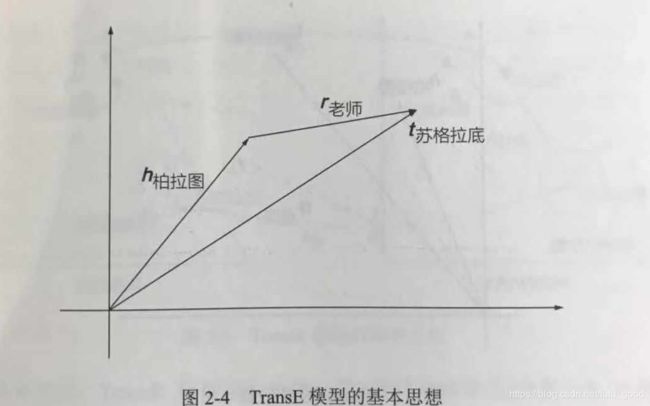
（2）TransH模型。TransE模型中的h+r≈t假设太强，导致在自反、一对多、多对一等关系下实体向量学习的错误。比如，对于自反关系r，和同时成立，导致h=t。

为了解决上述问题，TransH模型放宽了h+r≈t这一严格假设，只要求头尾实体和关系r相对应的超平面上的投影彼此接近即可。其基本思路如下图：

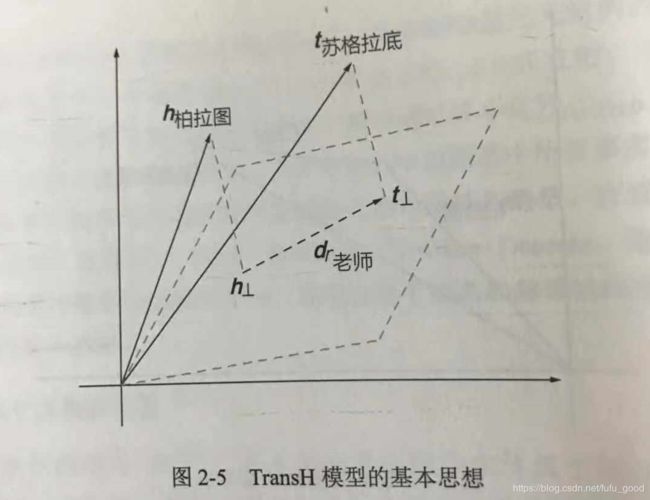
（3）TransR模型。在TransE模型和TransH模型中，实体和关系都在相同的空间中进行表示。这种做法无法区别两个语义相近的实体在某些特定方面（关系）上的不同。因此，TransR模型提出为每个关系构造相应的向量空间，将实体与关系在不同的向量空间中分开表示。其思想如下图所示：

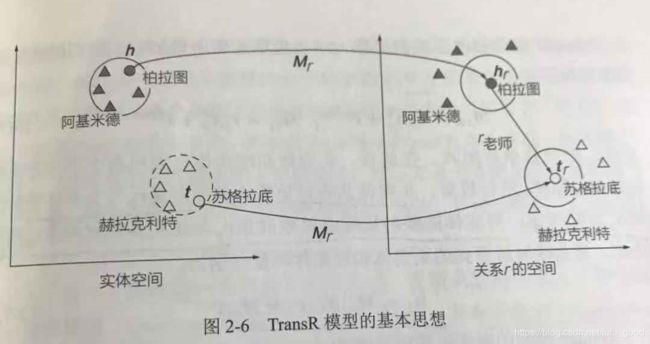
（4）TransD模型。TransD模型认为映射函数应与实体、关系同时相关。其基本思想如下图：

2.2.4 其他相关知识表示

1. 逻辑谓词

命题是一个非真即假的陈述。命题可以通过谓词来表示，谓词的一般形式是P(x1,x2,…,xn)。其中，P是谓词的名称，xi是谓词的项。xi既可以是常量也可以是变量。

在谓词前还可以将否定、析取、合取、蕴含、等价操作构成符合命题。

为了进行一步刻画谓词和个体之间的关系，在谓词逻辑中引入了：全称量词和存在量词。

2. 产生式规则

产生式规则常用于表示事实与规则，以及相应的不确定性度量。产生式规则是一种形如“条件-动作”的规则，基本形式如下：IF <条件> Then <结果>

产生式规则与逻辑蕴含有着相同的基本形式，但是在语义上，逻辑蕴含P=>Q只能表达如果命题P为真则Q一定为真。产生式规则后件不仅可以为命题，还可以是动作。

3. 框架

框架表示是以框架理论为基础发展起来的一种结构化的知识表示。

框架是一种描述所论对象（事物、时间或概念）属性的数据结构。其基本结构和示例如下图：

4. 树形知识表示

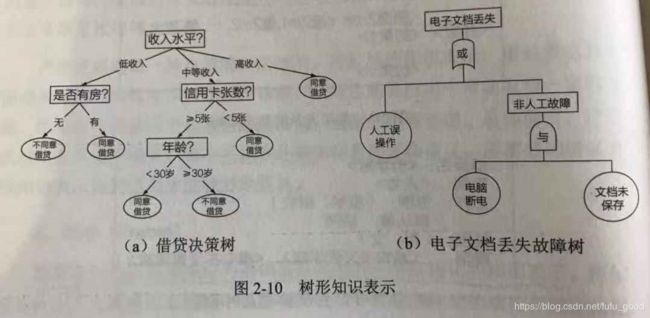
树形知识表示可以用于表达复杂条件组合下的决策与动作。决策树就是典型的树形知识表示。其根节点和中间节点对应一个属性，相应属性分类的样本集合被划入对应的子节点。叶节点表示最终的分类结果。其例子如下图（a）所示。

另一类常见的树形知识表示是故障树。故障树是一种树形的逻辑因果关系图。在故障树中，父节点是产生故障的结果，也称为输出事件；子节点是产生故障的原因，也称为输入事件。为了能够表达因果逻辑关系，故障树利用逻辑符号（“与”、“或”）连接子节点和父节点。其例子如下图（b）所示。

5. 概率模型（Probalistic Graphical Model）

贝叶斯网络，也被称为信念网络或者有向无环图模型，是一种概率图模型，也是不确定知识表示的典型方法。一个贝叶斯网络就是一个有向无环图，其中节点是一组随机变量X={X1,X2,…,Xn}，节点之间的有向边（由父节点指向子节点）代表随机变量之间的影响。

每个随机变量Xi仅依赖于其父亲节点集Parent(Xi），其例子如下图：

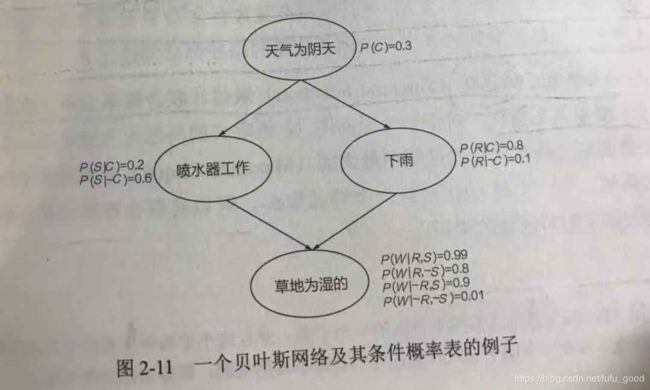
贝叶斯网络的两个基本问题是学习和推理。学习是指如何从数据中习得最优的贝叶斯网络模型。推理是指给定贝叶斯网络和其中一些随机变量的取值设置，推断其他随机变量分布。

贝叶斯网络的优点：

• 能够准确表达决策过程中的不确定性。
• 能够有效的将专家的先验知识与数据驱动的学习方法进行融合。

有向概率图模型的简化版本是无向概率图模型，又被称作马尔科夫随机场（Markov Random Field，MRF）。

6. 马尔科夫随机链（Markov Chain，MC）

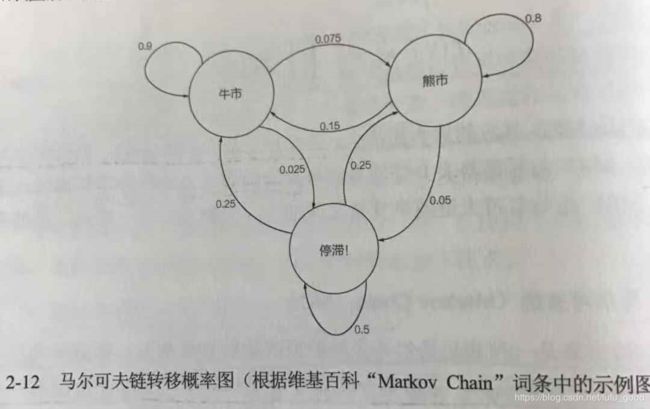
马儿可夫链是一种满足马儿可夫性离散随机变量集合。所谓的马儿可夫性（Markov Property），是指某个随机变量序列的下一个状态仅仅与当前的状态有关，而与之前的状态没有关系。其例子如下图所示。

7. 马尔可夫逻辑网

马尔可夫逻辑网（Markov Logic Network，MLN）是将一阶逻辑和马尔可夫随机场结合起来的模型。一个典型的MLN如下图所示：

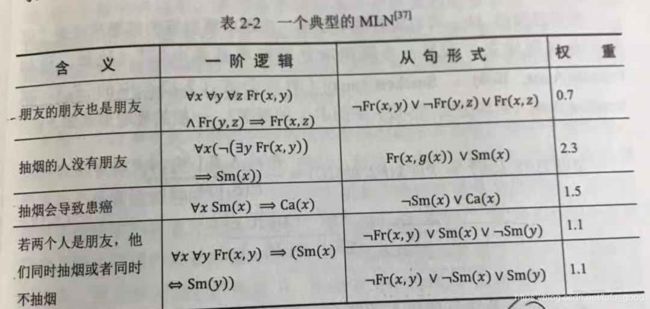
MLN可以视作定义具体的MRF（马尔可夫随机场）的模板。

2.3 机器学习

机器学习（Machine Learing）是一种刚从观察数据（样本）中寻找规律，并且学习到的规律（模型）对未知或无法观测数据进行预测的方法。

2.3.1 机器学习的基本概念

每一个样本数据中的观测数据均需要有合理的表示才能被计算机有效处理，这种表示被称为特征（Feature）。选择特征是使用机器学习解决问题的重要步骤，即设计者需要确定选择数据中哪些信息来表示样本。

机器学习的基本任务就行学习一个最优的预测函数F:X->Y，我们期望模型具有较强的泛化能力，也就是说从训练集上习得的模型在未见的测试集上也能取得较好的预测结果。提升机器学习的泛化能力是机器学习的核心任务。

在统计学习中通过以下两点提升机器学习的泛化能力：

• 专家总有一定的关于预测模型的先验知识。因此可以预先设定目标所在的范围，也就是设定模型函数的函数族。
• 需要设计评测指标以评估不同参数下模型的优劣。一个直接的想法是，设计一个损失函数，用于度量函数f的预测误差。

一般而言，机器学习模式的损失函数都是可导的，因此最小化损失函数的优化问题可以使用梯度下降法进行求解。

机器学习的三个关键要素如下：

• 模型选择，也就是预测函数F
• 优化准则，也就是设计的损失函数
• 优化方法，也就是优化问题求解过程

根据训练集中每个样本的标签是否已知分为：

• 监督学习。训练集中每个样本的标签都是已知的。
• 半监督学习。训练集中包含少量的标注数据和大量未标注数据。
• 无监督学习。训练集中每个样本数据的都没有标注。

2.3.2 深度学习概述

传统机器学习的局限性较为集中的体现在以下两点：

• 传统机器学习中的样本特征主要靠专家经验或特征转换的方法来获取。
• 传统机器学习一般只能使用较为简单的函数形式（比如线性函数）表达模型，而而模型的表达能力对于机器学习的效果来说至关重要，简单的模型难以表达复杂的函数映射。

深度学习的出现一定程度上弥补、突破了浅层学习的上述局限性。深度学习是指基于深度神经网络的一类机器学习模型。深度神经网络在传统浅层神经网络的基础上引入了更多的中间层，因而是具有较深层次的神经网络模型。一个深度神经网络由输入层——中间层——输出层的机构构成，其中间层本质上完成了自动特征提取。深度神经网络一方面降低了专家定义特征的代价，另一方面可以捕捉隐性特征，其在图像、语音、文件等数据的特征提取中往往能取得较好的效果。此外，引入多个中间层的深度神经网络可以表达复杂的非线性函数映射。深度神经网络示意图如下图所示。

从函数的学习角度来看，深度学习通过复合多个简单函数来构造复杂函数，模型所需训练参数由每个简单函数中的参数组成，即：
$$y=F(x)=F_L(...F_3(F_2(F_1(x))))$$
这样一个L层的函数可以将输入的底层特征x经由$F_1、F_2......$多次转换，产生深度的特征表示，并最终实现从输入到输出的复杂映射（在大多数情况下都是非线性映射）。

深度学习中常见的函数形式是带激活函数的全连接层，即$F_i(x)=\sigma (Ax+B)$，这里的$\sigma$可以选择tanh或Sigmoid等多种非线性函数。

深度学习网络有各种架构——从简单的线性模型到卷积神经网络——不同的深度神经网络模型都可以视作从输入数据学习有效特征表示的过程。而特征学习得关系在于，用有限的参数表达有效的特征。

2.3.3 卷积神经网络（CNN）

卷积神经网络是一类以卷积层（使用卷积操作代替全连接层所使用的的矩阵乘法操作）作为网络的基本元素的深度神经网络，一般常用于处理图像数据。

以图像处理为例，全连接神经网络模型有两个弊端：

• 参数太多，更容易产生过拟合。
• 没有使用局部不变性。

卷积层的引入的CNN的根本特征。卷积层使用一个相对于原始数据而言规模很小的卷积核（有时又叫做过滤器）作为参数。卷积操作如下图所示，因此卷积操作能显著降低表示的复杂性。在CNN的卷积层之后，往往还跟着一个池化层。池化层使用池化操作进一步降低表示的复杂性。

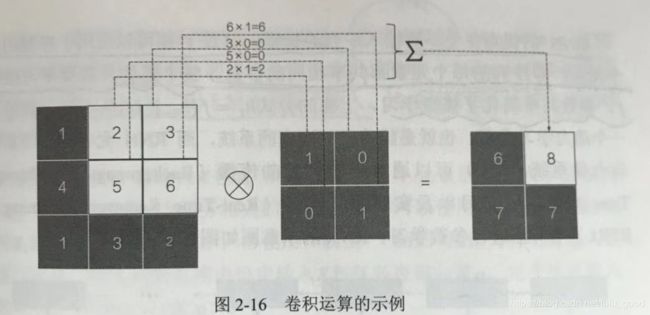
CNN的结构通常由输入、卷积层、池化层以及全连接层构成。CNN模型的特点是稀疏连接、参数共享。此外，CNN中的卷积运算以及池化操作能够实现对于图像处理所需特定变换（比如平移）的不变性。

2.3.4 循环神经网络（RNN）

循环神经网络（Recurrent Neural Network，RNN）是一类专门用于处理序列数据的神经网络。RNN得以实例化的根本原因也在于参数共享。RNN利用序列数据的性质实现了序列上不同时间点的权重共享。因此，它使用了一类特殊的函数来代替全连接层，大大减少了参数量，同时也使模型更好的利用序列性质。RNN中的“循环”本质上是指数据在t时刻的状态取决于其前序序列，这在语音与文本数据处理中是必要的。

给定一个输入序列$x_{1:T}=(x_1,x_2,...,x_T)$，循环神经网络通过公式$h_t=f(h_{t-1},x_t)$更新带反馈边的隐藏层参数。在这种情况下，RNN处理序列的当前元素时充分考虑了序列中前序状态中的元素。隐藏单元$h_{i-1}$被称作记忆或状态，它是由序列的前$i-1$个元素生成的。

RNN的优点在于不管输入序列的长短，函数$f$都可以应用于序列的每个元素，即序列的每个元素都共享相同的参数。RNN示意图如下：

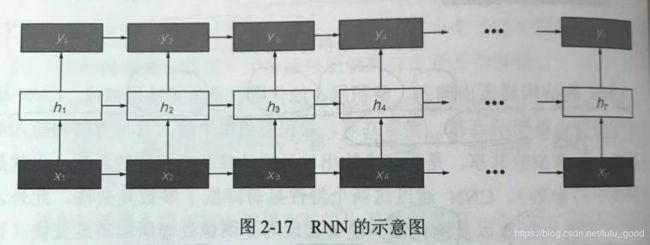
2.3.5 注意力机制

在深度神经网络中引入注意力机制，使模型每一阶段的输出只需要根据输入的某些片段进行计算，而无需处理整个输入。

2.4 自然语言处理（NLP）

自然语言处理（Natural Language Processing，NLP）的主要使命是自然语言的理解和生成。

2.4.1 基本概念

文本是知识图谱的数据来源，我们需要对其中的语句做各种处理。NLP可以在词法分析（Lexical Analysis）、语法分析（Syntactic Analysis）、语义分析（Semantic Analysis）以及语用分析（Pragmatic Analysis）等层面进行展开。NLP常见任务如下图所示。

• 断句一般通过标点符号。
• 分词是指对文本进行词汇的切割。
• 词性标识是给句子中的每个词标记相应的词性。
• 词形还原是指将某一单词还原至原型。
• 对于分析任务来说起噪音作用的被称为停用词。
• 依存句法分析旨在识别句子的语法结构。
• 命名实体识别是识别句子的词序列中具有特定意义的实体，并将其标注为人名、机构名、日期、地名、时间和职位等类别的任务。
• 共指消解旨在识别句子中同一个实体的不同表述。
• 语义角色表述是将句子中的某些词或短词标注为给定语义角色的过程。

2.4.2 文本的向量表示

1.离散表示

独热表示：在语料库中，为每个词做一个索引编码，根据索引编码进行表示。比如，针对“I love you”为每个词做索引编码。假设带索引编码的字典为{“I”:1,“love”:2,“you”:3}，那么每个单词的独热表示为：
$$I:[1,0,0]$$$$love:[0,1,0]$$$$you:[0,0,1]$$
词袋表示：词袋表示常用于文本表示，直接将文本中单词的独热向量相加即可。比如上面的例句，其词袋表示为$[1,1,1]$。

2. 连续表示

连续表示则可以更好的捕捉词与词之间的语义关系。连续表示形式最常用的是分布式表示。分布式表示的思想是将语言的语义或语法特征分散存储在一个低维、稠密的实数向量中。分布式的向量往往通过建立自然语言的预测模型学习而得。代表性模型有Word2Vec的Skip-gram模型。

Skip-gram模型的基本思想是习得合理词向量，使得利用词向量准确预测上下文的概率尽可能高。