描述性统计部分（一）----统计量

描述性统计部分（一）—-统计量

标签（空格分隔）： 概率论与数理统计

---

1、期望 E(X)

又叫均值、加权算术平均值，其计算公式为：

E(X)=∑ni=1xin=∑ji=1xi⋅ki∑ji=1ki=∑i=1∞xi⋅pi=∫∞−∞x⋅f(x)dx=∑i=1∞g(yi)⋅pi=∫∞−∞g(y)⋅f(x)dx

式中各参数含义：

参数	含义
E(X)	期望值 ，代表随机变量的平均水平，常用 x¯ （样本）、 μ （总体）来表示
xi	各数据的值，如得分、身高等等观测值
n	随机变量的个数，样本常用 n ，总体常用 N
ki	随机变量的分组内个数，比如气枪比赛中，在汇总数据时会说，有5个10环，4个9环，1个8环，它等价于10、10、10、10、10、9、9、9、9、8，此时就可以使用 ki 来表示5、4、1，来计算其期望（均值）
pi	当 n 趋向于很大时， Kin 就等价于 pi ，如上例中共有10个数，5个10环，就可以表示为 pi=50% 的得分为10环
f(x)	当随机变量为连续型变量时的概率密度表示式，即上面的 pi
yi	x=g(y) 时，可以直接使用 x 的概率密度来计算 y 的期望，离散型变量时使用和式（倒数第二个），连续型变量时，使用积分公式（倒数第一个）

具有的性质如下

性质	条件
E(C)=C	C为常数
E(CX)=CE(X)	C为常数
E(X+Y)=E(X)+E(Y)	XY为两个随机变量，可以推广到无限个随机变量相加
E(X⋅Y)=E(X)⋅E(Y)	XY为两个互相独立的随机变量，可以推广到无限个独立随机变量之积

基本应用1
1、描述随机的均值情况，表明随机变量的集中趋势;
2、利用期望计算式及求导公式求期望极值，当 ddxE(X)=0 时取得极值(一元二次方程或在某个取值区间的高次方程)

2、方差 D(X) &标准差 σ(X)

其计算公式为：

D(X)=E{[X−E(X)]2}=∑k=1∞[xk−E(X)]2pk=∫∞−∞[xk−E(X)]2f(x)dx=E(X2)−[E(X)]2

标准差，也叫均方差：

σ(X)=D(X)−−−−−√

式中各参数含义：

参数	含义
D(X)	方差，代表着随机变量与期望的偏离程度，也可以写为 Var(X) ，但因使用平方去负数，存在两个缺陷，一是与随机变量的单位不一致（单位的平方），二是对极值非常敏感，所以引入标准差来更好地解决这两个问题
σ(X)	如上所述，为解决方差的单位及敏感性而设置的一个统计量，比方差的应用范围更广
k	随机变量个数
pk	随机变量的概率，此处及下面的 f(x) 可以把方差实际理解为一个 Y=g(x)=X−E(X) 的随机变量的期望
f(x)	当随机变量为连续型变量时的概率密度表示式，即上面的 pi
E(X2)&[E(X)]2	即各随机变量的”平方的期望”及”期望的平方”

具有的性质如下

性质	条件
D(C)=0	C为常数
D(CX)=C2D(X);D(X+C)=D(X)	C为常数
D(X+Y)=D(X)+D(Y)+2E{(X−E(X))(Y−E(Y))}	XY为两个随机变量
D(X+Y)=D(X)+D(Y)	XY为两个互相独立的随机变量，可以推广到无限个独立随机变量之和

基本应用（同上）
描述随机变量的分布情况，离散性（或偏离性）情况;

3、其它统计量

偏度、峰度
偏度：数据集不对称的程度。越接近0，对称性越好，注意，对称并不代表就是正态！当偏度大于0时，为右偏，峰值靠左，尾部向右，当偏度小于0时，峰值靠右，尾部向左。

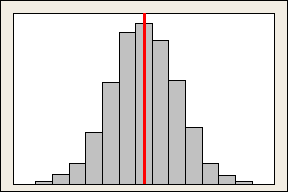
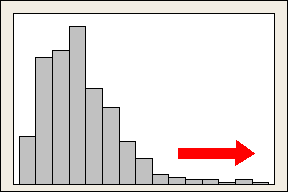
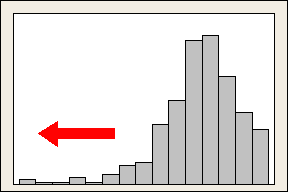
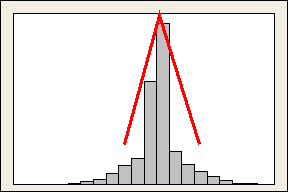
峰度：数据集达到峰值的程度。其值为与正态相比，若峰值高于正态则为正，图形越尖；低于则为负，图形越平坦。

样本平均值、样本方差、样本标准差、样本k阶矩、样本k阶中心距
样本平均值： X¯¯¯=1n∑ni=1Xi
样本方差： S2=1n−1∑ni=1(Xi−X¯)2
样本标准差： S=S2−−√=∑ni=1(Xi−X¯)2n−1−−−−−−−−−√
样本k阶(原点)矩： Ak=1n∑ni=1Xki,k=1,2,3,……
样本k阶中心矩： Bk=1n∑ni=1(Xi−X¯)k,k=1,2,3,……

均值的标准误、变异系数
均值标准误(SE Mean)：度量样本均值多大精确程度地估计总体均值，并用于创建总体均值的置信区间。它等于样本标准差 (s) 除以样本数量 (n) 的平方根。
变异系数(COV)：一种相对变异性的度量，等于标准差除以均值。因为它是一个无量纲数，所以可以用来比较均值显著不同的总体的离散性。

最小值(Min)、最大值(Max)、极差、总和
顾名思义，就是一组随机变量中的最小值及最大值，而极差=最大值-最小值，总和就是所有数据相加

中位数(M)、众数、下四分位数(Q1)、上四分位数(Q3)、P分位数、四分位间距
中位数：把随机变量按顺序排列之后，有N个大于它，有N个小于它。如果随机变量的个数为奇数个，则排列之后中间的数为中位数，若为偶数个，则为中间两个数的算术平均数。与均值相比，中位数对极值并不敏感，因此，它通常更能代表偏斜数据的中心点。
众数：随机变量中出现最多的一个数。
上下四分位数：下四分位，即有25%的数小于它的数，上四分位，有75%的数小于它的数。
P分位数：有np个数小于它，有n(1-p)个数大于它。上下四分位、中位数属于P分位数的特殊值，计算公式如下：

xp={x([xp]+1),12[x(np)+x(np+1)],当np不是整数当n是整数

四分位间距(IQR)： IQR=上四分位数-下四分位数=Q3-Q1
注：由最小值、下四分位数、中位数、上四分位数、最大值五个数可以画出箱线图，同时，通常以双侧大于1.5IQR作为异常值的判断，去掉异常值之后，再做箱线图，称为修正箱线图。

N缺失数，N非缺失数，N合计
即随机变量中，所观测到的缺失值数、非缺失值数及观测值总数。缺失数不包含实际值，N合计则指N缺失+N非缺失，比如发出邮件调查问卷100份，返回80份，则缺失20份，此20份无数据，为N缺失数，80份为N非缺失数，N合计为100份。

累积N、百分比、累积百分比
累积N： 即为某个单边区域（如 <、>、≤、≥ 等)的分组，累计有多少个，比如10个人，有2个身高150cm，3个160cm，5个170cm，则累积N的分组方式为 ≤ 150、 ≤ 160、 ≤ 170，此时累积N分别为2,5,10.
百分比： 即为各分组数量除以总数量， n/N∗100
累积百分比： 与累积N类似，把个数换成百分比即可。通常用来制作Parto控制图。

---

1. 只显示对于本度量值或统计量的本身应用，其对于分布及推断统计的应用于后续再讨论。 ↩