二分查找(Binary Search) 常见问题解决方法总结
缘由
今天浏览 何登成的技术博客 无意中发现了写的blog,二分查找(Binary Search)需要注意的问题,以及在数据库内核中的实现。
随想总结下二分查找的常见问题。
问题背景
今年的实习生招聘考试,我出了一道二分查找(Binary Search)的题目。题目大意如下:
给定一个升序排列的自然数数组,数组中包含重复数字,例如:[1,2,2,3,4,4,4,5,6,7,7]。
问题:给定任意自然数,对数组进行二分查找,返回数组正确的位置,给出函数实现。
注:连续相同的数字,返回第一个匹配位置还是最后一个匹配位置,由函数传入参数决定。
在这片博客中作者也详细说明了,二分查找的重要性,比如在数据库的内核实现中,二分查找是一个非常重要的逻辑,几乎99%以上的
SQL语句(所有索引上的范围扫描/等值查询/Unique查询等),都会使用到二分查找进行数据的定位。 可以看到二分查找在现实的重要性。
二分查找算法的思想
二分查找法主要是解决在“一堆数中找出指定的数”这类问题。
而想要应用二分查找法,这“一堆数”必须有一下特征:
- 存储在数组中
- 有序排列
其实二分查找算法的思想很简单,在《编程珠玑》一书中的描述:
在一个包含x的数组内,二分查找通过对范围的跟综来解决问题。开始时,范围就是整个数组。通过将范围中间的元素
与x比较并丢弃一半范围,范围就被缩小。这个过程一直持续,直到在x被发现,或者那个能够包含t的范围已成为空。
Donald Knuth在他的《Sorting and Searching》一书中指出,尽管第一个二分查找算法早在1946年就被发表,但第一个
没有bug的二分查找算法却是在12年后才被发表出来。
注意中间值下标的计算,如果写成(low+high)/2,low+high可能会溢出,从而导致数组访问出错。改进的方法是将计算方式
写成如下形式:low+ ( (high-low) >>1)。
常见问题解决
在何登成的技术博客中的问题四 “如何查找第一个/最后一个等值”,这个大牛只是简单的说明了下,并没有详细说明怎么解决
这个问题,下面来探讨 怎么解决 当所给有序重复数组 中查找 某个值出现的 第一个 和最后一个位置。
主要是下面三个问题:
1)二分查找元素x的下标,如无 return -1
2)二分查找返回x(可能有重复)第一次出现的下标,如无return -1
3)二分查找返回x(可能有重复)最后一次出现的下标,如无return -1
对于问题1 我们只需要 利用最原始的的二分查找即可。
代码如下:
/*
bin_search 二分查找元素x的下标,如无 return -1
low,high 分别为待查元素的区间的 上下界(包含边界).
x为待查元素.
注意 low <= high
*/
int bin_search(int *a, int low, int high, int x)
{
if(NULL == a || low > high || low <0)
return -1;
int mid;
while(low<=high)//注意是<=,若是<会找不到边界值情况
{
mid = low + ((high-low)>>1);
if(xa[mid])
low = mid +1;
else
return mid;
}
return -1;
} 对于问题2,二分查找返回x(可能有重复 )第一次出现的下标,如无return -1。
我们只需找到x重复出现情况下的第一次出现的下标。则我们只需用a[mid]和元素x进行比较,当a[mid]
此时待查元素肯定在待查区间的右半部分 显然此时 不包括 mid 所以有 low = mid+1, 若a[mid]>=x时, 因为我
们查找的是x第一次出现的位置,我们不关心x最后出现的位置,所以此时high下标为mid,直到 low == high 终止
循环,并且比较a[low]是否为x,若是则 找到。
总的思路是:
把有序序列分成2个序列:[first,mid][mid+1,last) 当 a[mid]
当 a[mid]>=x 时 使用序列[first,mid]。
还是看代码吧。
/*
binS_first二分查找返回x(可能有重复)第一次出现的下标,如无return -1
low,high 分别为待查元素的区间的 上下界(包含边界).
//分成2个序列:[first,mid][mid+1,last)
x为待查元素.注意 循环结束条件,low == high */
int binS_first(int *a, int low, int high, int x)
{
if(NULL == a || low > high || low <0) return -1;
int mid;
while(low>1);//计算中点
if(a[mid]=x
high=mid;
}
if(a[low] == x)
return low;
return -1;
} 对于问题3,二分查找返回x(可能有重复)最后一次出现的下标,如无return -1
其实和问题2的思路差不多。
只是在 while中我们假定 low+1 < high,否则在只有两个或者一个元素时 我们只需在while循环之外判断即可。
接下来的while 情况和问题2等价。我们现在关心的是 x(可能有重复)最后一次出现的下标,所以现在我们不关心他
第一次出现下标的位置, 当 a[mid]<=x 时 low = mid, 否则 a[mid] >x 此时 high = mid -1. 代码如下:
/*
binS_last二分查找返回x(可能有重复)最后一次出现的下标,如无return -1
low,high 分别为待查元素的区间的 上下界(包含边界).
x为待查元素.
注意 循环结束条件,low+1 == high
*/
int binS_last(int *a, int low, int high, int x)
{
if(NULL == a || low > high || low < 0 )
return -1;
int mid;
while(low+1>1);
if(a[mid]<=x) // <=x
low = mid;
else // >x
high=mid-1;
}
if(a[high] == x)//先判断high
return high;
else if(a[low] == x)
return low;
return -1;
} 查找重复元素出现的第一次 最后一次位置总结如下:
二分查找返回x(可能有重复)第一次(最后一次)出现的下标找最小的等号放>=x位置(high),找最大的等号放<=x的位置(low)。
其中a[mid]在和待查找元素x比较中带 = 的,在对low 或者high赋值时一定为 mid,其它情况(<或>)则为mid+(-)1.
总的测试程序。
#include
/*
bin_search 二分查找元素x的下标,如无 return -1
low,high 分别为待查元素的区间的 上下界(包含边界).
x为待查元素.
注意 low <= high
*/
int bin_search(int *a, int low, int high, int x)
{
if(NULL == a || low > high || low < 0 )
return -1;
int mid;
while(low<=high)//注意是<=,若是<会找不到边界值情况
{
mid = low + ((high-low)>>1);
if(xa[mid])
low = mid +1;
else
return mid;
}
return -1;
}
/*
binS_first二分查找返回x(可能有重复)第一次出现的下标,如无return -1
low,high 分别为待查元素的区间的 上下界(包含边界).
//分成2个序列:[first,mid][mid+1,last)
x为待查元素.
注意 循环结束条件,low == high */
int binS_first(int *a, int low, int high, int x)
{
if(NULL == a || low > high || low < 0 )return -1;
int mid;
while(low>1);
if(a[mid]=x
high=mid;
}
if(a[low] == x)
return low;
return -1;
}
/*
binS_last二分查找返回x(可能有重复)最后一次出现的下标,
如无return -1
low,high 分别为待查元素的区间的 上下界(包含边界).
x为待查元素.注意 循环结束条件,low+1 == high */
int binS_last(int *a, int low, int high, int x)
{
if(NULL == a || low > high || low < 0)
return -1;
int mid;
while(low+1>1);
if(a[mid]<=x) // <=x
low = mid;
else // >x
high=mid-1;
}
if(a[high] == x)//先判断high
return high;
else if(a[low] ==x)return low;
return -1;
}
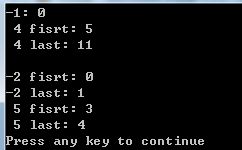
int main()
{
int a[]= {-1,1,2,2,2,4,4,4,4,4,4,4}; //0-11
printf("-1: %d\n", bin_search(a, 0, 11, -1));
printf(" 4 fisrt: %d\n", binS_first(a, 0, 11, 4));
printf(" 4 last: %d\n", binS_last(a, 0, 11, 4));
printf("\n");
int b[]= {-2,-2,0,5,5,7,7}; //0-6
printf("-2 fisrt: %d\n", binS_first(b, 0, 6, -2));
printf("-2 last: %d\n", binS_last(b, 0, 6, -2));
printf(" 5 fisrt: %d\n", binS_first(b, 0, 6, 5));
printf(" 5 last: %d\n", binS_last(b, 0, 6, 5));
return 0;
}
此外对于像,二分查找返回刚好小于x的元素下标,二分查找返回刚好大于x的元素下标, 返回有序数列某一个元素重复出现的次数等问题,可以根据上面
的寻找重复元素出现第一次 最后一次位置的方法 进行 问题求解。对于这类问题也可以参考 STL 中关于 lower_bound与upper_bound的实现。STL算法库
中已经有相关实现。
参考:
http://hedengcheng.com/?p=595
编程珠玑