【有限元分析】有限元仿真分析与解析解的结果对比——以阶梯轴的静力分析为例

（1）对一个阶梯轴零件进行基于材料力学的理论计算，求解最大应力值；
（2）在WORKBENCH中对该阶梯轴零件进行有限元仿真，实行两种仿真方案，分别是1.梁模型建模+梁单元网格划分；2.实体模型建模+六面体单元网格划分，观察两种仿真结果并与理论计算结果的对比，对比结果发现解析解与仿真解相差很小。
（3）可以借此算例学习WB中的梁单元静力分析、三维实体静力分析、理解并施加若干种边界条件，举一反三即可了解此类轴系中轴零件的强度分析。

在进行阶梯轴零件设计的时候一般会对其进行强度校核，校核方式主要有理论计算和仿真分析两种。轴零件的强度校核计算方式已经标准化，查阅手册即可，仿真分析可使用有限元仿真软件，本文算例将在ANSYS WORKBENCH 进行。

本文的算例来自于《ANSYS Workbench 工程实例详解》，以校核阶梯轴强度问题为例，探讨使用解析解解法和有限元分析解的差异。

一、算例描述及其解析解
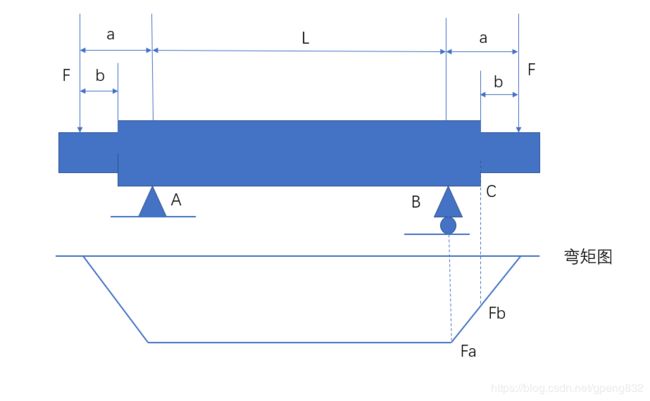
图1为阶梯轴的简图，现校核其受载后的静强度，已知直径$d_1=180mm$，$d_2=150mm$，$a=300mm$，$b=200mm$，$L=1000mm$，$F=300kN$，材料为45，弹性模量$E=2.1e11Pa$，泊松比$v=0.28$，屈服应力${\delta }_s=355MPa$。在AB段，轴只受弯矩$M_{AB}$，而外伸到加载处的这一段，既受弯矩又有剪力，属于横力弯曲。根据材料力学分析，最大正应力应该产生在C截面的圆边缘处，强度为：
${\delta }_{max}={\delta }_c=M_C/W_C=32Fb/\pi {d_2}^3=181.083MPa$
同理AB段的最大应力大小为：${\delta }_{AB}=M_{AB}/W_{AB}=32Fa/\pi {d_1}^3=157.19MPa$

图1 算例的理论解法

二、有限元仿真分析结果
为了简化仿真分析难度，考虑到目前ANSYS Workbench已经普及，且其流程化的操作方式也被越来越多的机械工程师所接受，故本文使用该仿真平台。

在有限元分析的操作过程中，流程可简化为**建模→网格划分→设置边界条件→求解→结果后处理。**就重要性来说，前处理过程包括建模，网格划分和设置边界条件都是非常关键的步骤。网格划分需要考虑网格的类型、形状和尺寸等因素，而在设置边界条件时需确保对模型施加的边界条件与实际加载工况一致，三者均需保证准确无误，否则会导致计算结果与实际情况大相径庭，误导未来的进一步设计。

梁单元静力学分析：
当结构长度对横截面的比率超过10:1，沿长度方向的应力为主要分析对象，且横截面始终保持不变时，在WB中默认为铁摩辛柯梁单元，即beam188和beam189，可计算弯曲、轴向、扭转、和横向剪切变形。beam188和beam189两者的区别是形函数种类不同。beam189的精度更高，计算消耗内存也多，所以在仿真时需要权衡计算精度和时间。本文均使用beam188。

建模：
很多人在最初学习WB的时候，已经掌握了一种或多种三维绘图软件（例如SW、PRO/E等），并且认为只需使用这些三维软件绘制三维图再转化相应格式并将其导入WB中即可。但是这种导入的模型，在进行前处理划分网格的时候只能使用三维实体单元划分网格，而不能使用梁单元、二维平面单元和三维壳单元。例如本文中的算例，若要使用梁单元划分网格，必须在WB中DM模块中建立line body模型，具体参见《ANSYS Workbench 工程实例详解》。

划分网格：
使用line body生成的模型，可以选择自动划分网格的，WB会将以梁单元将其划分完成，例如图2所示。

图2梁模型建模后划分的网格

使用DM建立的solid模型或者通过其它三维软件绘制并导入的模型，可以划分为六面体网格。例如图3所示。

图3 三维实体建模后划分的网格

设置边界条件：
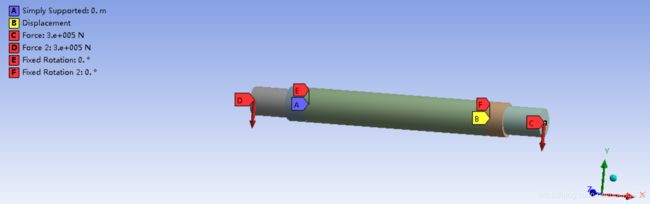
梁模型设置边界条件：需考虑零件的受载和约束，受载即为该轴在两端外侧分别受到大小为300kN的力，方向沿-Y方向。约束需考虑图1中所示的A和B两点：A点是简支约束，在受载后只会产生绕Z轴的旋转，其它自由度均被锁死，故需要在A点施加约束Simply Support和Fixed Rotation（X和Y设置成Fixed，Z设置成Free）；B点有X方向上有平移自由度，和绕Z轴的转动，故需在B点施加约束Fixed rotation（X和Y设置成Fixed，Z设置成Free）和Displacement（X方向设置为free，Y和Z设置为0）。如图4所示。注意下图中的字母标识为软件自动生成，与上述算例描述无关。

图4 梁模型施加边界条件

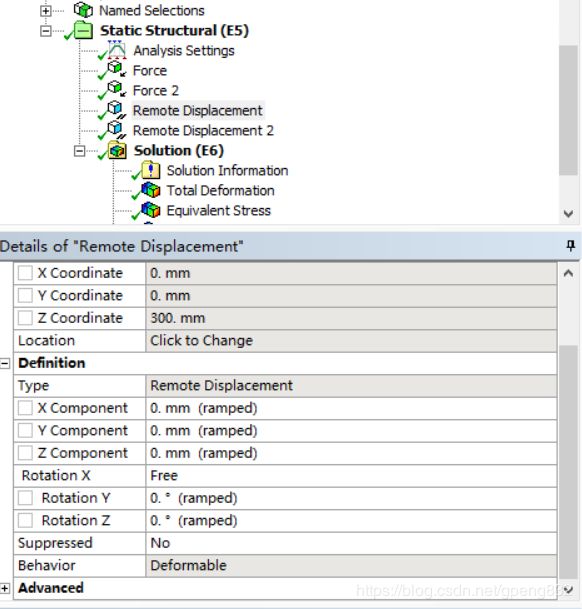
三维实体模型设置边界条件：可在两端面加载大小为300kN的力，设置约束时可使用远程边界条件-远程位移，来设置A和B两点的自由度，在添加远程边界条件时可基于remote point。如图5-图7所示，添加基于A和B所在面与轴相交的外圆线生成的remote point。（关于远程边界条件和远程点，感兴趣的同学可以参看ANSYS Workbench Help 文件）

图5 三维实体模型施加的边界条件

图6 A点remote point的设置

图7 B点remote point的设置

结果和后处理：
梁模型的后处理需导入 Beam Tool→Maximum Combined Stress，求解零件的在各个位置的最大应力，结果如下所示，如预期所料最大应力值出现在C截面，最大值如左侧的颜色条所示：

图8 梁模型应力分布

结论：最大应力值为181.46MPa，理论值为181.08MPa，误差为0.1%。

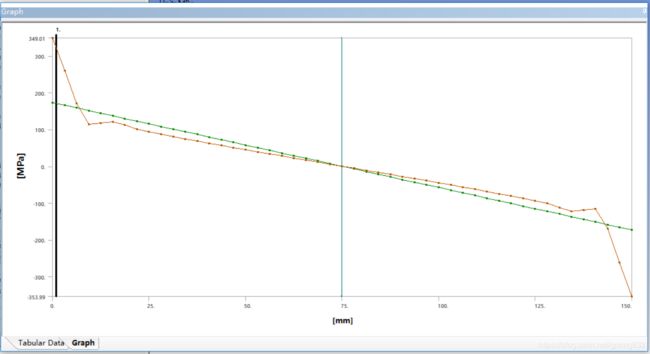
三维实体模型的von-mises应力云图如图9所示，但是求解的最大的应力值为258.44MPa，与理论计算值不符，这是因为由于有限元计算的特点，在该处会出现应力集中的现象。所以再分析C截面的应力值。

图9 实体模型应力云图

图10 C截面上的路径

图11 应力值随路径位置的变化

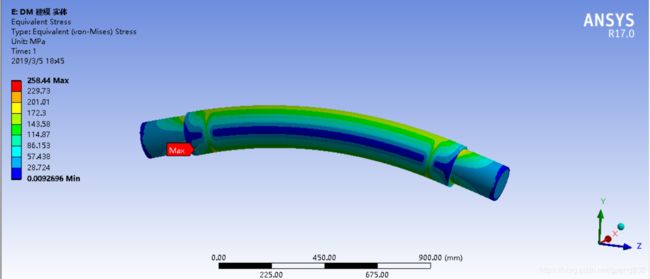
由于应力集中导致峰值应力相差很大，所以反映的总应力相差也很大。

结论：C截面的弯曲应力为173.15MPa，理论值为181MPa，误差小于5%。