数据挖掘第一课学习笔记(Apriori算法和FPTree算法)
首先明确关联规则挖掘中的几个概念定义:
假设有数据集表示几个客户买的东西如下:
t1: 牛肉、鸡肉、牛奶
t2: 牛肉、奶酪
t3: 奶酪、靴子
t4: 牛肉、鸡肉、奶酪
t5: 牛肉、鸡肉、衣服、奶酪、牛奶
t6: 鸡肉、衣服、牛奶
t7: 鸡肉、牛奶、衣服ti表示不同的客户在一次购物中买的东西,那么:
事务&事务集合:每次顾客购买的一次商品集合ti就称作一个事务,所有的T={t1,t2……t7}称作事务集合。
商品集合:这个很好理解,就是所有商品的集合I={牛肉、鸡肉、牛奶、奶酪、靴子、衣服}
支持度&置信度:对于一条规则X—>Y,它的支持度(support)=(X,Y).count/T.count(x,y同时出现的事务数除以总事务数),置信度(confidence)=(X,Y).count/X.count (x,y同时出现的事务数除以x出现的事务数)。其中(X,Y).count表示T中同时包含X和Y的事务的个数,X.count表示T中包含X的事务的个数。
举例来说,假如有一条规则为牛肉—>鸡肉,那么同时购买牛肉和鸡肉的顾客比例是3/7,而购买牛肉的顾客当中也购买了鸡肉的顾客比例是3/4。这两个比例参数是很重要的衡量指标,它们在关联规则中称作支持度(support)和置信度(confidence)。对于规则:牛肉—>鸡肉,它的支持度为3/7,表示在所有顾客当中有3/7同时购买牛肉和鸡肉,其反应了同时购买牛肉和鸡肉的顾客在所有顾客当中的覆盖范围;它的置信度为3/4,表示在买了牛肉的顾客当中有3/4的人买了鸡肉,其反应了可预测的程度,即顾客买了牛肉的话有多大可能性买鸡肉。
频繁项集:这个就用百度百科的做解释吧,项的集合称为项集。包含k个项的项集称为k-项集。例如集合{computer,ativirus_software}是一个二项集。项集的出项频率是包含项集的事务数,简称为项集的频率,如果项集I的相对支持度满足预定义的最小支持度阈值,则I是频繁项集。
Apriori算法
第k级会生成 k项集 和 过滤掉非频繁项集,保留下k项频繁项集。
每一级的构建都会引起数据量的增加,而每一级的过滤后,会大大减少数据量,便于下一级的运算。
逐步过滤和合并,直至生成极少数量的频繁项集,或者极大频繁项集.
Aprior有点类似广度优先的算法。
1,2,3
1,2,4
1,3,4
1,2,3,5
1,3,5
2,4,5
1,2,3,4{1,2},{1,3},{1,4},{1,5}
{2,3},{2,4},{2,5}
{3,4},{3,5}
{4,5}
相对来讲,还是比较好理解的。
FP-tree算法
牛奶,鸡蛋,面包,薯片
鸡蛋,爆米花,薯片,啤酒
鸡蛋,面包,薯片
牛奶,鸡蛋,面包,爆米花,薯片,啤酒
牛奶,面包,啤酒
鸡蛋,面包,啤酒
牛奶,面包,薯片
牛奶,鸡蛋,面包,黄油,薯片
牛奶,鸡蛋,黄油,薯片第一次扫描完毕得到的1-项频繁集(已经完成过滤的):
薯片,鸡蛋,面包,牛奶
薯片,鸡蛋,啤酒
薯片,鸡蛋,面包
薯片,鸡蛋,面包,牛奶,啤酒
面包,牛奶,啤酒
鸡蛋,面包,啤酒
薯片,面包,牛奶
薯片,鸡蛋,面包,牛奶
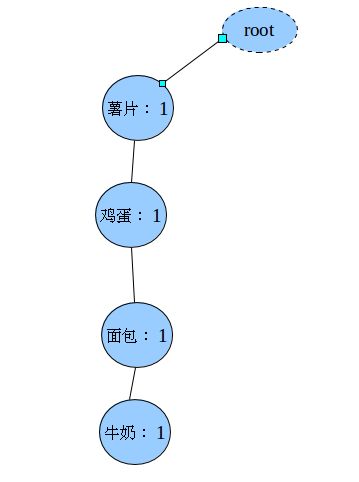
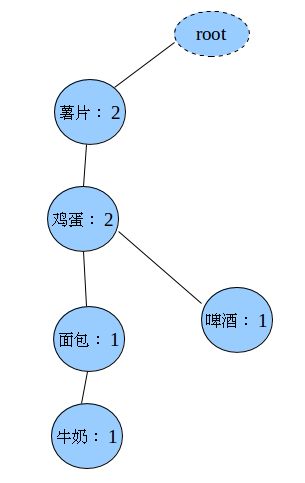
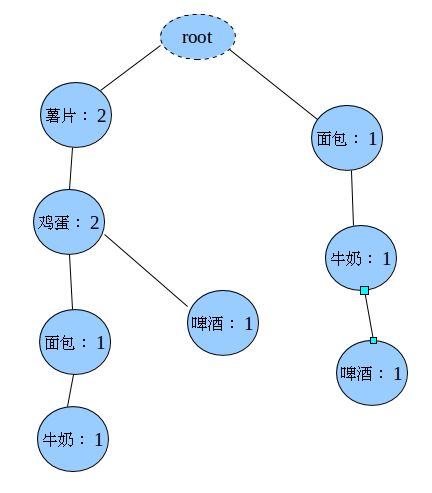
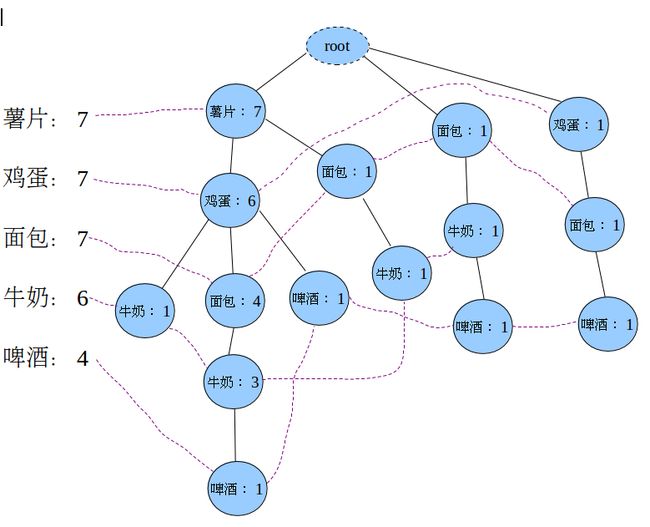
薯片,鸡蛋,牛奶第三步:构造FP-Tree
上面的虚线表示的是指针的链表,表头项的每一项都指向了自己出现的每个每个节点连成一条线(比如表头项薯片指向的就是所有薯片节点,连成一条线)。
第三步:调用算法:
3、 调用FP-growth(Tree,null)开始进行挖掘。伪代码如下,其中Tree为树,a是后缀。初始为初始FP-tree,后缀为空:
procedure FP_growth(Tree, a)
if Tree 是单条路径P then{
for 路径P中结点的每个组合(记作b)
产生模式b U a,其支持度support = b 中结点的最小支持度;
} else {
for each a i 在Tree的表头项(head)里面的{
产生一个模式b = a i U a,其支持度support = a i .support;
构造b的条件模式基,然后构造b的条件FP-树Treeb;
if Treeb 不为空 then
调用 FP_growth (Treeb, b);
}
}
构造条件模式基意思是:包含FP-Tree中与后缀模式一起出现的前缀路径的集合。也就是同一个频繁项在PF树中的所有节点的祖先路径的集合。
然后把这个集合,再作为事务数据库进行一个构造FP-Tree的操作就得到了条件FP-Tree(只是这个时候传入进来的后缀不为NULL了)。
http://blog.csdn.net/sealyao/article/details/6460578/
http://blog.csdn.net/huagong_adu/article/details/17739247
这两篇博客我觉得讲的比较好,不太理解的地方还可以看下。