数据结构算法代码实现——线性表的顺序表示与实现(二)
线性表的顺序表示
线性表的顺序表示:指的是一组地址连续的存储单元依次存储线性表的数据元素。
顺序表的存储方法与特点
在日常生活中,我们通常更喜欢使用连续的存储空间来存放各种物品。
好,举个例子:假设宿舍内的床铺用编号1-6,宿舍内成员按年龄分出老大-老六,老大使用编号为1的床铺。依次类推。
这种安排方式可以使我们通过床铺编号快速找到同学。
顺序表的存储方式也与此类似,下面讨论顺序表的特点:
1. 顺序存储结构的逻辑存储和存储结构一致
2. 访问每个数据元素所花费的时间相同,利用数学公式
3. 存取元素的方法称为随机存取法,也称为随机存储结构。
顺序存储结构表示
//----线性表的动态分配顺序存储结构----
#define LIST_INIT_SIZE 10 //线性表存储空间的初始分配量
#define LISTADD 5 //线性表存储空间的分配增量
typedef struct {
ElemType * elem; //存储空间基址(数组的基地址)
int length;//当前长度
int listsize;//当前分配的存储总容量(sizeof(ElemType)为单位)
}Sqlist;见严蔚敏教材22页。
顺序表的基本操作(C语言)
基本操作包括了教材19页的12个操作,其中的操作也实现了教材中的2.3,2.4,2.5,2.6算法。
C语言代码:
1,先给出头文件:
#include
#include
#include
// 函数结果状态代码
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define OVERFLOW -1
typedef int Status; //Status是函数的类型,其值是函数结果状态代码,如OK等
typedef int Boolean; // Boolean是布尔类型2,在给出基本操作代码:
//----线性表的动态分配顺序存储结构----
#define LIST_INIT_SIZE 10 //线性表存储空间的初始分配量
#define LISTADD 5 //线性表存储空间的分配增量
typedef struct {
ElemType * elem; //存储空间基址(数组的基地址)
int length;//当前长度
int listsize;//当前分配的存储总容量(sizeof(ElemType)为单位)
}Sqlist;
//----顺序表示的线性表的基本操作(12个包括了书中有关操作的算法)
// 1, InitList(&L) 操作结果:构造一个空的顺序表L。书中算法2.3
Status InitList(Sqlist *L){
(*L).elem=(ElemType *)malloc(LIST_INIT_SIZE*sizeof(ElemType));
if(!(*L).elem) exit(OVERFLOW);//exit(-1) 存储空间失败
(*L).length=0; //初始化空表长度为0
(*L).listsize=LIST_INIT_SIZE; //初始化空表的存储总容量
return OK; //返回状态码 1
}
// 2, DestroyList(&L) 初始条件:顺序表L已存在。 操作结果:销毁顺序表L。
Status DestroyList(Sqlist *L){
free((*L).elem);
(*L).elem=NULL; //指向空
(*L).length=0;
(*L).listsize=0;
return OK;
}
//3, ClearList(&L) 初始条件:顺序表L已经存在。操作结果:将L重置为空表。
Status ClearList(Sqlist *L){
(*L).length=0; //清空当前长度
return OK;
}
//4, ListEmpty(L) 初始条件:顺序表L已存在。操作结果:若顺序表L为空返回TRUE,否则返回FLASE。
Status ListEmpty(Sqlist L){
if(L.length==0)
return TRUE;
else
return FALSE;
}
//5, ListLength(L) 初始条件:顺序表L已存在。操作结果:返回L中数据元素的个数。
int ListLength(Sqlist L){
return L.length;
}
//6, GetElem(L,i,&e) 初始条件:顺序表L已存在(1<=i<=ListLength(L))。操作结果:用e返回L中i个数据元素的值。
Status GetElem(Sqlist L,int i,ElemType *e){
if(i<1||i>L.length)
exit(ERROR);
*e=L.elem[i-1];//*e=*(L.elem+i-1)
return OK;
}
//7, LocateElem(L,e,compare()) 初始条件:顺序表L已存在,compare()的数据元素判定函数。
// 操作结果:返回L中第1个与e的满足关系compare()的数据元素的位序。若这样的数据元素不存在,则返回0.
// 书中算法2.6(进行两个元素之间的比较) 时间复杂度为O(L.length)
int LocateElem(Sqlist L,ElemType e,Status (*compare)(ElemType,ElemType)){//compare()形参是函数指针
/*
*/
int i =1; //i的初值为第一个元素的位序
ElemType *p=L.elem; //p的初值为第一个元素的存储位置
while(i<=L.length && !(*compare)((*p++),e)){
++i;
}
if(i<=L.length) return i;
else
return 0;
}
//8, PriorElem(L,cur_e,&pre_e) 初始条件:顺序表L已存在。
//操作结果:若cur_e是L的数据元素,且不是第一个,则用pre_e返回它的前驱,否则操作失败,pre_e无定义。
Status PriorElem(Sqlist L,ElemType cur_e,ElemType *pre_e){
ElemType *p =L.elem+1; //指针变量p 指向第二个数据元素
int i =2;
while(i<=L.length && (*p)!=cur_e){ //注意不能写成,(*p++)!=cur_e,虽然它先判断*p,在+1,
//但是在条件不成立时会多后移一个位置
p++;
++i;
}
if(i>L.length){
return ERROR;
}else{
*pre_e=(*--p); //p先自减,pre_e就指向该数据元素的前驱结点
return OK;
}
}
//9, NextElem(L,cur_e,&next_e) 初始条件:顺序表L已存在。
//操作结果:若cur_e是L的数据元素,且不是第一个,则用next_e返回它的前驱,否则操作失败,next_e无定义。
Status NextElem(Sqlist L,ElemType cur_e,ElemType *next_e){
ElemType *p =L.elem;
int i=1;
while(i
=L.length){
return ERROR;
}else{
*next_e =(*++p); //next_e指向该数据元素的后继结点
return OK;
}
}
//10, ListInsert(Sqlist *L,i,e) 初始条件:顺序表L已存在,1<=i<=ListLength(L)+1。
//操作结果:在L中第i个位置之前插入新的数据元素e,L的长度加1
/*
书中算法2.4
算法语言描述:
1,检查插入位置i的有效性,插入位置i的有效范围是1<=i<=ListLength(L)+1(注意:顺序表尾也能执行插入操作)。
2,在插入之前先检查顺序表是否已满(判断顺序表的length是否等于listsize),在顺序表满的时候不能进行插入运算,需要申请内存空间。
3,后移i位置以后的数据元素,为新数据元素让去第i个位置。
4,将新元素e插入第i个位置。
5,将当前的顺序表length加1.
*/
Status ListInsert(Sqlist *L,int i,ElemType e){
ElemType *q,*p,*newbase=NULL;
//第一步
if(i<1 || i>(*L).length+1){ //i的值不合法
return ERROR;
}
//第二步
if( (*L).length >=(*L).listsize){ /* 当前存储空间已满,增加分配 */
newbase =(ElemType *)realloc((*L).elem , ((*L).listsize+LISTADD)*sizeof(ElemType));
if(!newbase) exit(OVERFLOW);
(*L).elem =newbase; //新基址
(*L).listsize +=LISTADD; //增加存储容量
}
//第三步
q =&((*L).elem[i-1]); //q为插入位置(或q =(*L).elem+i-1。)
for(p =&((*L).elem[(*L).length-1]);p >=q;--p){ //或p =((*L).elem+(*L).length-1)
*(p+1) =*p;
}
/*或
int j;
for(j =(*L).length;j >=i;--j){
(*L).elem[j] =(*L).elem[j-1]; //或 *((*L).elem+j) =((*L).elem+j-1)
}
(*L).elem[j-1]=e;*/
//第四步
*q =e; //插入数据元素
//第五步
++(*L).length;
return OK;
}
//11, ListDelete(Sqlist &L,int i,ElemType &e) 初始条件:顺序线性表L已存在,1<=i<=ListLength(L)
// 操作结果:删除L的第i个数据元素,并用e返回其值,L的长度减1
/*
书中算法2.5
算法语言描述:
1,检查插入位置i的有效性,删除位置i的有效范围是1<=i<=ListLength(L)。
2,在插入之前先检查顺序表是否为空(length!=0)。
3,前移i+1位置以后的数据元素(注意:从i+1的位置开始,要覆盖第i个位置)。
4,将当前的顺序表length减1.
*/
Status ListDelete(Sqlist *L,int i,ElemType *e){
ElemType *q,*p=NULL;
//第一步,第二步
if(i <1 || i>(*L).length) return ERROR; //注意此处包含了第二步的检查
//第三步
p =&((*L).elem[i-1]); //p为被删除元素的位置
*e =*p;
q =(*L).elem+(*L).length-1;
for(++p;p <=q;++p){ //
*(p-1) =(*p);
}
/*或
p =&((*L).elem[i-1]); //p为被删除元素的位置
*e =*p;
for(q =&((*L).elem[(*L).length-1]);p
<=j;++i){ //i在数组中的下标映射是被删除位置的后一个数据元素
(*L).elem[i-1]=(*L).elem[i];//或*((*L).elem+i-1)=*((*L).elem+i)
}*/
//第四步
--(*L).length;
return OK;
}
//12, ListTraverse(L,visit())
/* 初始条件:顺序线性表L已存在。
操作结果:依次对L的每个数据元素调用函数visit()。一旦visit()失败,则操作失败 */
Status ListTraverse(Sqlist L,void (*visit)(ElemType*)){ //visit()的形参加&,意味着visit()可以修改L.elem中数据元素的值
int i=1;
ElemType *p=L.elem;
for(i=1;i<=L.length;i++)
(*visit)(p++);
printf("\n");
return OK;
}
3,然后给出测试上述操作的C代码:
测试:
#include"ch2.h"
typedef int ElemType;
#include"sequence_list.c"
Status equal(ElemType c1,ElemType c2)
{
if(c1==c2)
return TRUE;
else
return FALSE;
}
void visit(ElemType *c)
{
printf("%d ",*c);
}
void main()
{
Sqlist L;
Status i;
int j,j1;
ElemType e,e1;
//1, 测试第一个基本操作(构造顺序表L)
printf("1,测试第一个基本操作(构造顺序表L)\n");
i=InitList(&L);
printf(" 初始化顺序表L后:L.elem=%d L.length=%d L.listsize=%d\n",L.elem,L.length,L.listsize);
printf("\n");
//2, 测试第十个基本操作(插入数据元素)
printf("2,测试第十个基本操作(插入数据元素)\n");
for(j=1;j<=5;j++){
ListInsert(&L,1,j);
}
printf(" 在L的表头插入1-5数据后:L.elem=%d(没有改变) L.length=%d L.listsize=%d\n",L.elem,L.length,L.listsize);
printf(" 在L的表头依次插入1~5后:*L.elem=");
for(j=1;j<=5;j++){
printf("%d ",L.elem[j-1]); //或 *(L.elem+j-1)
}
printf("\n");
//测试存储空间已满,增加分配
for(j=6;j<=11;j++){
ListInsert(&L,j,j);
}
printf(" 在L表头插入1-5数据后,然后在 L表尾 追加6-11:L.elem=%d(有可能不改变) L.length=%d(改变) L.listsize=%d(改变)\n",L.elem,L.length,L.listsize);
printf(" 此时L表中数据元素:*L.elem=");
for(j=1;j<=11;j++){
printf("%d ",L.elem[j-1]); //或 *(L.elem+j-1)
}
printf("\n");
printf("\n");
//3, 测试第三、四个操作
printf("3, 测试第三、四个操作\n");
i=ListEmpty(L);
printf(" L是否空:i=%d(1:是 0:否)\n",i);
i=ClearList(&L);
printf(" 清空L后:L.elem=%u L.length=%d L.listsize=%d\n",L.elem,L.length,L.listsize);
i=ListEmpty(L);
printf(" L是否空:i=%d(1:是 0:否)\n",i);
//再次插入数据1-11
for(j=1;j<=11;j++){//注意如果j=0时,将会在插入操作中触发第一步i值不合法。
ListInsert(&L,j,j);
}
printf(" 有插入了11条数据\n");
ListTraverse(L,visit);
printf("\n");
//4,测试第五个操作
printf("4,测试第五个操作(L的数据元素个数)\n");
printf(" L表的长度=%d\n",L.length);
printf("\n");
//5, 测试第六个操作
printf("5, 测试第六个操作(取得第5个位置的数据元素)\n");
i=GetElem(L,5,&e);
printf(" 第5个位置的数据元素:%d\n",e);
printf("\n");
//6,测试第七个操作
printf("6,测试第七个操作(LocateElem)\n");
j=LocateElem(L,11,equal);
if(i>0)
printf(" 在L表中存在于11相同的元素,位序是:%d\n",j);
else
printf(" 在L表中不存在与11相同的数据元素\n");
printf("\n");
//7,测试第八、九个操作
printf("7,测试第八、九个操作\n");
for(j=1;j<=2;j++){ // 测试头两个数据
GetElem(L,j,&e1); // 把第j个数据赋给e1
i=PriorElem(L,e1,&e); // 求e1数据元素的前驱
if(i==ERROR)
printf(" 元素%d无前驱\n",e1);
else
printf(" 元素< %d的前驱为:%d >\n",e1,e);
}
for(j=ListLength(L)-1;j<=ListLength(L);j++){ // 最后两个数据
GetElem(L,j,&e1); // 把第j个数据赋给e1
i=NextElem(L,e1,&e); // 求e1的后继
if(i==ERROR)
printf(" 元素%d无后继\n",e1);
else
printf(" 元素< %d的后继为:%d >\n",e1,e);
}
printf("\n");
//8,测试第十个操作(删除操作)
printf("8,测试第十一个操作(删除操作)\n");
j1=ListLength(L); //注意要把表L的长度先保存到一个变量中,因为在删除时,表的长度会自减一的。
for(j=j1+1;j>=j1;j--){
i=ListDelete(&L,j,&e); // 删除第j个数据
if(i==ERROR)
printf(" 删除第%d个数据失败\n",j);
else
printf(" 删除的元素值为:%d\n",e);
}
printf("\n");
//9,测试第十二个操作
printf("9,测试第十二个操作\n");
ListTraverse(L,visit);
printf("\n");
//10,测试第二个操作
printf("10,测试第二个操作\n");
DestroyList(&L);
printf(" 销毁L后:L.elem=%u L.length=%d L.listsize=%d\n",L.elem,L.length,L.listsize);
}
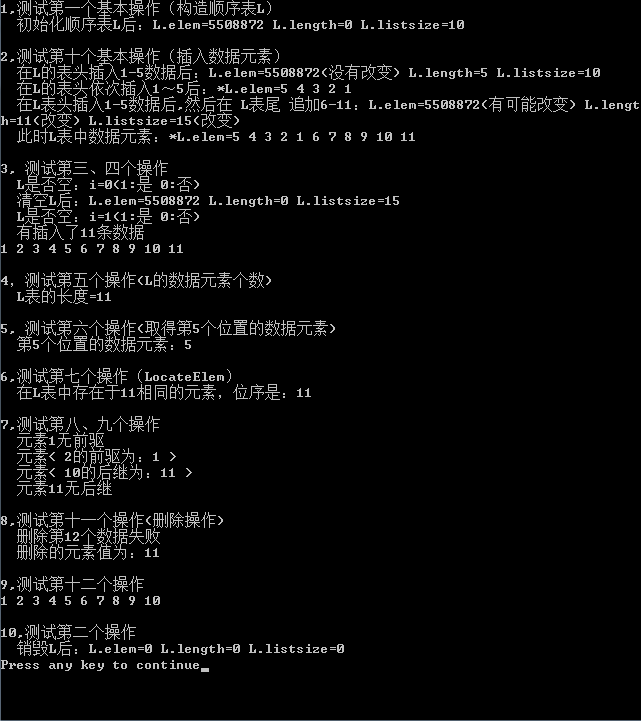
4,最后在给出测试结果图:
5,总结
上述操作中需要重点掌握的算法是,初始化、插入、删除等等。比较重点的基本操作在代码中都有自然语言算法描述和注释。
如需详细了解,请见教材。
下面,我们简单了解一下比较重要操作的问题:
1,书中算法2.4是插入操作:
假定插入线性表中任一元素的概率相同(都为1/n+1),则插入一个元素平均需要移动元素的个数是n/2。
个数取决于插入的位置,假定在顺序表任何插入位置的概率是相等的,则平均情况下,需要移动一半的数据元素。
2,书中算法2.5是删除操作:
假定删除线性表中任一元素的概率相同(都为1/n),则删除一个元素平均需要移动元素的个数是(n-1)/2。
删除的时间复杂度也是O(n)。
3,书中算法2.6是根据满足关系执行操作
基本操作是“进行两个元素之间的比较”,需要遍历表中的数据元素与e比较。可见时间复杂度与表的长度有关,
所以时间复杂度为O(L.length)。
较复杂的操作算法实现
上述的算法是一些基本的操作,教材中的2.1,2.2,2.7算法是较复杂的算法(多种基本操作的组合使用)。
合并后的表仍然是非递减有序排列。
1. 算法2.1
C语言算法实现:
#include"ch2.h"
typedef int ElemType;
#include"sequence_list.c"
Status equal(ElemType a,ElemType b){
if(a == b){
return TRUE;
}else{
return FALSE;
}
}
/*
自然语言描述算法:
1,求的顺序表的长度
2,依次访问Lb中的数据元素
若取得数据元素与La中的不相同,则插入之。
*/
void Union(Sqlist *La,Sqlist Lb){
ElemType e;
int la_len,lb_len;
int i;
//第一步
la_len =ListLength(*La);
lb_len =ListLength(Lb);
//第二步
for(i=1;i<=lb_len;++i){
GetElem(Lb,i,&e);//依次取得Lb的数据元素
if(!LocateElem( *La,e,equal)){//不相同则插入之
ListInsert( La,++la_len,e);
}
}
}
void print(ElemType *c)
{
printf("%d ",*c);
}
void main(){
Sqlist La , Lb;
Status i;
int j;
//初始化顺序表La和Lb
printf("1,初始化顺序表La和Lb\n");
i =InitList(&La); //构造空的顺序表
if(i==1){ //成功
for(j=1;j <=3;j++){ //注意如果j=0时,将会在插入操作中触发第一步i值不合法。
ListInsert(&La,j,j); //插入操作
}
}
printf("初始化成功表La的数据元素:");
ListTraverse(La,print);
InitList(&Lb);
for(j=1;j<=11;j++){
ListInsert(&Lb,j,j);
}
printf("初始化成功表La的数据元素:");
ListTraverse(Lb,print);
printf("\n");
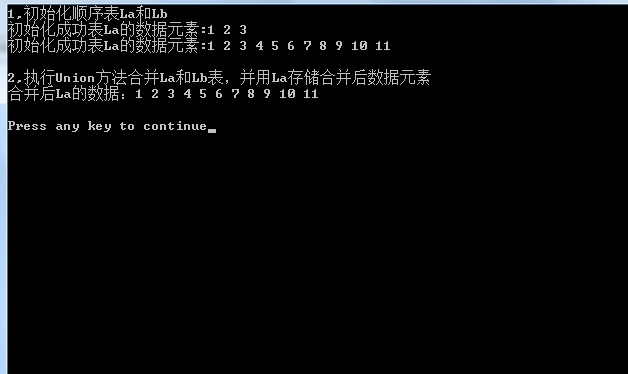
//执行Union方法合并La和Lb表,并用La存储合并后数据元素
printf("2,执行Union方法合并La和Lb表,并用La存储合并后数据元素\n");
Union(&La,Lb);
printf("合并后La的数据:");
ListTraverse(La,print);
printf("\n");
}
2. 算法2.2和算法2.7 和 书中26页对2.7的改进算法 都在下述代码中
需要一个计算时间的文件,用于测试不同算法的时间:
```
#include
void kaishi(DWORD *start){
*start = GetTickCount();
}
void end(DWORD *stop){
*stop = GetTickCount();
}
void time_printf(DWORD start,DWORD stop){
printf("time: %lld ms\n", stop - start);
}
```
C语言算法实现:
#include"ch2.h"
typedef int ElemType;
#include"sequence_list.c"
#include"time_.c"
/*
算法分析:
1,初始化表Lc,并定义3个标志变量i,j,k
2,利用while循环,取得表La和Lb相同位序的数据元素,比较之在插入表Lc中,使之产生前后位序。
3,判断表La和Lb中是否还有剩余的数据元素,在插入表Lc的尾部。
*/
/*
算法2.2
*/
void MergeList(Sqlist La,Sqlist Lb,Sqlist *Lc){
int i=1,j=1,k =0;//记忆 表La、Lb、Lc的当前长度
int la_len,lb_len;
ElemType ai,bj;
//第一步
InitList(Lc);
//第二步
la_len =ListLength(La);
lb_len =ListLength(Lb);
while((i<=la_len) && (j<=lb_len)){
//取得数据元素
GetElem(La,i,&ai);
GetElem(Lb,j,&bj);
//比较
if(ai<=bj){
ListInsert(Lc,++k,ai); //插入之
++i;
}else{
ListInsert(Lc,++k,bj);
++j;
}
}
//第三步
while(i<=la_len){
GetElem(La,i,&ai);
ListInsert(Lc,++k,ai);
i++;
}
while(j<=lb_len){
GetElem(Lb,j,&bj);
ListInsert(Lc,++k,bj);
j++;
}
}
/*
算法2.7利用指针操作数据元素赋值
*/
void MergeList_2(Sqlist La,Sqlist Lb,Sqlist *Lc){
ElemType *a,*b, *a_last,*b_last, *c=NULL;
//初始化表Lc
InitList(Lc);
//利用指针指向La和Lb中elem数据元素的头和尾
a =La.elem;
b =Lb.elem;
a_last =La.elem+ListLength(La)-1;
b_last =Lb.elem+ListLength(Lb)-1;
//重新定义初始化表Lc
(*Lc).length=(*Lc).listsize=ListLength(La)+ListLength(Lb);
(*Lc).elem=(ElemType *)malloc((*Lc).listsize*sizeof(ElemType));
if(!(*Lc).elem) exit(OVERFLOW);
c =(*Lc).elem;
//第二步
while(a<=a_last && b
b)
i=-1;
return i;
}
Status equal(ElemType a,ElemType b){
if(a == b){
return TRUE;
}else{
return FALSE;
}
}
void print(ElemType *c)
{
printf("%d ",*c);
}
/*
对算法2.7的改进
*/
void MergeList_3(Sqlist La,Sqlist Lb,Sqlist *Lc){
ElemType *a,*b, *a_last,*b_last, *c=NULL;
//初始化表Lc
InitList(Lc);
//利用指针指向La和Lb中elem数据元素的头和尾
a =La.elem;
b =Lb.elem;
a_last =La.elem+ListLength(La)-1;
b_last =Lb.elem+ListLength(Lb)-1;
//重新定义初始化表Lc
(*Lc).listsize=ListLength(La)+ListLength(Lb); //注意:不用设置length,假设有重复,则在调用ListTraverse会输出野指针
(*Lc).elem=(ElemType *)malloc((*Lc).listsize*sizeof(ElemType));
if(!(*Lc).elem) exit(OVERFLOW);
c =(*Lc).elem;
//第二步
while(a<=a_last && b
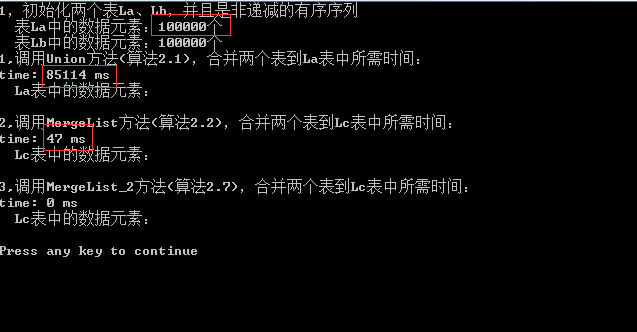
然后看不同算法的时间比较图(含2.1算法union())
对于时间的比较 在最后被注释的代码,可以自行修改代码进行不同算法的时间比较 。下面我们进行两次比较:算法2.1
、算法2.2的比较 和算法2.2与2.7的比较。
3. 总结
对于算法的评论,可以依据时间复杂度,当然这不是评价的唯一标准。
1,首先先看算法2.1:
在此算法中的一些基本操作如GetElem、ListInsert(在表尾插入)的执行时间复杂度和表长无关。LocateElem
的执行时间和表长成正比,所以算法2.1的时间复杂度为O(ListLength(LA) * ListLength(LB))。
2,在看算法2.2:
在此算法的基本操作和算法2.1相同,但是算法时间复杂度却不同,算法2.2的时间复杂度为O(ListLength(LA) + ListLength(LB))。
从上面的时间比较图(1),就可以看出在有100000条数据时,算法2.2相对算法2.1节省了1800倍。
3,最后看算法2.7:
在此算法中的基本操作是“元素赋值”,没有上述的一些基本操作。它的时间复杂度也是O(ListLength(LA) + ListLength(LB))。
但是从上面的时间比较图(2),可以看出算法2.7相对算法2.2节省了230倍的时间。所以当两个算法的时间复杂度相同,但是由于不同的基本操作,
可能会有很多的解决方案,我们要选择最优的解决方案,否则在对于大数据的问题将很难解决。
4,算法2.7的改进是为了达到2.1的效果,具体的分析可见教材。注意的是,算法2.1只是链接两个表并去掉重复元素,想将Lb中元素插入La,
算法2.7的改进需要先对表进行数据元素的排序。由此可见,若以线性表表示集合并进行集合的各种运算,应先对表中元素进行排序。
最后讨论一下顺序存储的缺点
人无完人,金无赤足。在数据结构中也是如此,顺序表既然有特点、有优点,顺序表的缺点:
- 对顺序表做插入、删除时,需要大量的移动数据元素。
- 线性表需要预先分配空间,必须按最大空间分配,存储空间得不到充分利用,造成内存浪费。