目录
- 矩阵乘法
- 1. 算法分析
- 2. 板子
- 3. 例题
- 3.1 直接处理矩阵运算
- 3.2 斐波那契数列+矩阵快速幂
矩阵乘法
1. 算法分析
利用快速幂的方法来优化矩阵的乘法,使得计算矩阵A(N*N)的M次方的时间优化到O(N3logM)
常用技巧
一般如果能够把式子写成 Kn = Kn-1+t,那就能使用矩阵快速幂处理,设Fn=[fn, fn+1, kn], Fn+1=[fn+1, fn+2, kn+1],那么Fn+1=FnA (A为矩阵)
2. 板子
- 计算ax
#include
using namespace std;
typedef long long LL;
const int N = 110, mod = 1e9 + 7;
int n;
// 定义一个矩阵
struct mat
{
int m[N][N];
}unit;
// 定义矩阵乘法
mat operator * (mat a, mat b)
{
mat res;
LL x;
for (int i = 0; i < n; ++i)
for (int j = 0; j < n; ++j)
{
x = 0;
for (int k = 0; k < n; ++k)
x += (LL)a.m[i][k] * b.m[k][j] % mod;
res.m[i][j] = x % mod;
}
return res;
}
// 初始化单位阵
void init_unit()
{
for (int i = 0; i < N; ++i)
unit.m[i][i] = 1;
return ;
}
// 矩阵快速幂
mat pow_mat(mat a, LL n)
{
mat res = unit; // 初始为单位阵
while (n)
{
if (n & 1) res = res * a;
a = a * a;
n >>= 1;
}
return res;
}
int main()
{
LL x;
init_unit();
while (cin >> n >> x)
{
mat a;
for (int i = 0; i < n; ++i)
for (int j = 0; j < n; ++j)
cin >> a.m[i][j];
a = pow_mat(a, x);
for (int i = 0; i < n; ++i)
for (int j = 0; j < n; ++j)
if (j + 1 == n) cout << a.m[i][j] << endl;
else cout << a.m[i][j] << " ";
}
return 0;
}
- 计算斐波那契数列
#include
using namespace std;
typedef long long LL;
const int N = 4, mod = 10000 ;
int n;
// 定义一个矩阵
struct mat
{
int m[N][N];
}unit;
// 定义矩阵乘法
mat operator * (mat a, mat b)
{
mat res;
LL x;
for (int i = 0; i < 2; ++i)
for (int j = 0; j < 2; ++j)
{
x = 0;
for (int k = 0; k < 2; ++k)
x += (LL)a.m[i][k] * b.m[k][j] % mod;
res.m[i][j] = x % mod;
}
return res;
}
// 初始化单位阵
void init_unit()
{
for (int i = 0; i < N; ++i)
unit.m[i][i] = 1;
return ;
}
// 矩阵快速幂
mat pow_mat(mat a, LL n)
{
mat res = unit; // 初始为单位阵
while (n)
{
if (n & 1) res = res * a;
a = a * a;
n >>= 1;
}
return res;
}
int main()
{
init_unit();
while (cin >> n && n != -1)
{
if (!n) {
cout << 0 << endl;
continue;
}
mat a;
a.m[0][0] = 0, a.m[0][1] = 1;
a.m[1][0] = 1, a.m[1][1] = 1;
a = pow_mat(a, n - 1);
LL res = (a.m[1][0] + 0ll + a.m[0][0]) % mod;
cout << res << endl;
}
return 0;
}
3. 例题
3.1 直接处理矩阵运算
acwing225矩阵幂求和
给定n×n矩阵A和正整数k,求和S=A+A2+A3+…+Ak。结果输出时每个元素都需要mod m
1≤n≤30,1≤k≤1e9,1≤m<1e4
/*
分治的思想
Sn = a+a^2+a^3+...a^n
如果n是奇数那么:
Sn = (a + a^2 + ... a^(n/2))*(a^(n/2) + 1) + a^n
如果n是偶数那么:
Sn = (a + a^2 + ... a^(n/2))*(a^(n/2) + 1)
基于这个思想,可以不断把前项进行分治处理
这样时间复杂度为:O(((logk)^2) * n^3 )
*/
#include
using namespace std;
typedef long long LL;
const int N = 31;
int n, k, mod;
// 定义一个矩阵
struct mat
{
int m[N][N];
}unit;
mat a;
// 定义矩阵乘法
mat operator * (mat a, mat b)
{
mat res;
LL x;
for (int i = 0; i < n; ++i)
for (int j = 0; j < n; ++j)
{
x = 0;
for (int k = 0; k < n; ++k)
x += (LL)a.m[i][k] * b.m[k][j] % mod;
res.m[i][j] = x % mod;
}
return res;
}
mat operator + (mat a, mat b) {
mat res;
for (int i = 0 ; i < n; ++i) {
for (int j = 0 ; j < n; ++j) {
res.m[i][j] = ((LL)a.m[i][j] + b.m[i][j]) % mod;
}
}
return res;
}
// 初始化单位阵
void init_unit()
{
for (int i = 0; i < N; ++i)
unit.m[i][i] = 1;
return ;
}
// 矩阵快速幂
mat pow_mat(mat a, LL n)
{
mat res = unit; // 初始为单位阵
while (n)
{
if (n & 1) res = res * a;
a = a * a;
n >>= 1;
}
return res;
}
mat dfs(int u) {
if (u == 1) return a; // 分治到1
if (u & 1) return dfs(u / 2) * (unit + pow_mat(a, u / 2)) + pow_mat(a, u); // 奇数
else return dfs(u / 2) * (unit + pow_mat(a, u / 2)); // 偶数
}
int main()
{
init_unit();
cin >> n >> k >> mod;
for (int i = 0; i < n; ++i)
for (int j = 0; j < n; ++j)
cin >> a.m[i][j];
mat res = dfs(k);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j)
cout << res.m[i][j] << " ";
cout << endl;
}
return 0;
}
acwing226 233矩阵
假设我们有一个名为233矩阵的矩阵。
在第一行,它将包含233,2333,23333 …(这意味着a0,1=233,a0,2=2333,a0,3=23333…)。
此外,在233矩阵中,满足ai,j=ai−1,j+ai,j−1(i,j≠0)。
现在给定a1,0,a2,0,…,an,0,请求出在233矩阵中an,m的值。
1≤n≤10,1≤m≤1e9,ai,0~int
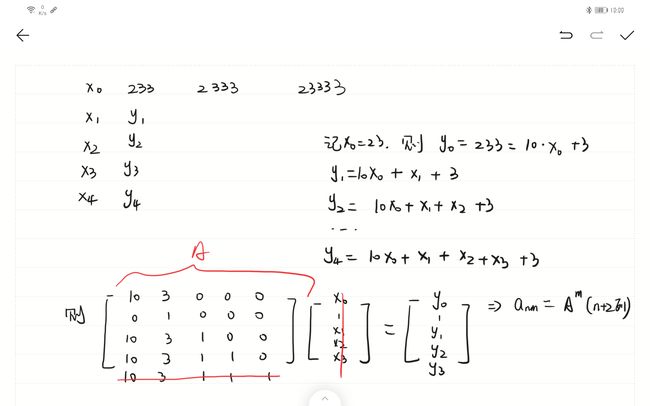
/*
233矩阵有特殊的特点
记x0=23
则y0=233=10x0+3
y1=10x0+x1+3
y2=10x0+x1+x2+3
y3=10x0+x1+x2+x3+3
...
yn=10x0+x1+x2+...+xn+3
那么可以矩阵快速幂求出每个y
*/
#include
using namespace std;
typedef long long LL;
const int N = 20, mod = 10000007;
int n, m;
int x[N];
// 定义一个矩阵
struct mat
{
int m[N][N];
}unit;
// 定义矩阵乘法
mat operator * (mat a, mat b)
{
mat res;
LL x;
for (int i = 0; i < n + 2; ++i)
for (int j = 0; j < n + 2; ++j)
{
x = 0;
for (int k = 0; k < n + 2; ++k)
x += (LL)a.m[i][k] * b.m[k][j] % mod;
res.m[i][j] = x % mod;
}
return res;
}
// 初始化单位阵
void init_unit()
{
for (int i = 0; i < N; ++i)
unit.m[i][i] = 1;
return ;
}
// 矩阵快速幂
mat pow_mat(mat a, LL n)
{
mat res = unit; // 初始为单位阵
while (n)
{
if (n & 1) res = res * a;
a = a * a;
n >>= 1;
}
return res;
}
int main()
{
init_unit();
while (scanf("%d%d", &n, &m) != EOF)
{
for (int i = 1; i <= n; ++i) scanf("%d", &x[i]);
mat a;
// 构造矩阵
for (int i = 0; i < n + 2; ++i){
if (i == 0) a.m[0][i] = 10;
else if (i == 1) a.m[0][i] = 3;
else a.m[0][i] = 0;
}
for (int i = 0; i < n + 2; ++i) {
if (i == 1) a.m[1][i] = 1;
else a.m[1][i] = 0;
}
for (int i = 2; i < n + 2; ++i) {
for (int j = 0; j < n + 2; ++j) {
if (j == 0) a.m[i][j] = 10;
else if (j == 1) a.m[i][j] = 3;
else if (j <= i) a.m[i][j] = 1;
else a.m[i][j] = 0;
}
}
// 计算矩阵的m次幂
a = pow_mat(a, m);
// 计算anm
LL res = (a.m[n + 1][0] * 23 + 0ll + a.m[n + 1][1] * 1) % mod;
for (int i = 1; i <= n; ++i) res = (res + 0ll + a.m[n + 1][i + 1] * 1ll * x[i] % mod) % mod;
cout << res << endl;
}
return 0;
}
3.2 斐波那契数列+矩阵快速幂
acwing1303斐波那契前n项和
求斐波那契数列fn的前n项和Sn mod m
n~2e9, m~1e9 + 10
/*
斐波那契数列可以使用矩阵快速幂来处理
设Fn={fn, fn+1, Sn}, Fn+1={fn+1, fn+2, Sn+1}
Fn+1=Fn * {0 1 0 = Fn * A = F1*A^n = {1, 1, 1} * A^n
1 1 1
0 0 1}
则Sn=Fn[3] = {1, 1, 1} * A ^(n - 1)
*/
#include
using namespace std;
typedef long long LL;
const int N = 110;
int n, m;
// 定义一个矩阵
struct mat
{
int m[N][N];
}unit;
// 定义矩阵乘法
mat operator * (mat a, mat b)
{
mat res;
LL x;
for (int i = 0; i < 3; ++i)
for (int j = 0; j < 3; ++j)
{
x = 0;
for (int k = 0; k < 3; ++k)
x += (LL)a.m[i][k] * b.m[k][j] % m;
res.m[i][j] = x % m;
}
return res;
}
// 初始化单位阵
void init_unit()
{
for (int i = 0; i < 3; ++i)
unit.m[i][i] = 1;
return ;
}
// 矩阵快速幂
mat pow_mat(mat a, LL n)
{
mat res = unit; // 初始为单位阵
while (n)
{
if (n & 1) res = res * a;
a = a * a;
n >>= 1;
}
return res;
}
int main()
{
init_unit();
cin >> n >> m;
int f[] = {1, 1, 1}; // F1
mat a;
int matrix[] = {0, 1, 0, 1, 1, 1, 0, 0, 1};
for (int i = 0; i < 3; ++i)
for (int j = 0; j < 3; ++j)
a.m[i][j] = matrix[i * 3 + j];
mat res = pow_mat(a, n - 1); // A^(n - 1)
// 计算Fn[2]
int ans = 0;
for (int i = 0; i < 3; ++i)
ans = (ans + res.m[i][2] * f[i]) % m;
cout << ans << endl;
return 0;
}
acwing1304佳佳的斐波那契
用 T(n)=(F1+2F2+3F3+…+nFn)modm 表示 Fibonacci 数列前 n 项变形后的和 modm 的值。
现在佳佳告诉你了一个 n 和 m,请求出 T(n) 的值。
n,m~int
/*
本题Sn = F1 + F2 + ... + Fn, Tn= F1 + 2F2 + ... + nFn,其中Sn为n级别,Tn为n方级别
那么考虑处理的时候Pn=nSn-Tn=(n-1)F1+(n-2)F2+...+Fn-1+0, Pn-1=(n-1)Sn-1 - Tn-1 = (n-2)F1 + (n-3)F2 + ... + Fn-2+0+0
则Pn=Pn-1+Sn-1,而Sn=Sn-1+Fn, Fn=Fn-1+Fn-2,当出现这种没有系数的式子时就可以转化为矩阵乘法:
则设Kn={fn, fn+1, Sn, Pn}, Kn-1={fn-1, fn, Sn-1, Pn-1}
Kn = Kn-1{ 0 1 0 0 = Kn-1 * A = K1 * A^(n - 1) = {1 ,1 ,1, 0} * A ^ (n - 1)
1 1 1 0
0 0 1 1
0 0 0 1}
记x = {1 ,1 ,1, 0} * A ^ (n - 1)
那么要求Tn=nSn - Pn=n*x[2] - x[3]
*/
#include
using namespace std;
typedef long long LL;
const int N = 110;
int n, m;
// 定义一个矩阵
struct mat
{
int m[N][N];
}unit;
// 定义矩阵乘法
mat operator * (mat a, mat b)
{
mat res;
LL x;
for (int i = 0; i < 4; ++i)
for (int j = 0; j < 4; ++j)
{
x = 0;
for (int k = 0; k < 4; ++k)
x += (LL)a.m[i][k] * b.m[k][j] % m;
res.m[i][j] = x % m;
}
return res;
}
// 初始化单位阵
void init_unit()
{
for (int i = 0; i < 4; ++i)
unit.m[i][i] = 1;
return ;
}
// 矩阵快速幂
mat pow_mat(mat a, LL n)
{
mat res = unit; // 初始为单位阵
while (n)
{
if (n & 1) res = res * a;
a = a * a;
n >>= 1;
}
return res;
}
int main()
{
init_unit();
cin >> n >> m;
int f[] = {1, 1, 1, 0};
mat a;
int matrix[] = {0, 1, 0, 0, 1, 1, 1, 0, 0 ,0, 1, 1, 0, 0, 0, 1};
for (int i = 0; i < 4; ++i)
for (int j = 0; j < 4; ++j)
a.m[i][j] = matrix[i * 4 + j];
mat res = pow_mat(a, n - 1);
int Sn = 0, Pn = 0;
for (int i = 0; i < 4; ++i)
Sn = (Sn + res.m[i][2] * f[i]) % m, Pn = (Pn + res.m[i][3] * f[i]) % m;
// cout << (LL)n * Sn % m << endl << Pn % m << endl;
cout << (((LL)n * Sn % m - Pn % m + m) % m + m ) % m<< endl;
return 0;
}