统计推断——假设检验——简单线性回归分析
一、线性回归描述
• 父亲身高与儿子身高存在相关（相关关系）
• 可否通过父亲身高预测儿子的身高？
• 新生儿的体重与体表面积存在相关
• 可否通过体重预测体表面积？（依存关系）
1、概述
例 为研究大气污染物一氧化氮（NO）的浓度是否受到汽车流量、气候状况等因素的影响，选择24个工业水平相近的城市的一个交通点，统计单位时间过往的汽车数（千辆）、同时在低空的相同高度测定了该时间段平均气温（℃）、空气湿度（%）、风速（m/s）以及空气
中一氧化氮（NO）的浓度（ppm），数据如表所示。
研究目的
• 通过探讨与一氧化氮（NO）浓度相关的影响因素，为控制空气污染提供依据。
• 研究一个变量的变化（如空气中NO浓度）受到另外一个或一些变量（如车流量）变化的制约。这些问题在统计学中采用线性回归模型（linear regression model）来进行分析。
基本概念
• 回归分析中，若
随
， 
,…，
的改变而改变，则称为反应变量（response variable），又称为因变量（dependent
variable）；
• ， ,…， 为解释变量（explanatory variable），又称为自变量（independent variable），通常我们把自变量看作影响
因素（factors）。
• 简单线性回归（simple linear regression）——自变量个数仅一个
• 多重线性回归（multiple linear regression）——自变量个数超过两个
• 
可以是随机变量，也可以是人为选择的数值
• 是按某种规律变化的连续型随机变量
2、简单线性回归模型
例，只考虑NO浓度与车流量的关系，以NO浓度为因变量，车流量为自变量，采用线性回归分析。问题如下：
问题
1. NO浓度随车流量的增加而增加吗？——散点图
2. 是直线趋势还是曲线趋势？——散点图
3. 如何采用回归方程定量地描述车流量对大气中NO浓度的影响？——线性回归方程
4. 车流量每增加100辆，NO浓度平均会增加多少？——回归方程的b值（回归系数）
5. 车流量对NO浓度的影响有统计学意义吗？——假设检验
6. 车流量对NO浓度的影响（贡献）有多大？——决定系数
7. 如何由车流量预测大气中NO平均浓度？——个体的容许区间、均数的置信区间
8. 如何通过控制车流量达到控制空气中NO浓度的目的？——根据求得的回归方程和给定的Y-hat值，求X值。
散点图
简单线性回归方程
以下为总体的线性回归方程，
表示在给定的X数值的情况下，Y值的总体平均水平。
回归系数的含义
的统计学意义是每增加（或减少）一个单位，平均改变个单位(即的均数改变个单位)。越大表示随增减变化的趋势越陡。
的意义
>0，表明与呈同向线性变化趋势；
<0，表明与呈反向线性变化趋势；
=0，表明与无线性回归关系，但并不表明没有其它关系。
样本的回归方程
基于样本的信息和数据建立的回归方程我们称为样本的回归方程。如下图，
表示刚才总体回归方程当中
的一个估计值，也就是当X指定一个数值的时候的平均水平的估计值，
和
分别代表样本的截距和样本的回归系数，如果在方程的左边用个体的观察值，那么在它的等号的右边就要加上一个残差项
，残差等于实际观察值与回归方程的相减，它在理论上服从均数为0，标准差为
的正态分布。
最小二乘估计
1. 最小二乘估计（least square estimation，LSE）
2. 其想法是找一条直线，使得实测点至该直线的纵向距离（即残差）的平方和最小，此平方和称为残差平方和，记为 
。残差平方和越小，该直线对散点趋势的代表性越好。
a 和 b 的计算
分子为X和Y的离均差的积和，分母为X的离均差的平方和。
注意：b的公式可以转化为如下公式：
二、线性回归的假设检验
回归方程有统计学意义吗？（在总体看来在和之间是否同样具有如下的线性关系）
• 假设检验包括两个方面：
1. 回归模型是否成立（model test）：方差分析（F检验）
2. 总体回归系数（包括斜率和截距）是否为零（parameter test）：
检验。
3.残差分析：D-W检验
在简单线性模型当中，由于仅仅包含一个自变量，所以对回归模型是否成立的假设检验和总体回归系数是否为零的假设检验是等价的，涉及到多元回归方程，则t检验不再适用。
1、回归模型的假设检验:
①回归模型检验的思想
总变异的分解-1
下图中，P表示某一个观察点。
总变异的分解-2
注意：
回归即自变量（方程的元）的个数。
中心思想：相比较残差的变异，回归的变异比重很大的话，说明回归是有意义的。
②回归模型假设检验的步骤
：总体回归方程不成立或总体中自变量对因变量没有贡献
：总体回归方程成立或总体中自变量对因变量有贡献
=0.05
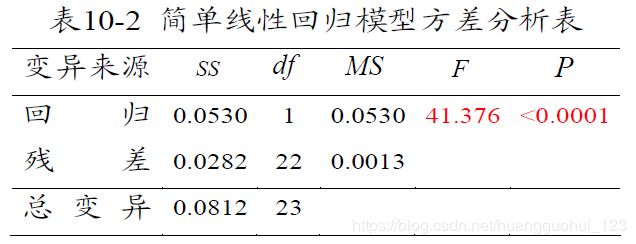
对例的回归方程 
进行方差分析，结果如表所示（假设检验步骤略）。
由表首行末列可见，
<0.0001，按=0.05 水准，可认为 NO 浓度与车流量之间的回归方程具有统计学意义。
2、回归系数的假设检验:
①对系数（b）的检验
对系数检验的步骤
：＝0
：
=0.05
下面式子b-0，是因为在H0成立的情况下，我们假定总体的回归系数等于0，b表示样本的回归系数，
表示回归系数的标准误，
表示在扣除X的影响下，Y剩余部分的标准差，也叫残差的标准差。
接上例，经计算得（假设检验步骤略）：
等于0.1584，
，且在一元线性回归模型当中，
。
由统计量得 <0.0001，按=0.05水准，拒绝，故可认为该回归系数具有统计学意义。
注意：对于服从双变量正态分布的同样一组资料，若同时做了相关分析和回归分析，则相关系数的检验与回归系数的检验等价，且 
。
总体回归系数的区间估计：
②对常数项（a）的检验
对常数项检验的步骤
：
＝0
：
=0.05
在H0成立的情况下，我们假定总体的常数项等于0，a表示样本的回归系数，表示回归常数项的标准误，表示在扣除X的影响下，Y剩余部分的标准差，也叫残差的标准差。
接上例，经计算得（假设检验步骤略）：
，
，
，
，
。
由统计量得 <0.05，按=0.05水准，拒绝，故可认为该回归常数项具有统计学意义。
当然，一般不以检验决定常数项是否保留在模型中，而是从应用的实际意义方面分析回归线是否应该通过原点，然后决定常数项的去留。
3、残差分析
4、回归直线的拟合优度（车流量对NO浓度的影响有多大？）
一元线性回归模型的决定系数和自变量、因变量的相关系数的关系：
如果判定系数太小，则说明自变量对因变量的线性解释程度太小，即模型的现实意义不大，可以考虑使用别的分析方法进行分析，或者使用多元性回归和曲线回归的方法。
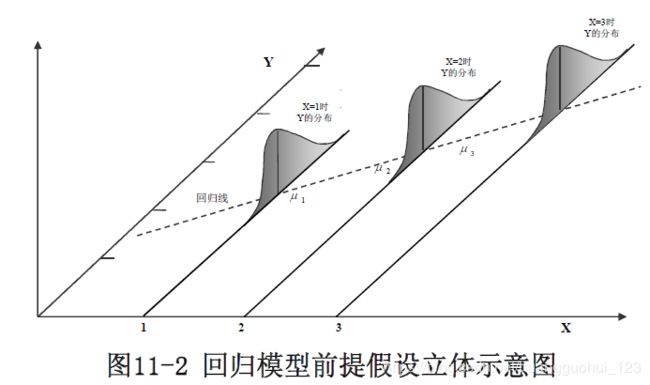
线性回归分析的前提条件：LINE
1. 线性（linear）：反应变量与自变量的呈线性变化趋势。
2. 独立性（independence）：任意两个观察值相互独立，一个个体的取值不受其他个体的影响。
3. 正态性（normal distribution）：在给定值时，的取值服从正态分布
4. 等方差性（equal variance）: 对应于不同的 值，值的总体变异相同 。
三、简单线性回归的应用
问题
1. NO浓度随车流量的增加而增加吗？
2. 是直线趋势还是曲线趋势？
3. 如何采用回归方程定量地描述车流量对大气中NO浓度的影响？
4. 车流量每增加100辆，NO浓度平均会增加多少？
5. 车流量对NO浓度的影响有统计学意义吗？
6. 车流量对NO浓度的影响（贡献）有多大？
7. 如何由车流量预测大气中NO平均浓度？
8. 如何通过控制车流量达到控制空气中NO浓度的目的？
统计应用
统计预测
个体的容许区间： 预测是回归分析的重要应用之一，医学上常用在给定值（预报因子）时，计算个体值的容许区间。所谓个体值的容许区间是指总体中为某定值时，个体值的波动范围。
表示给定的的数值。
当车流量为1300辆时，
，
空气中一氧化氮95%容许区间为
当车流量为1300辆时，大气中NO浓度的水平是存在变异的，大概95%的观察值分布的范围是从0到0.1467ppm。
均数的置信区间： 当为某定值和在给定置信度的情况下，欲知的总体均数的分布如何？我们可以估计总体中当为某定值
时，的总体均数
的
置信区间 。
当车流量为1300辆时，，
空气中一氧化氮95%置信区间为
当车流量为1300辆时，大气中NO浓度的总体的平均水平应该在0.05465到0.08675ppm。
统计控制
根据空气污染指数分级，当空气质量状况不超过级时，要求空气中氮氧化物含量不超过0.100ppm～0.150ppm。该城市为降低空气中NO的含量，拟对车流量做适当控制。
依据估计的回归方程
和以上标准，分别计算得：
时，
(千辆)
时，
(千辆)
该城市单位时间内车流量应控制在 1500 辆以内，超过此限可能导致轻度污染；当车流量大于 1800 辆时，可能导致空气中度污染。
结果报告
• 简单线性回归分析通常需要报告以下内容：
1. 分析目的；
2. 拟合简单线性回归方程的估计方法；
3. 是否符合前提条件（LINE）；
4. 参数估计结果；
5. 模型的拟合优度及其假设检验；
6. 对结果的专业解释。