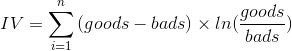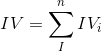IBM SPSS Modeler案例：信用风险评分方法

        在现代社会中，信用对个人和企业都是无比重要的品质。无论是办理信用卡业务，开通国际长途业务，还是获取大额融资额度，都跟你的信用级别挂钩。那么应该如何评价个人或者企业的信用情况？也许可以使用决策树或者神经网络等算法 ，但实际上，数据分析员可以理解与接受，但是广大业务人员却不甚了解。现在银行业比较通用的方法是使用信用评分的形式。

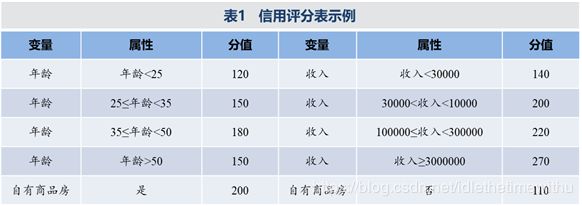
        信用评分是使用统计模型的方法对潜在客户和已有客户在贷款（包括信用卡）时的风险通过评分卡的方式进行评价的一种方法。信用评分卡的形式如下表所示（为简单起见，这里只选择三个变量作为示例）。

1. 什么是信用风险

信用风险：交易对手未能履行约定契约中的义务而造成经济损失的风险，即受信人不能履行还本付息的责任而使授信人的预期收益与实际收益发生偏离的可能性它是金融风险的主要类型。

2. 坏样本的定义

把能够按期归还的贷款账户理解为“好”的信贷账户，对应的客户为“好”客户；把不能按期归还的贷款账户理解为“坏”的信贷账户，对应的客户为“坏”客户。根据业务经验来看，欠还贷按照拖欠期长短可以分为：拖欠少于30天(1个月)，31天-60天(2个月)、61天-90天(3个月)……拖欠180天以上的基本可以认为是坏账。应该选择哪种情况作为“坏”的定义呢?

•  如果银行的目的是为了扩大市场占有率，这个时候往往对坏账率有较强的容忍度，这个时候就可以把“坏”定义为拖欠期更长一些，比如3个月以上拖欠才定义为坏。
•   如果银行业务发展稳定，意图是扩大利润，尽可能减少坏账率的发生，这个时候就可以把“坏”定义为拖欠期短一些，例如1个月以上拖欠即定义为“坏”。
•  另外，如果定义了3个月拖欠为“坏”，那么不拖欠、拖欠1个月和拖欠两个月的客户的信用情况显然有相当的差异对它们同等对待似乎不大公平。如果发现数据中拖欠1-2个月的客户比例不是特别大，可以删除这部分数据，不进入后面的建模过程。

经过以上讨论，可以采取这样的定义来确定目标变量一信贷账户是否违约：表现期内未拖欠为好，3个月及以上拖欠为坏，1-2个月拖欠数据删除不用。 

3. 数据获取

信用评分从类别上看可以分为申请评分与行为评分。其中申请评分是指对贷款(或者信用卡)申请人(或者企业)的资信情况进行评估并预测其未来违约可能性的模型。行为评分是指对已经发放贷款(或者信用卡)的个人(或者企业)所表现出来的各种行为特征来预测其未来的贷款偿还表现的模型。

• 对申请评分来说；预测自变量的数据来源主要是信贷申请人在申请贷款(或者信用卡时所提交的申请资料。预测目标变量的取值可以根据前面所讨论的按照贷款人的实际拖欠行为进行判断。
• 对于行为评分来说，除了获取贷款人在申请时提交的各种信息，还可以从系统中获取大量关于贷款人(信用卡持有人)的资金使用，消费以及还款情况数据。这些数据包括(但不限于)以下变量：账户存在时间；过去12个月最严重的拖欠行为；过去12个月的平均贷款余额；过去6个月的还款占欠款比例；过去6个月平均消费额；过去6个月消费类型等

4.  评分卡开发模型

4.1  数据准备（不平衡样本处理）

在信贷数据中，违约客户所占比例较少，一般不会超过3%~5%。在数据正负样本不均衡情况下，当然正负样本不要求1:1，但是也不能太大。假如正负样本比例 1:10，把这样不均衡的数据直接放进模型中进行训练，准确率会很高，因为大部分都可以预测为负样本。但是训练出的模型泛化能力很弱。这时需要对数据进行采样，使得数据样本均衡。通常有四种办法来进行采样：①从负样本中抽取部分样本出来和正样本结合；②正样本重复若干次；③SMOTE(原理及实现)；④代价敏感学习

在本次实验中，在选取建模数据时可以采取分层抽样方法来构成建模样本。例如，某银行有100个小额贷款账户，根据182节的定义，“坏”的比例为3%，即有97万个“好”账户，有3万个“坏”账户。为了建立模型，从中抽取1万个账户构成样本。为了使所抽取的样本能够反映总体的违约情况比例，且建模样本数据中“坏”客户比例不至于过低而影响建模效果，我们可以从“好”账户里抽取5000个账户进入建模样本，这时“好”账户的样本权重为970000/5000=194，即建模数据中每个账户代表总体中的194个“好”账户；从“坏”账户里也抽取5000个账户进入建模样本，“坏”账户的样本权重为30000/5000=6，即建模数据中每个账户代表总体中的6个“坏”账户。（体现为“权重”变量）

在极端情况下，如果“坏”账户比例很低或者绝对数很少，甚至可以取全部“坏”账户和一定比例的“好”账户进入建模数据。

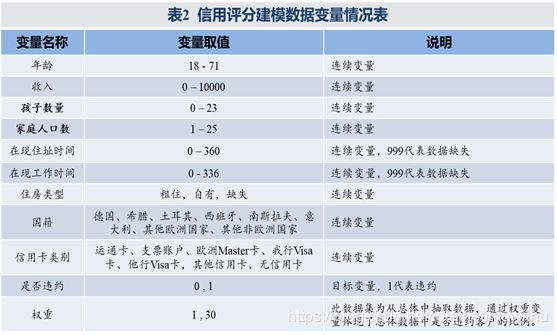
观察数据可得：孩子数量与家庭人口数之间相关性很强，经过计算相关四叔，可以得到两个变量之间的相关系数达到0.949，在建模时只保留一个变量。这里选择保留孩子数量变量。

4.2  建立模型与模型评估

• 步骤一：输入变量的分箱。
• 步骤二：建立输入变量与目标变量的Logistic回归模型。
• 步骤三：根据相关业务参数将Logistic回归模型转换为评分模型。
• 步骤四：对模型效果进行检验。

4.2.1 信用评分方法中的变量分箱

（1）连续变量分箱：从总体上看，分箱是一个和具体业务问题结合紧密的工作，并不存在标准答案。通常，在分箱时应该遵循以下基本原则。

• 原则一：分箱数应当适中，不宜过多或过少。过少区分度不足，过多则稳定性不强且不方便管理。
• 原则二：各个分箱内的记录数合理，不应过多或过少。
• 原则三：结合目标变量，分箱应该能表现出明显的趋势特征。
• 原则四：相邻分箱的目标变量分布差异应该较大

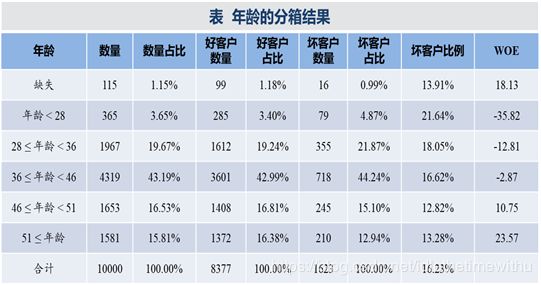
为了帮助分箱，通常采取下表所示的方式计算各种统计量，并据此判断变量对预测目标变量是否重要以及分箱是否合理。该表仅供示例，所有数字均为随机生成，不具有实示业务含义。

• 数量：指该分箱内包含的记录个数。
• 数量占比：指该分箱内包含记录数量占总记录数量的比例。
• 不违约数量：指该分箱内包含的不违约客户数量，即好客户数量。
• 未违约占比：分箱内包含好客户数量占全部好客户数量的比例，记goods。
• 违约数量：指该分箱内包含的违约客户数量，即坏客户数量。
• 违约占比：分箱内包含坏客户数量占全部好客户数量的比例，记bads。
• 违约比例：指该分箱内包含的坏客户数量占该分箱内全部客户数量的比例。
• WOE：证据权重(Weight of Evidence)。根据好客户占比和坏客户占比计算得到的，与违约比例同方向变动。该变量计算公式为：

进一步，可根据WOE值，还可以计算IV值，即信息值（Information Value），IV值得计算公式为：

注解：IV的全称是Information Value，中文意思是信息价值，或者信息量。IV可以用来衡量自变量的预测能力。类似的指标还有信息增益、基尼系数等等。

对于一个分组 ，会有一个对应的IV值，计算公式为：

有了一个变量各分组的IV值，我们就可以计算整个变量的IV值，方法很简单，就是把各分组的IV相加：

                其中，n为变量分组个数。

信息值IV可用来表示该变量是否对预测目标变量具有显著意义。根据经验：

1. 当IV < 0.02时，该变量对预测目标变量几乎没有帮助
2. 当0.02 ≤ IV < 0.1时，该变量对预测目标变量具有一定帮助
3. 当0.1 ≤ IV < 0.3时，该变量对预测目标变量具有较大帮助
4. 当0.3 ≤ IV时，该变量对预测目标变量具有很大帮助

请注意，当Ⅳ=0.5时，该变量对目标变量有过度预测的倾向，应该仔细检查看看是不是选用了和目标变量有很强因果关系的变量，这种变量是否可用于预测模型。

（2）离散变量分箱

在离散变量取值较少的情况下，不需要对之进行处理。当离散变量取值较多的时候，为了管理方便，可以按照WOE值接近的原则，将离散变量若干类别。

（3）具体操作

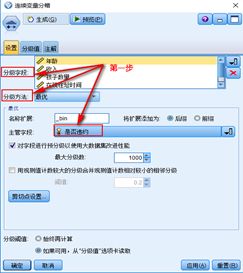
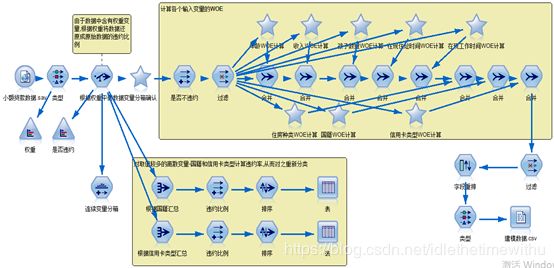
对于连续变量，在 IBM SPSS Modeler中有专门的分箱节点，其中包含了最优分箱方法。使用此方法，需要设置一个离散的目标变量。设置了目标变量后，该节点会根据该目标变量的分布情况，对指定的连续型输入变量进行分箱，继而可以选择导出将连续变量分箱结果生成新的变量。以年龄分箱为例，具体实现步骤如下图所示。对于离散变量取值较多的情况，在 IBM SPSS Modeler中，可以按照WOE值接近的原则，使用重新分类节点对离散变量重新进行分箱处理。具体步骤为：

① 步骤一：在分箱节点中选择分箱方法为最优，主管字段选择为是否违约。

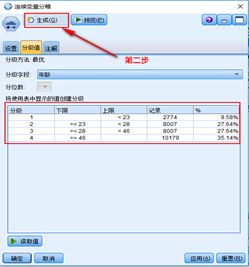
②步骤二：选择生成--> 导出。

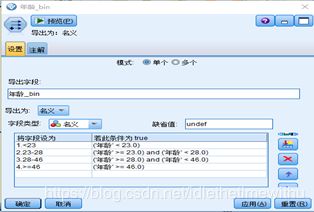
③步骤三：在导出字段中将字段取值修改为容易识别的形式。

                   

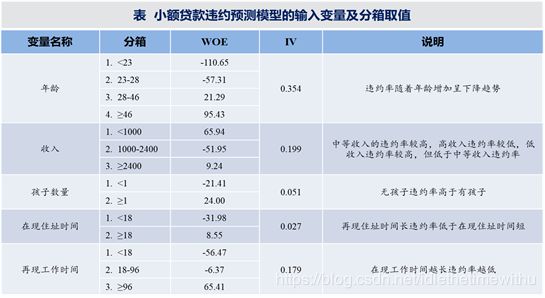
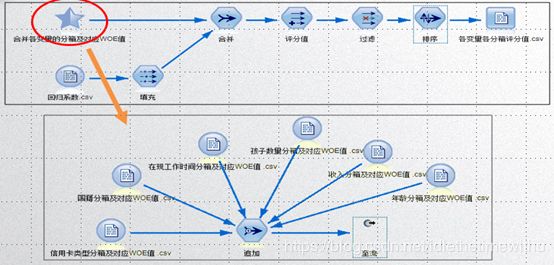
 对所有变量进行分箱以后，可以按照下图所示的数据流计算各个变量的Ⅳ值及各个分箱的WOE值。运行分箱及生成WOE值数据流可以得到下表所示的结果。

               

从中可以看出各个变量的分箱情况及分箱对应的WOE值，另外还得到了评价变量重要程度的Ⅳ信息值，根据前面统计知识介绍的经验规则可以看出，其中住房类型Ⅳ值仅为008，说明该变量对预测是否违约作用并不大，可以在后面的建模过程中剔除该变量。

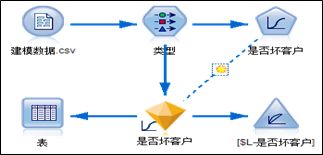
4.2.2 用Logistic回归建立信用预测模型

逻辑回归的模型表示为：

一般情况下，输入变量主要为连续变量，当输入变量为离散变量时，通常采取哑变量的方式将离散变量转化为连续变量再进行处理。但是在构建信用评分卡时，由于所有变量都已经被转化为离散变量，这时如果把全部离散变量都转化为哑变量，会丢失很多信息，因为使用哑变量会认为相邻的两个变量取值(两个分箱)之间的差异相同的，这显然不符合实际情况。作为替代，通常使用各个变量分箱对应的WOE值作为 Logistic回归的输入变量，这样做充分考虑了不同分箱之间的差异，同时也保留了各变量对目标变量分布的趋势。

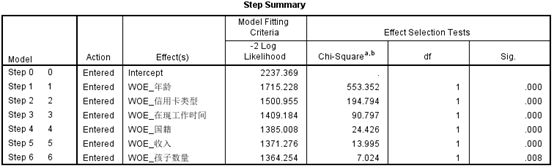
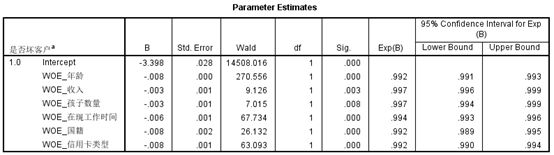
从逐步回归分析过程中只有6个变量进入模型，剔除了变量“在现住址时间”：

可以看出各个变量的回归系数及常数项：

4.2.3 生成信用评分模型

（1）如何将Logistic回归系数转化为信用评分？

将Logistic回归系数转化为信用评分其实是一个量表编制的过程。为方便业务人员使用，使评分之间的差异具有业务含义，通常希望生成的评分能满足以下三要求：

① 将评分控制在一定范围内，例如0-1000分之间。（美国FICO评分位于300-850之间）

② 在特定分数时，好客户和坏客户具有一定的比例关系.。 (在统计学上用一个专门的统计量——优比 ( odds来表示这种比例关系， ）， 例如希望在评分值为500分的时候好客户和坏客户的比例为50:1。

③ 评分值的增加应该能够反映好客户和坏客户比例关系的变化。例如希望当评分值每增加50分时，odds也增加一倍。

（2）比较通用的表示信用评分取值关系的方程如下：

为了满足以上3个条件，该方程需要满足如下两个等式：

 

其中： (point to double the odds)  表示为了使odds增加一倍需要增加的评分值

解（1）,（2）方程得：      即：   ,  

如果取评分值为500时odds为30：1，且评分值每增加50分时，odds增加一倍，则有：

从而得到最终评分方程式：

又因为逻辑回归中有：     代入上面公式，得到：

        

其中，WOE代表各个变量i的各个分箱j的WOE值， α，β代表Logistic回归结果的各个系数，n代表输入变量的数量，k代表各个输入变量的分箱数。需要注意到的是：回归方程前面更改为负号是因为在Logistic回归中使用的odds分子是坏客户的比例，而这里的odd分子是好客户的比例。

通过以上介绍，可以通过如下的变换得到每个变量的，因此每个睡醒对应的分值为：

属性对应评分值 = 

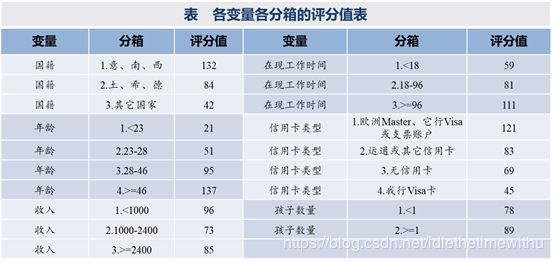
 这样就得到了各个变量分箱对应的评分值，如下表：

4.2.4 模型检验

（1）用K-S指标法检验目标变量为标志变量的预测模型

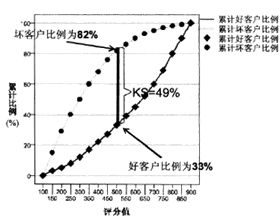
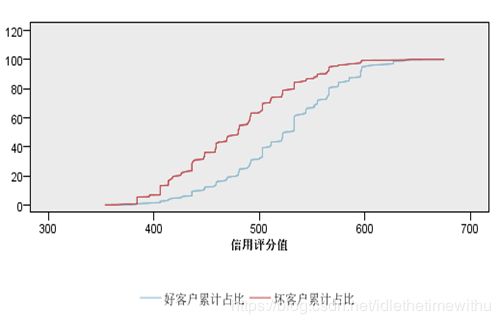
K-S指标是根据两位统计学家 Kolmogorov和 Smirnoff命名的一种模型检验方法。它用下图所示的形式来对目标变量为标志变量的预测模型效果进行检验。图中横坐标代表信用评分值，按照从小到大的顺序排列，纵坐标代表累计百分比。两条曲线分别代表对应评分值处好客户累计占比和坏客户累计占比。在模型有效的情况下，坏客户累计占比曲线应该在好客户累计占比曲线之上，且这两条曲线距离越远，则模型效果越好，模型区分好客户和坏客户的能力越强。

例如，在信用评分为500分时，两条曲线的距离最大，其中坏客户累计占比达到了82%，而好客户累计占比为33%。这代表如果把500分作为拒绝贷款的临界点，500分以上同意发放贷款，500分以下拒绝发放贷款，则会拒绝82%的坏客户，舍弃了33%的好客户，在500分处K-S指标值为0.49。一般认为区分度在30%以上的模型是可以接受的。

在 IBM SPSS Modeler中，没有直接作出K-S指标及图形的节点，但是可以通过节点的组合生成K-S指标和相关图形，具体数据流如图18.13所示，图18.14是产生的K-S图。通过对K-S指标的观察可以发现，当信用评分值为492时K-S值最大，这时坏客户占比为63333%，而好客户占比为31.267%，K-S=32.067%，即如果把拒绝贷款的临界点选择为492分，这时会拒绝63.3%的坏客户，同时也会舍弃33%的好客户。