数据科学 案例2 统计推断基础之房价预测（代码）

第6讲 统计推断基础

• 数据说明：本数据是地区房价增长率数据
• 名称-中文含义
• dis_name-小区名称
• rate-房价同比增长率

import os
# os.chdir(r"D:\Python_Training\script_Python\6inference")
import pandas as pd

house_price_gr = pd.read_csv(r'.\data\house_price_gr.csv', encoding='gbk')
house_price_gr.head()

	dis_name	rate
0	东城区甘南小区	0.169747
1	东城区察慈小区	0.165484
2	东城区胡家园小区	0.141358
3	东城区台基厂小区	0.063197
4	东城区青年湖小区	0.101528

6.1 参数估计

1、进行描述性统计分析

house_price_gr.describe(include='all')

	dis_name	rate
count	150	150.000000
unique	150	NaN
top	怀柔区迎宾北路12号院	NaN
freq	1	NaN
mean	NaN	0.110061
std	NaN	0.041333
min	NaN	0.029540
25%	NaN	0.080027
50%	NaN	0.104908
75%	NaN	0.140066
max	NaN	0.243743

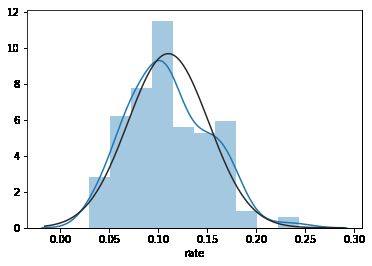
直方图

在统计学中，QQ图 是一种通过比较两个概率分布的分位数对这两个概率分布进行比较的概率图方法。首先选定分位数的对应概率区间集合，在此概率区间上，点对应于第一个分布的一个分位数x和第二个分布在和x相同概率区间上相同的分位数。因此画出的是一条含参数的曲线，参数为概率区间的分割数。

get_ipython().magic('matplotlib inline')
import seaborn as sns
from scipy import stats
# sns.distplot(house_price_gr.rate,kde=False,fit=stats.norm)
sns.distplot(house_price_gr.rate,kde=True,fit=stats.norm)

蓝线和黑线完全重合：表示服从正态分布

import statsmodels.api as sm
from matplotlib import pyplot as plt

fig = sm.qqplot(house_price_gr.rate, fit=True, line='45')
fig.show()
# Box Plots
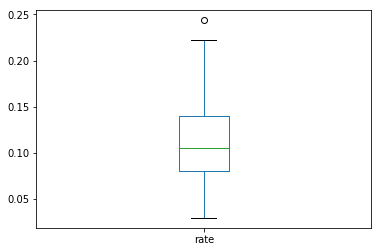
house_price_gr.plot(kind='box') # Box Plots

蓝线与红线完全重合表示服从正态分布

2、置信度区间估计

为什么是1.96？
$P$($\mu$−1.96$\frac{\sigma }{\sqrt{n}}$$\mu$+1.96$\frac{\sigma }{\sqrt{n}}$)=0.95

1、法一（直接计算）

se = house_price_gr.rate.std() / len(house_price_gr) ** 0.5 #均值标准误差
LB = house_price_gr.rate.mean() - 1.96 * se #置信区间下界
UB = house_price_gr.rate.mean() + 1.96 * se #置信区间上界
(LB, UB)

(0.10344632517993363, 0.11667566822391268)

2、法二（定义函数计算）

# 如果要求任意置信度下的置信区间的话，可以自己编一个函数
def confint(x, alpha=0.05):
    n = len(x)
    xb = x.mean()
    df = n-1
    tmp = (x.std() / n ** 0.5) * stats.t.ppf(1-alpha/2, df)
    return {'Mean': xb, 'Degree of Freedom':df, 'LB':xb-tmp, 'UB':xb+tmp}

confint(house_price_gr.rate, 0.05)

{'Mean': 0.11006099670192315,
 'Degree of Freedom': 149,
 'LB': 0.10339228338892809,
 'UB': 0.11672971001491822}

3、法三（直接调用函数）

# 或者使用DescrStatsW
d1 = sm.stats.DescrStatsW(house_price_gr.rate)
d1.tconfint_mean(0.05) # 

(0.10339228338892814, 0.11672971001491828)

6.2 假设检验与单样本T检验

当年住宅价格的增长率是否超过了10%的阈值

d1 = sm.stats.DescrStatsW(house_price_gr.rate)
print('t-statistic=%6.4f, p-value=%6.4f, df=%s' %d1.ttest_mean(0.1))

t-statistic=2.9812, p-value=0.0034, df=149.0

6.3 两样本T检验

（二分类与连续变量做两样本t检验）

导入数据
数据说明：本数据是一份汽车贷款数据

字段名	中文含义
id	id
Acc	是否开卡(1=已开通)
avg_exp	月均信用卡支出（元）
avg_exp_ln	月均信用卡支出的自然对数
gender	性别(男=1)
Age	年龄
Income	年收入（万元）
Ownrent	是否自有住房（有=1；无=0)
Selfempl	是否自谋职业(1=yes, 0=no)
dist_home_val	所住小区房屋均价(万元)
dist_avg_income	当地人均收入
high_avg	高出当地平均收入
edu_class	教育等级：小学及以下开通=0，中学=1，本科=2，研究生=3

creditcard= pd.read_csv(r'.\data\creditcard_exp.csv', skipinitialspace=True)
creditcard.head()

	id	Acc	avg_exp	avg_exp_ln	gender	Age	Income	Ownrent	Selfempl	dist_home_val	dist_avg_income	age2	high_avg	edu_class
0	19	1	1217.03	7.104169	1	40	16.03515	1	1	99.93	15.932789	1600	0.102361	3
1	5	1	1251.50	7.132098	1	32	15.84750	1	0	49.88	15.796316	1024	0.051184	2
2	95	0	NaN	NaN	1	36	8.40000	0	0	88.61	7.490000	1296	0.910000	1
3	86	1	856.57	6.752936	1	41	11.47285	1	0	16.10	11.275632	1681	0.197218	3
4	50	1	1321.83	7.186772	1	28	13.40915	1	0	100.39	13.346474	784	0.062676	2

creditcard.Acc.value_counts()

1    70
0    30
Name: Acc, dtype: int64

creditcard['Income'].groupby(creditcard['Acc']).describe()
# creditcard.groupby('Acc') ['Income'].describe()

	count	mean	std	min	25%	50%	75%	max
Acc
0	30.0	3.149333	1.406482	1.5000	2.285000	2.905000	3.807500	8.40000
1	70.0	7.424706	3.077986	3.4939	5.175662	6.443525	8.494237	16.90015

• 第一步:方差齐次检验（实际中，不需要管齐不齐）

Suc0 = creditcard[creditcard['Acc'] == 0]['Income']
Suc1 = creditcard[creditcard['Acc'] == 1]['Income']
leveneTestRes = stats.levene(Suc0, Suc1, center='median')
print('w-value=%6.4f, p-value=%6.4f' %leveneTestRes)

w-value=7.1829, p-value=0.0086

• 第二步:T-test（equal_var的取值不影响结论）

stats.stats.ttest_ind(Suc0, Suc1, equal_var=False)
# Or Try: sm.stats.ttest_ind(gender0, gender1, usevar='pooled')

Ttest_indResult(statistic=-9.529516968736448, pvalue=1.3263066753296544e-15)

#测试一下性别对是月均消费的作用.
#注意对缺失值得处理
creditcard['avg_exp'].groupby(creditcard['gender']).describe()
female= creditcard[creditcard['gender'] == 0]['avg_exp'].dropna()
male = creditcard[creditcard['gender'] == 1]['avg_exp'].dropna()
leveneTestRes = stats.levene(female, male, center='median')
print('w-value=%6.4f, p-value=%6.4f' %leveneTestRes)
stats.stats.ttest_ind(female, male, equal_var=True)

w-value=0.0683, p-value=0.7946
Ttest_indResult(statistic=-1.742901386808629, pvalue=0.08587122878448449)

6.4 方差分析

• 单因素方差分析

pd.set_option('display.max_columns', None) # 设置显示所有列
creditcard.groupby('edu_class')[['avg_exp']].describe().T

	edu_class	0	1	2	3
avg_exp	count	2.000000	23.000000	23.000000	22.000000
	mean	207.370000	641.937826	973.321304	1422.280909
	std	62.494097	147.577741	229.163196	435.281442
	min	163.180000	418.780000	610.250000	816.030000
	25%	185.275000	525.595000	807.820000	1166.997500
	50%	207.370000	593.920000	959.830000	1343.025000
	75%	229.465000	736.140000	1075.270000	1661.412500
	max	251.560000	987.660000	1472.820000	2430.030000

# 利用回归模型中的方差分析
import statsmodels.api as sm
from statsmodels.formula.api import ols
#edu_class是分类变量，所以前面加C
sm.stats.anova_lm(ols('avg_exp ~ C(edu_class)',data=creditcard).fit())

	df	sum_sq	mean_sq	F	PR(>F)
C(edu_class)	3.0	8.126056e+06	2.708685e+06	31.825683	7.658362e-13
Residual	66.0	5.617263e+06	8.511005e+04	NaN	NaN

• 多因素方差分析

#不考虑交互相
sm.stats.anova_lm(ols('avg_exp ~ C(edu_class)+C(gender)',data=creditcard).fit())

	df	sum_sq	mean_sq	F	PR(>F)
C(edu_class)	3.0	8.126056e+06	2.708685e+06	31.578365	1.031496e-12
C(gender)	1.0	4.178273e+04	4.178273e+04	0.487111	4.877082e-01
Residual	65.0	5.575481e+06	8.577662e+04	NaN	NaN

#考虑交互相
sm.stats.anova_lm(ols('avg_exp ~ C(edu_class)+C(gender)+C(edu_class)*C(gender)',data=creditcard).fit())

	df	sum_sq	mean_sq	F	PR(>F)
C(edu_class)	3.0	8.126056e+06	2.708685e+06	33.839350	3.753889e-13
C(gender)	1.0	4.178273e+04	4.178273e+04	0.521988	4.726685e-01
C(edu_class):C(gender)	3.0	8.761475e+05	2.920492e+05	3.648543	1.716862e-02
Residual	63.0	5.042862e+06	8.004544e+04	NaN	NaN

6.5 相关分析

# 散点图
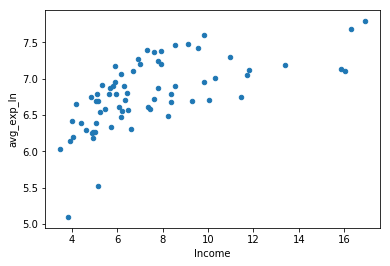
creditcard.plot(x='Income', y='avg_exp', kind='scatter')

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-BxqxQYgo-1581821143045)(output_35_1.png)]

#当发现散点图有发散的趋势时，首先需要对Y取对数，而且还应该尝试对X也取对数
creditcard.plot(x='Income', y='avg_exp_ln', kind='scatter')

• 相关性分析:“spearman”,“pearson” 和 “kendall”

creditcard[['avg_exp_ln', 'Income']].corr(method='pearson') #pearson/spearman/kendall
#import numpy as np
#creditcard['Income_ln']=np.log(creditcard['Income'])

	avg_exp_ln	Income
avg_exp_ln	1.00000	0.63489
Income	0.63489	1.00000

6.6卡方检验

cross_table = pd.crosstab(creditcard.edu_class, columns=creditcard.Acc)
# Or try this: accepts.pivot_table(index='bankruptcy_ind',columns='bad_ind', values='application_id', aggfunc='count')
cross_table

Acc	0	1
edu_class
0	16	2
1	14	23
2	0	23
3	0	22

cross_table_rowpct = cross_table.div(cross_table.sum(1),axis = 0)
cross_table_rowpct

Acc	0	1
edu_class
0	0.888889	0.111111
1	0.378378	0.621622
2	0.000000	1.000000
3	0.000000	1.000000

print('chisq = %6.4f\n p-value = %6.4f\n dof = %i\n expected_freq = %s'  %stats.chi2_contingency(cross_table))

chisq = 50.0930
 p-value = 0.0000
 dof = 3
 expected_freq = [[ 5.4 12.6]
 [11.1 25.9]
 [ 6.9 16.1]
 [ 6.6 15.4]]