大话数据结构十四：二叉树的顺序存储结构（数组实现）

1. 顺序存储结构：

二叉树的顺序存储结构就是用一维数组存储二叉树中的结点。

2. 完全二叉树：

完全二叉树由于其结构上的特点，通常采用顺序存储方式存储。一棵有n个结点的完全二叉树的所有结点从1到n编号，就得到结点的一个线性系列。

如下图：完全二叉树除最下面一层外，各层都被结点充满了，每一层结点的个数恰好是上一层结点个数的2倍，因此通过一个结点的编号就可以推知它的双亲结点及左，右孩子结点的编号：

①当 2i ≤ n 时，结点 i 的左孩子是 2i，否则结点i没有左孩子；

②当 2i+1 ≤ n 时，结点i的右孩子是 2i+1，否则结点i没有右孩子；

③当 i ≠ 1 时，结点i的双亲是结点 i/2；

注意：由于数组下标从0开始，因此数组元素的下标等于结点在完全二叉树中的序号减1。

3. 一般二叉树：

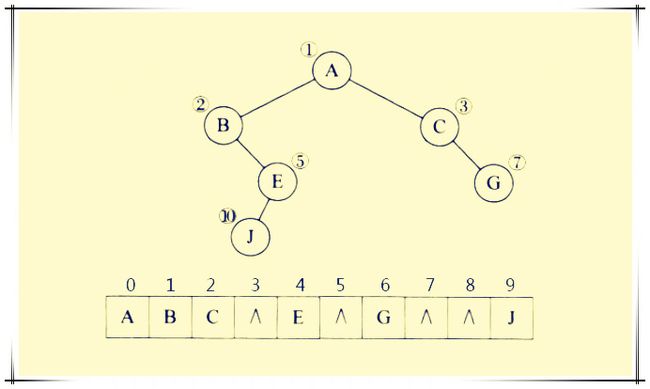
对于一般的二叉树，如果仍按照从上至下，从左到右的顺序将树中的结点顺序存储在一维数组中，则数组元素下标之间的关系不能够反映二叉树中结点之间的逻辑关系。

这时假设将一般二叉树进行改造，增添一些并不存在的空结点，使之成为一棵完全二叉树的形式，然后再用一维数组顺序存储。在二叉树中假设增添的结点在数组中所对应的元素值为"空"用^表示。

4. Java实现顺序存储：

public class ArrayBinaryTree {
	private Object[] arr; // 用数组来存储树的所有节点
	private int deep; // 保存该树的深度
	private int size; // 数组大小
	private static final int DEFAULT_DEEP = 5; // 树的默认深度

	/**
	 * 以默认的深度来创建二叉树
	 */
	public ArrayBinaryTree() {
		this.deep = DEFAULT_DEEP;
		this.size = (int) Math.pow(2, deep) - 1; // Math.pow(2,deep)返回第一个参数的第二个参数次幂的值
		arr = new Object[size];
	}

	/**
	 * 以指定深度来创建二叉树
	 * @param deep
	 */
	public ArrayBinaryTree(int deep) {
		this.deep = deep;
		this.size = (int) Math.pow(2, deep) - 1;
		arr = new Object[size];
	}

	/**
	 * 以指定深度,指定根节点创建二叉树
	 * 
	 * @param deep 树的深度
	 * @param data 数据
	 */
	public ArrayBinaryTree(int deep, T data) {
		this.deep = deep;
		this.size = (int) Math.pow(2, deep) - 1; 
		arr = new Object[size];
		arr[0] = data; // 根节点
	}

	/**
	 * 为指定节点添加子节点。
	 * 
	 * @param index 需要添加子节点的父节点的索引
	 * @param data 新子节点的数据
	 * @param left 是否为左节点
	 */
	public void add(int index, T data, boolean left) {
		if (arr[index] == null) {
			throw new RuntimeException(index + "处节点为空，无法添加子节点");
		}
		if (2 * index + 1 >= size) {
			throw new IndexOutOfBoundsException();
		}
		if (left) { 
			arr[2 * index + 1] = data; // 添加左子节点
		} else {
			arr[2 * index + 2] = data; // 添加右子结点
		}
	}

	/**
	 * 判断二叉树是否为空
	 * @return
	 */
	public boolean isEmpty() {
		return arr[0] == null; // 根据根元素来判断二叉树是否为空
	}

	/**
	 * 返回根节点
	 * @return
	 */
	@SuppressWarnings("unchecked")
	public T getRoot() {
		return (T) arr[0];
	}

	/**
	 * 返回指定节点（非根节点）的父节点
	 * @param index 
	 * @return
	 */
	@SuppressWarnings("unchecked")
	public T getParent(int index) {
		return (T) arr[(index - 1) / 2];
	}

	/**
	 * 返回指定节点（非叶子）的左子节点，当左子节点不存在时返回null
	 * @param index
	 * @return
	 */
	@SuppressWarnings("unchecked")
	public T getLeft(int index) {
		if (2 * index + 1 >= size) {
			throw new RuntimeException("该节点为叶子节点，无子节点");
		}
		return (T) arr[index * 2 + 1];
	}

	/**
	 * 返回指定节点（非叶子）的右子节点，当右子节点不存在时返回null
	 * @param index
	 * @return
	 */
	@SuppressWarnings("unchecked")
	public T getRight(int index) {
		if (2 * index + 1 >= size) {
			throw new RuntimeException("该节点为叶子节点，无子节点");
		}
		return (T) arr[index * 2 + 2];
	}

	/**
	 * 返回该二叉树的深度。
	 * @param index
	 * @return
	 */
	public int getDeep(int index) {
		return deep;
	}

	/**
	 * 返回指定节点的位置。
	 * @param data
	 * @return
	 */
	public int index(T data) {
		for (int i = 0; i < size; i++) { // 该循环实际上就是按广度遍历来搜索每个节点
			if (arr[i].equals(data)) {
				return i;
			}
		}
		return -1;
	}
	
	/**
	 * 打印数组
	 */
	public String toString() {
		return Arrays.toString(arr);
	}
	
	/**
	 * 测试方法
	 * @param args
	 */
	public static void main(String[] args) {
		ArrayBinaryTree binTree = new ArrayBinaryTree(4, "根结点");
		binTree.add(0, "第二层右子节点", false); // 第一个参数为需要添加子节点的父节点的索引： 即根节点
		binTree.add(2, "第三层右子节点", false);
		binTree.add(6, "第四层右子节点", false);
		System.out.println(binTree);
	}
}