算法设计与分析——斐波那契堆
引言
这章,我们来看看大名鼎鼎的斐波那契堆。这个堆就很有意思了,居然能和大名鼎鼎的斐波那契数列挂上边。
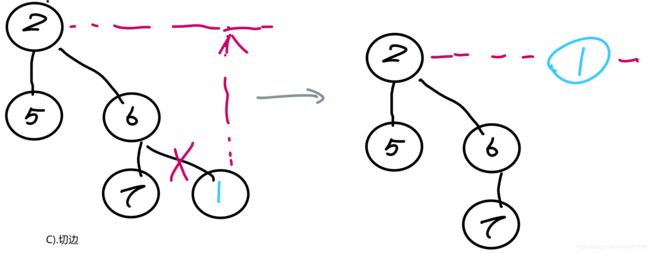
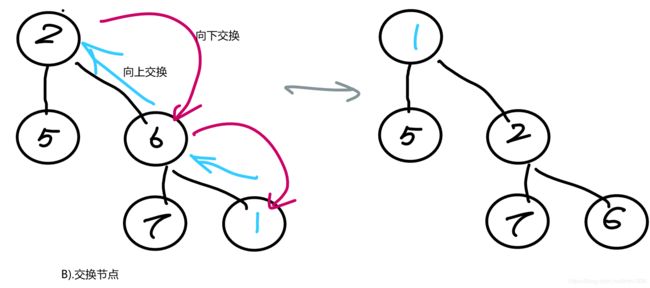
先回顾一下,上一篇博客 二项堆 有提到,在DECREASEKEY的时候,如果修改后的节点破坏了父节点的元素小于等于子节点元素的要求后,可以有两种策略:1.通过节点交换的方式,从下往上维护修改节点与父节点之间的堆序。这也是二项堆和二叉对的做法。2.把这个节点切下来,然后挂到根链上去。这种神奇的方法,就是斐波那契堆的做法。
下面举个例子来图示这两种过程。

把节点10改成1后。
基于交换的方式的示意图:
斐波那契堆
基于上面的例子,我们看到在修改值的时候基于交换的方式需要维护它与父节点以及祖先节点的堆序,而如果使用切边的方式 只要把这个边切下来挂到根链即可,看起来好像比交换快的多的多!但是如果不加限制的切边,那个切完以后剩下的树很可能会是一个很怪异的、与之前 B k B_{k} Bk树相差特别大的树,这样子是不好的。这么说好像有点空洞,为什么不好呢?
考虑这么一个情况,如果不加限制的切边,那么一个 B k B_{k} Bk可能会被切的支离破碎,那么这个树的节点数就没有下界了,对任意的 B k B_{k} Bk无脑切完以后 它剩下的节点数可能是 1 , 2 , 3 , 4 ⋅ ⋅ ⋅ 2 k 1,2,3,4···2^{k} 1,2,3,4⋅⋅⋅2k的。那么这个堆的可能存在的树的个数就有可能是n颗树,每棵树只有一两个节点,如果是这样的话 那么这个堆的性能会相当差。
因此,一定不可以无脑的切,必须要对这个切边加上一定的限制,使得每颗 B k B_{k} Bk树被切多次之后,剩下的节点树都有一个跟 k k k有关的下界。
斐波那契要求: B k B_{k} Bk树里面的任意节点最多只能被切掉一个孩子,如果这个孩子被切两次,那么把这个节点也从 B k B_{k} Bk树的根切下来挂到根链上。 在实现中,斐波那契堆通过给每个节点加上一个mask标记这个节点的孩子有没有被切掉过。
我们从实现的角度来一步步看看,斐波那契堆里面的细节。
斐波那契堆和二项堆其实是很相像的,斐波拉契堆其实就是放松条件下的二项堆。
定义节点
斐波那契堆各个节点的定义:
#include data_region用来存储数据;children用来保存这个节点所有孩子的指针,这是一个vector,是动态变化的。parent指向父节点,对于根节点来说,parent指向他自己。degree表示这个节点的孩子个数是多少。
mask显示以被节点的树被挂到根链前 到目前为止损失了多少孩子。
重点理解整个mask的含义。
定义fbHeap类
定义出fbHeap类,把要实现的成员函数先搬出来。
template <typename T>
class fbHeap
{
public:
fbHeap();
~fbHeap();
public:
void INSERT(T x);//插入数据x
void MAKEHEAP();//创建斐波那契堆
T FINDMIN();//找到最小值
T UNION(fbHeap & rhs);//与另外一个斐波那契堆合并
T EXTRACTMIN();//摘取最小值
void DECREASEKEY(_node <T> *ptr, T x);//将ptr节点的数据区改成x
void DELETE(_node <T> *ptr);//把ptr节点删除
private:
map<int, vector < _node<T> *> > FkHeads;
_node <T> * min;
};
我们的目标就是要实现好这些功能函数。
注意类里面有成员:map,这是一个int到数组的映射,FkHeads[k],就仿佛一个槽一样,里面放着那些挂在根链上度为k的树的根节点指针。FkHeads其实在这里就是起到了一个根链的作用,它把各个独立的树的根节点都关联起来。之所以 FkHeads[k]是个数组是因为在中间某个过程中,未合并前根链上可能存在多颗根的度为k的树。
之所以把FkHeaps定义为map是因为考虑到在两个斐波拉契堆合并的时候,一个堆比另外一个堆多了很多新的度的树。
_node< T> * min;指向整个堆最下的那个节点。
MAKEHEAP
MAKEHEAP建堆函数就是建立一个不含任何元素的斐波那契堆,这里的主要工作就是把BkHeads初始化一下,让它至少存在BkHeads[0]。即BkHeads现在可以接受度为0的树。
void MAKEHEAP()//创建斐波那契堆
{
min = NULL;
FkHeads.insert({ 0, {} });
}
INSERT(T x)
插入的时候就是新建一个度为0的节点,任何把这个节点插入到根链的度为0的槽中。
注意,当这个新节点插入后,FkHeads[0]可能存在两个度为0的树,此时斐波拉契堆先不忙着合并,而是等待一个合适的时机再统一合并起来。
void INSERT(T x)//插入数据x
{
_node<T> n = new _node<T>();
n->data_region = x;
n->parent = n;
n->degree = 0;
n->mask = 0;
if (x < min->data_region)
//新插入一个更小的值
{
min = n;
}
FkHeads[0].push_back(n);//将这个新插入的节点作为度为0的树插入到FkHeads[0]
}
FINDMIN
这个没什么好说的,min维护着最小的节点的值,那么直接返回min的值就是了。
T FINDMIN()//找到最小值
{
if (min != NULL)
{
return min->children;
}
printf("Error\n");
return T();//异常
}
注意min是指向堆里面最小的节点的指针,那么min的更新时机为:
- 插入新的值,如果插入一个比当前最小值还要小的值,那么修改min。
- 删除最小的值,此时min指向的对象要被改了,那么min当然要另寻它主了。
- 修改某个节点的值,如果修改后的值比堆的最小值还要小,那么min就要修改。
UNION(fbHeap & rhs)
把另外斐波那契堆合并到本身的这个堆里面来。
合并的方式也是很简单粗暴,就是把rhs的FkHeads和本身的FkHeads合并起来,然后更新min。
注意,这么也没有对合并后的FkHeads进行合并。
如果根链不使用map来实现,让所有的根链通过双向链表来连接也是可以的。
T UNION(fbHeap & rhs)//与另外一个斐波那契堆合并
{
map<int, vector<_node<T> *> >::iterate it;
for (it = rhs.FkHeads.begin(); it != rhs.FkHeads.end(); it++)
{
int degree = it->first;
vector<_node<T> *> tree = it->second;
if (this->FkHeads.find(degree) == this->FkHeads.end())
//本堆的根链上不存在一个度为degree的树
{
this->FkHeads.insert({ degree, {} });
}
for (int i = 0; tree.size(); i++)
{
this->FkHeads[degree].push_back(tree[i]);
}
}
}
接下来就要设计EXTRACMIN了。
EXTRACTMIN
到了这个函数就是要进行合并了哇。
先得到最小值,然后把这个最小的孩子都挂在根链上,再把min从根链中删除。最后调用maintain()函数维护FkHeads根链里面 相同度的树合并成新的度增加的树。
T EXTRACTMIN()//摘取最小值
{
T rst = min->children;
//把它所有的孩子都挂到根链上
for (int i = 0; i < min->children.size(); i++)
{
FkHeads[min->children[i]->degree].push_back(min->children[i]);
}
//摘除min
vector<_node<T> *> ::iterate it = FkHeads[min->degree].begin();
for (; it != FkHeads[min->degree].end(); it++)
{
if (it->parent == min)
{
break;
}
}
if (it != FkHeads[min->degree].end())
{
FkHeads[min->degree].erase(it);
}
//维护FkHeads把相同的度的树合并
maintain();
return rst;
}
OK,现在看看maintain函数是怎么实现的。
maintain()
maintain函数的核心步骤:
1.遍历根链FkHeads上所有的可能度的树
2.把相同度的树合并成度加1的树
3.更新min指针,这是因为maintain只EXTACTMIN中被调用,而每一次EXTRACTMIN都需要更新min指针,因为它需要就得最小值删除。
void maintain()
//维护FkHeads函数,使得度为k的树最多只有一颗
{
min = NULL;
for (auto it = FkHeads.begin(); it != FkHeads.end(); it++)
{
int degree = it->first;
while (true)
{
if (FkHeads[degree].size() > 1)
//说明有不止一颗度为degree的树,将它们两两合并
{
_node <T>* f = FkHeads[degree][FkHeads[degree].size() - 1];
FkHeads[degree].pop();
_node <T>* s = FkHeads[degree][FkHeads[degree].size() - 1];
FkHeads[degree].pop();
//合并
if(f->data_region > s->data_region)
{
_node<T>* tmp = f;
f = s;
s = tmp;
}
f->degree++;
s->parent = f;
f->children.push_back(s);
if (FkHeads.find(f->degree) == FkHeads.end())
{
FkHeads.insert({ f->degree, {} });
}
FkHeads[f->degree].push_back(f);
if (min == NULL)
{
min = f;
}
else if (min->data_region > f->data_region)
{
min = f;
}
}
else if (FkHeads[degree].size()==1)
//已经处理到最多只剩下一个了
{
if (min == NULL)
{
min = FkHeads[degree][0];
}
else if (min->data_region > FkHeads[degree][0]->data_region)
{
min = FkHeads[degree][0];
}
break;
}
}
}
}