多分类问题的性能评价指标 f1-score

本文主要从二分类开始说起，介绍多分类问题的性能评价指标 f1-score

首先，先给出二分类问题$f1-score$的计算公式，
$$f1-score=\frac{1}{\frac{1}{2}(\frac{1}{P}+\frac{1}{R})}=\frac{2PR}{P+R}$$ $$P=\frac{TP}{TP+FP}$$ $$R=\frac{TP}{TP+FN}$$

其中$P$叫做查准率precision，$R$叫做查全率recall。

分类结果的混淆矩阵如下，

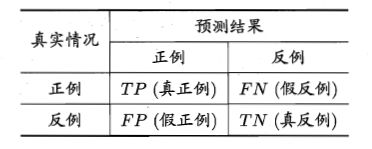
对于$TP,TN,FP,FN$怎么去理解呢？$T$或者$F$表示分类器是分对了还是分错了，分对了就是$T$，分错了就是$F$；$P$或者$N$表示分类器把该样本分成了什么，分成了正例就是$P$，分成了负例就是$N$。以$FP$为例，表示分类器把该样本分错了，并且把它分成了正例。

那么$P$和$R$怎么理解呢？以好坏瓜的分类为例，$P$表示被分类器分成好瓜的样本中确实是好瓜的比例；$R$表示所有的好瓜中被分类器分成是好瓜的比例。

所以，如果$P$很高，$R$很小，说明分类器太过谨慎，只把有很大把握认为是好瓜的样本才确认为是好瓜；反之，如果$P$很小，$R$很高，说明分类器就是"宁愿错杀三千，也不漏过一个"。这两种情况显然都不是一个好的分类器。

所以我们希望能够有一个$P$和$R$都比较高的分类器，那么我们怎样通过$P$和$R$来量化分类器的性能呢？类似于ROC-AUC，可以使用P-R曲线下面积来表示分类器的性能。面积越大的表示分类器性能越好，但是一般这个面积不太好求，所以引入了开头提到的$f1-score$的概念，$f1-score$越接近1，分类器性能越好。

上述是对于二分类问题$f1-score$的求法，那么对于多分类问题呢？一般多分类的问题的处理方法是"ovo"或者"ovr"，分别会存在$\frac{n(n-1)}{2}$或者$n$个混淆矩阵，那么我们如何在$m$个混淆矩阵上求$f1-score$呢？

有两种作法，分别是$macro-F1$以及$micro-F1$

macro-F1

对各个$P_i$和$R_i$求平均，再求$F1$

$$macro-P=\frac{1}{m}{\Sigma }_i{P}_i$$ $$macro-R=\frac{1}{m}{\Sigma }_i{R}_i$$ $$macro-F1=\frac{2\ast macro-P\ast macro-R}{macro-P+macro-R}$$

micro-F1

对各个$TP,TN,FP,FN$求平均，再求$P,R,F1$

$$micro-P=\frac{\overline{TP}}{\overline{TP}+\overline{FP}}$$ $$micro-R=\frac{\overline{TP}}{\overline{TP}+\overline{FN}}$$ $$micro-F1=\frac{2\ast micro-P\ast micro-R}{micro-P+micro-R}$$

$macro-F1$以及$micro-F1$也是越接近1越好。

sklearn接口

在 sklearn 中也提供了计算$f1-score$的接口，官网给出的实例如下，

>>> from sklearn.metrics import f1_score
>>> y_true = [0, 1, 2, 0, 1, 2]
>>> y_pred = [0, 2, 1, 0, 0, 1]
>>> f1_score(y_true, y_pred, average='macro')
0.26...
>>> f1_score(y_true, y_pred, average='micro')
0.33...

可见上述接口求$micro-F1$和$macro-F1$的时候，都是建立了n个混淆矩阵，每个混淆矩阵是把一个类当作正例，其他的类当负例求出$TP,TN,FP,FN$的值，再按照之前介绍的方法，求出$F1$的值。

参考资料：
《机器学习》周志华
https://scikit-learn.org/stable/modules/generated/sklearn.metrics.f1_score.html#sklearn.metrics.f1_score