冈萨雷斯《数字图像处理》学习笔记（5）--图像分割

一、点、线和边缘检测

这里用的图像检测方法主要是滤波操作。模板在图像中任意一点的响应R由下式给出：

R=∑i=19ωizi R = ∑ i = 1 9 ω i z i

其中， zi z i 是与模板系数 ωi ω i 相关的像素的灰度。
下面是点检测的模板：

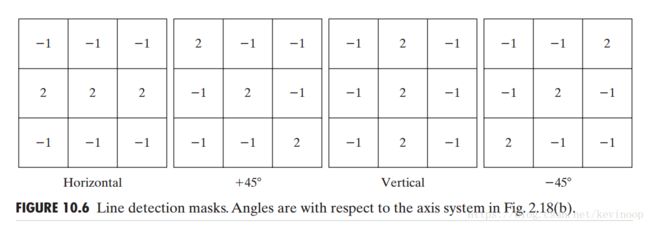
线检测的模板如下（分别检测水平，45度，垂直和-45度的线）：

在谈边缘检测前，先看些基础知识：
二维函数的梯度定义如下：

▽f=⎡⎣∂f∂x∂f∂y⎤⎦ ▽ f = [ ∂ f ∂ x ∂ f ∂ y ]

幅值定义为： mag(▽f)=[(∂f∂x)2+(∂f∂y)2]12 m a g ( ▽ f ) = [ ( ∂ f ∂ x ) 2 + ( ∂ f ∂ y ) 2 ] 1 2
可以用下列两种方式近似：
mag(▽f)≈(∂f∂x)2+(∂f∂y)2 m a g ( ▽ f ) ≈ ( ∂ f ∂ x ) 2 + ( ∂ f ∂ y ) 2
mag(▽f)≈|∂f∂x|+|∂f∂y| m a g ( ▽ f ) ≈ | ∂ f ∂ x | + | ∂ f ∂ y |
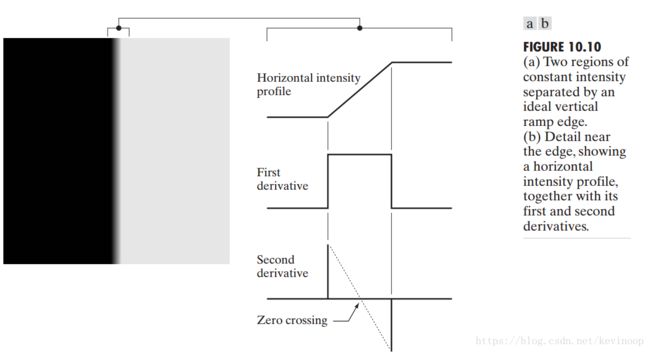
边缘检测使用如下两个准则之一来找到图像中灰度快速变化的位置：

1. 寻找灰度的一阶导数的幅度大于某个指定的阈值。
2. 寻找灰度的二阶导数有零交叉的位置。

我们可以从下面的图看出为什么要使用上面两个准则。

很明显一阶导数幅度大的地方表示图像灰度变化十分剧烈，同理二阶导数的零交叉点也是灰度变化十分剧烈的位置。

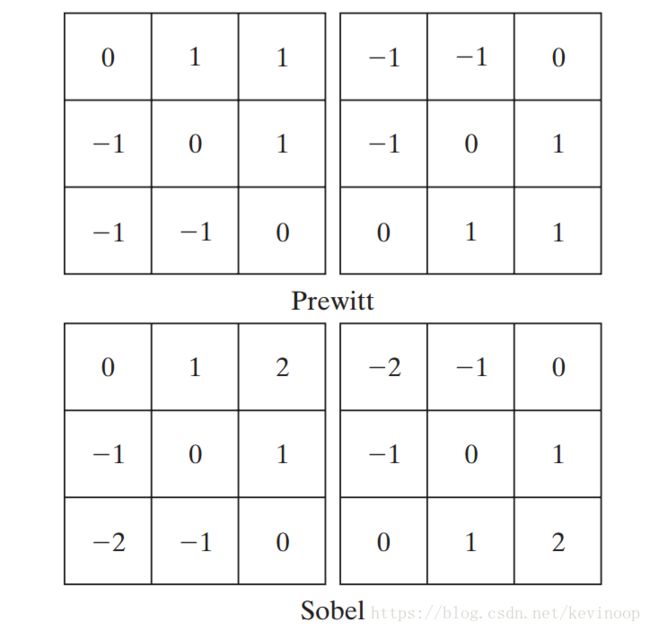
又根据导数在数值上可近似为差分。我们利用如下滤波器可以达到边缘检测的目的。

LoG检测器
考虑高斯函数：

G(x,y)=ex2+y22σ2 G ( x , y ) = e x 2 + y 2 2 σ 2

该函数的拉普拉斯算子是（即二阶微分）：

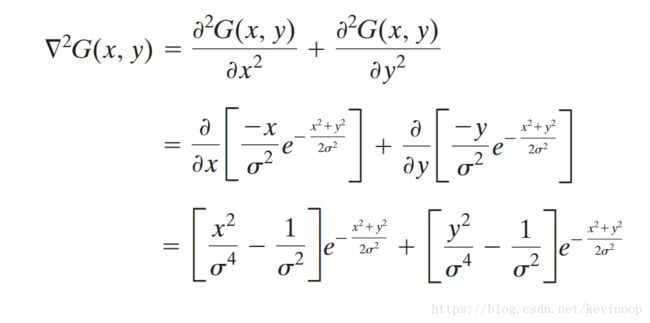
使用它卷积的效果： 平滑图像，降低噪声，产生一幅双边缘图像。因此可以通过双边缘之间的零交叉来定位边缘。

二、霍夫变换

采用Hough变换时，我们考虑一个点 (xi,yi) ( x i , y i ) 和所有通过该点的直线。很明显，有无数条经过点 (xi,yi) ( x i , y i ) 的直线，这些线对某些a值和b值来说，均满足 yi=axi+b y i = a x i + b 。将该公式写为 b=−axi+yi b = − a x i + y i 并考虑ab平面(也称为参数空间)，可对一个固定点 (xi,yi) ( x i , y i ) 产生单独的一条直线。此外，第二个点 (xj,yj) ( x j , y j ) 也有这样一条在参数空间上与它相关的直线，这条直线和与 (xi,yi) ( x i , y i ) 相关的直线相交于点 (a′,b′) ( a ′ , b ′ ) ，其中a’和b’分别是xy平面上包含点 (xi,yi) ( x i , y i ) 和 (xj,yj) ( x j , y j ) 的直线的斜率和截距。事实上，在这条直线上的所有点都有在参数空间中相交于点 (a′,b′) ( a ′ , b ′ ) 的直线。下图说明了这些概念。

但这种方法在直线趋近于垂直时，a 的值将趋于无穷大。因此我们用法线来表示直线：

xcosθ+ysinθ=ρ x c o s θ + y s i n θ = ρ

下图（a）说明了 ρ ρ 和 θ θ 的几何意义。图（b）中每一条曲线表示通过 (xi,yi) ( x i , y i ) 的一族直线。图（c）是将参数空间离散化进行计算。

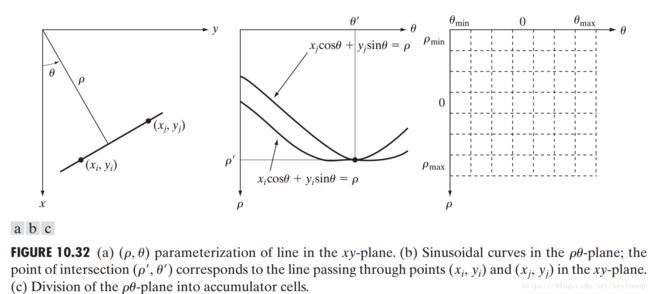
霍夫变换把参数空间细分为 累加器单元。其中， −D⩽ρ⩽D − D ⩽ ρ ⩽ D （D是图像中两个对角之间的最远距离）。 −90度⩽θ⩽90度 − 90 度 ⩽ θ ⩽ 90 度 。最初每一个累加器单元数值设置为0。然后对图像中的每一个点 (xk,yk) ( x k , y k ) ，使用所有离散化后的 θ θ 值代入公式 ρ=xkcosθ+yksinθ ρ = x k c o s θ + y k s i n θ 求出相应的 ρ ρ 值（将 ρ ρ 值四舍五入为沿 ρ ρ 轴最接近的允许单元值 ）。同时相应的累加器单元加1。上面的过程结束后，累加器表上记录下来的每个单元 (i,j) 的数值Q就意味着在xy平面上有Q个点位于线 xcosθj+ysinθj=ρi x c o s θ j + y s i n θ j = ρ i 上。该表中最大的所对应的 (ρ0,θ0) ( ρ 0 , θ 0 ) 就是xy平面上共线点数数目最多的直线方程的参数。

三、阈值处理

全局阈值处理

使用 Otsu 方法进行最佳全局阈值处理

类间方差最大化的思想是方差越大，越接近正确分割图像的阈值。下面给出类间方差的表达式（假设选定一个阈值k，C1是灰度级为[0,1,2,3,…,k]的一组像素，C2是灰度级为[k+1,..,.L-1]的一组像素）：

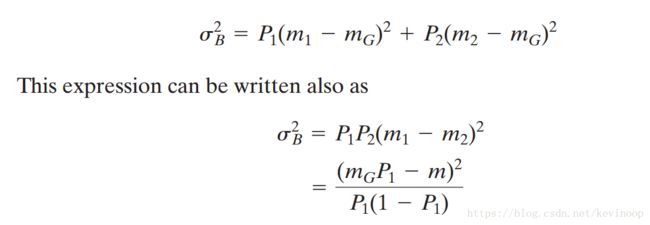
其中， p1(k) p 1 ( k ) 是集合C1发生的概率， p2(k) p 2 ( k ) 是集合C2发生的概率：
P1(k)=∑ki=0pi P 1 ( k ) = ∑ i = 0 k p i
P2(k)=∑L−1i=k+1pi P 2 ( k ) = ∑ i = k + 1 L − 1 p i

m1(k) m 1 ( k ) 是集合C1像素的平均灰度， m2(k) m 2 ( k ) 是集合C2像素的平均灰度， mG m G 是全局均值：
m1(k)=∑ki=0ipi m 1 ( k ) = ∑ i = 0 k i p i
m2(k)=∑L−1i=k+1ipi m 2 ( k ) = ∑ i = k + 1 L − 1 i p i
mG(k)=∑L−1i=0ipi m G ( k ) = ∑ i = 0 L − 1 i p i

定义类间方差与图像总灰度方差的比值为： η(k)=σ2B(k)σ2G η ( k ) = σ B 2 ( k ) σ G 2

使用移动平均值的图像阈值处理

令 zk+1 z k + 1 表示第 k+1 步扫描时所遇到的点的灰度，那么这个新点处的移动平均由下式给出：

m(k+1)=m(k)+1n(zk+1−zn−k) m ( k + 1 ) = m ( k ) + 1 n ( z k + 1 − z n − k )

使用下式实现分割：

f(x,y)={1,f(x,y)>Kmx,y0, other situation f ( x , y ) = { 1 , f ( x , y ) > K m x , y 0 ,   o t h e r   s i t u a t i o n

其中K是[0,1]区间的常数， mxy m x y 是输入图像中点（x,y）处的移动平均。

四、分水岭图像分割

构建大坝（Dam Construction）

最简单的构建大坝的方法就是利用形态学运算——膨胀。
下图展示了第n-1步淹没的两个集水盆地：

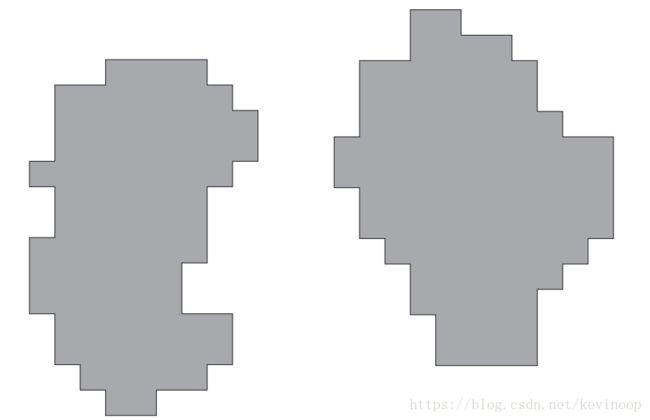
接着展现了第 n 步淹没的结果：

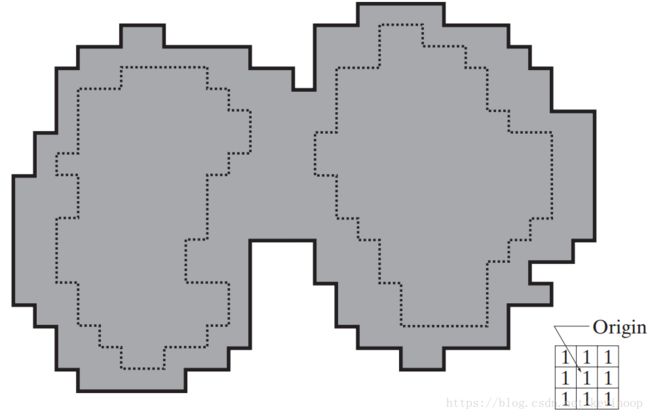
最后构建水坝：

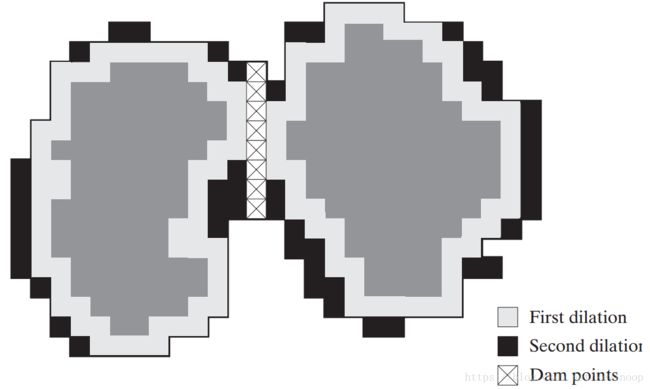
为了说明下文，令M1和M2表示两个区域中的最小值点坐标的集合。将集水盆地点的坐标集合与这两个在溢出的第n-1步的最小值点的坐标集合联系起来，在第n-1步溢出处，两个最小值分别表示为 Cn−1(M1) C n − 1 ( M 1 ) 和 Cn−1(M2) C n − 1 ( M 2 ) 。它们代表上图第一幅图的两个灰色区域。再令C[n-1]表示这两个集合的并集。上图第一幅图有两个连通分量，第二幅图只有一个连通分量。令q表示第二幅图的连通分量。注意到，第一幅图的两个连通分量可以由“与”操作（ q∩C[n−1] q ∩ C [ n − 1 ] ）从q中提取出来。

分水岭算法

令 M1 M 1 , M2 M 2 … … 表示图像g(x,y)的区域最小值的坐标的集合， C(Mi) C ( M i ) 表示与区域最小值 Mi M i 联系的集水盆地的点的坐标集合。令 Cn(Mi) C n ( M i ) 表示集水盆地与淹没阶段n的区域最小值 Mi M i 联系的的点的坐标集合，最后令T[n] 表示满足 g(s,t)<n g ( s , t ) < n 的坐标(s,t) 的集合。根据上面的理解，可看出 Cn(Mi) C n ( M i ) 是由下式给出的一幅二值图像：

Cn(Mi)=C(Mi)∩T[n] C n ( M i ) = C ( M i ) ∩ T [ n ]

接下来，我们令C[n]表示在阶段n 中已被水淹没的集水盆地的并：

C[n]=∪Ri=1C(Mi) C [ n ] = ∪ i = 1 R C ( M i )

我们可以理解为：C[n-1]中的每一个连通分量都恰好包含在T[n]的一个连通分量。下面是分水岭算法的步骤：