LeetCode 题解 | 198.打家劫舍

LeetCode 题解 | 198.打家劫舍 

198.打家劫舍

打家劫舍 - 力扣（LeetCode）​leetcode-cn.com

题目描述

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你在 不触动警报装置的情况下，能够偷窃到的最高金额。

示例 1:

输入: [1,2,3,1]
输出: 4
解释: 偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
        偷窃到的最高金额 = 1 + 3 = 4 。

示例 2:

输入: [2,7,9,3,1]
输出: 12
解释: 偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
        偷窃到的最高金额 = 2 + 9 + 1 = 12 。

 

解决方案

根据这道题的条件特点：

如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警（即相邻的数字不能同时作为最终求和的有效数字）。

 

分析

这个条件如果精简掉其他内容，很容易让人联想到奇偶数。这个解法就是从这点出发。

• 设置两个变量，sumOdd 和 sumEven 分别对数组的奇数和偶数元素求和。
• 最后比较这两个和谁更大，谁就是最优解。

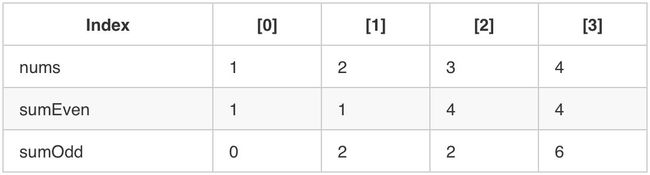
至少在下面这个例子里，这么做是成功的了。

接下来要解决的就是最优解不是纯奇数和或者偶数和的情况。

这种情况下，最优解可能前半段出现在这边，后半段出现在另一边。那么只要找到一个时机，当这一段的最优解没有另一边好时，就复制对面的最优解过来。

 

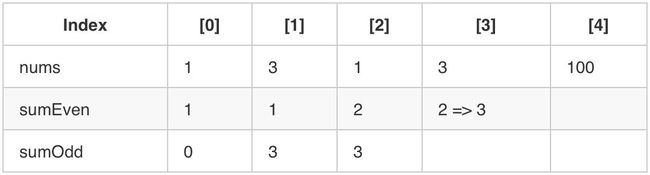
举个例子：

当偶数和（奇偶指的数组下标）加到第二个 1 之后，发现还不如奇数和一个 3 大，就应该将对面的3复制过来替换掉自己的 2。

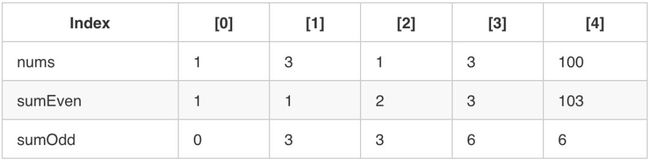
继续计算后得到最优解。

 

思路

1. 设置两个变量，sumOdd 和 sumEven 分别对数组的奇数和偶数元素求和。
2. 遍历数组，索引为奇数时，将元素加到奇数和，并与偶数和比较更新成max。
3. 偶数和同理。
4. 返回时进行最后一次更新max。

 

​C++ 实现

int rob(vector& nums) 
{
	int sumOdd = 0;
	int sumEven = 0;

	for (int i = 0; i < nums.size(); i++)
	{
		if (i % 2 == 0)
		{
			sumEven += nums[i];
			sumEven = max(sumOdd, sumEven);
		}
		else
		{
			sumOdd += nums[i];
			sumOdd = max(sumOdd, sumEven);
		}
	}
	return max(sumOdd, sumEven);
}