最长上升子序列 nlogn (导弹拦截)
先给出模板题目链接
拦截导弹
遇到最长不下降子序列, 我们第一时间想到的是O(n^2)的算法, 该算法简便易懂而且代码也好写, 不像nlogn这个, 代码几分钟,边界问题调试了我几十分钟......
先来讲理解思路
对于n(log n)这个解法, 除了一个保存数据的数组之外,还需要一个额外的数组(前者在一定情况下省略,也就是说边输入边进行运算).
定义另一个数组为 tmp[maxn](数组始终有序,具体为什么请往下面看)
除此之外需要一个p=1用来表示最长上升序列的个数
下面用图形表示代码运行过程
序列: 1 3 2 4 5
初始我们的tmp数组是这样的
在3到的时候发现3比P[1]大,于是将3放到1的后面,此时上升序列有两个.
数组变成了这个样子
然后后面又来了一个2, 这个时候发现3比2要大, 这个时候我们用二分查找去找2可以更改的位置
发现2可以放在p[1]后面, 于是把p[2]更新为2.( 为什么更新以及更新的作用我会在后面解释, 请耐心往下看 ).
接下来的数组是这个样子的
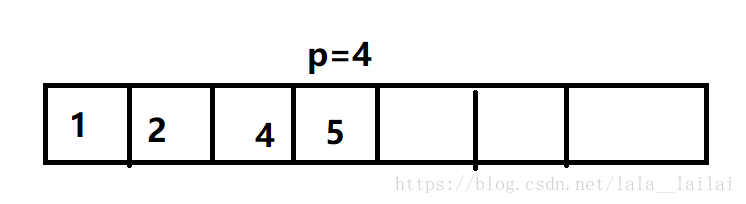
后面紧跟序列4 5, 是一个递增的序列, 4比P[2]大,所以4放到P[2]后面, p[3] = 4, 然后 5比p[3]大, p[4] = 5, 数组是这个样子的
为了解释之前为什么用2去更改3,我们在给定的序列1 3 2 4 5 后面加几个数, 2 2 2,
这样的话标准的不上升序列是1 2 2 2 2.然而到5为止,我们求到的序列是1 2 4 5.
后面继续用该算法去求
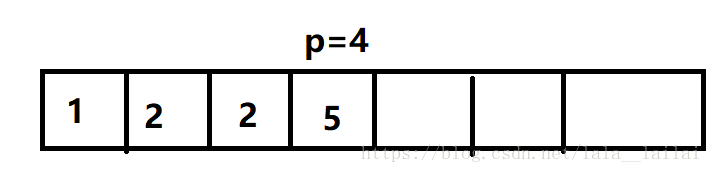
进来一个2,发现2比P[4]=5要小,于是找到他能插入的最大的位置,于是找到了p[3]=4, 将p[3]置为2,该数列变成
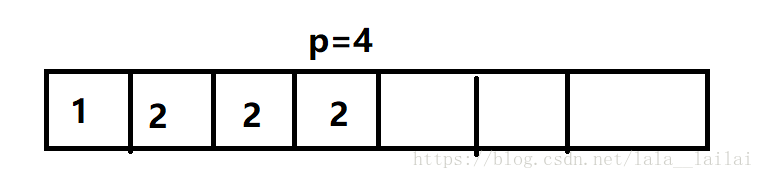
然后又进来一个2, 发现p[4]还是要大于2, 所以继续寻找可以插入的位置, 然后把p[5]更新成2.
于是数列变成
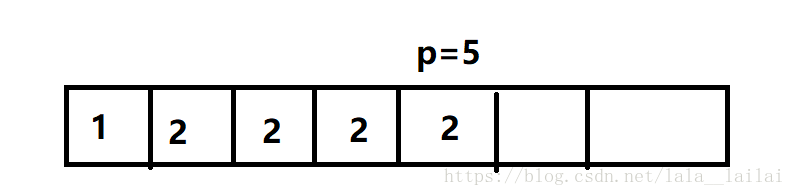
然后进来一个2,插入到最后序列就变成了
结果√
最后总结一句, 因为是最长不下降子序列, 我们需要考虑的只有最后选择的一个数,
前面已经选择的数的更改是不会影响到最终的长度的,反而如果前面的数一直更改到了最后一个
说明这里用一个更小的数将最后一个数给替代了, 因为对于后面我们不知道的序列, 为了达到最长, 我们当前选择的这个数当然越小越好.
(...说不清楚了不说了...)
下面贴出导弹拦截nlogn代码
解题方法: 先求一边最长不上升子序列,再求一边最长上升子序列
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int maxn = 100005;
int sz[maxn],tp[maxn]; //
int n=1;
int p=1;
int main(){
while(cin>>sz[n]) n++;
tp[1] = sz[1];
for(int i=2;i>1;
while(l!=r){
if(sz[i] > tp[mid]) r = mid;
else l = mid+1;
mid = (l+r)>>1;
}
tp[l] = sz[i];
}
}
cout< tp[p]) tp[++p] = sz[i];
else{
int l=1,r=p,mid=p>>1;
while(l!=r){
if(sz[i] <= tp[mid] ) r = mid;
else l = mid+1;
mid = (l+r)>>1;
}
tp[l] = sz[i];
}
}
cout<