模式识别经典算法——Kmeans图像聚类分割(以最短的matlab程序实现)
kmeans之于模式识别,如同“hello world”之于C、之于任何一门高级语言。
算法的规格(specification)
在聚类问题(一般非监督问题)中,给定训练样本 X={x(1),x(2),…,x(N)} ,每个 x(i)∈Rd 。kmeans算法的职责在于将这 N 个样本聚类成 k 个簇(cluster, μ1,μ2,…,μk ),流程如下:
随机选取 k 个聚类中心(cluster centroids)为 μ1,μ2,…,μk
C = X(randperm(m*n, k), :); # 程序语言重复一下过程直至收敛
{
对于每一个样本 i ,根据最近邻(欧氏距离度量)计算其所属分类
c(i):=argminj∥x(i)−μj∥2
对于每一个类 j ,重新计算该类的质心(centroids)
μj:=∑mi=11{c(i)=j}x(i)∑mi=11{c(i)=j}
}
算法的规格:
- 一个参数 k ,聚类中心的数目,当然也有一些常规的参数,比如最大迭代次数 epochs ,容忍度 tol
- 一个循环,判断目标函数是否变化足够小,以 F 范数(Frobenius norm)为度归。
while true,
...
if norm(J_cur-J_prev, 'fro') < tol,
break;
end
J_prev = J_cur;
end- 一条更新语句,更新各个类的聚类中心,根据每个样本应属的类别(欧式距离最小表征)
μj:=∑mi=11{c(i)=j}x(i)∑mi=11{c(i)=j}
这个公式看似高大上,实则不值一提,翻译过来就是新的聚类中心(centroid)在该类别空间的中心处。
dist = sum(X.^2, 2)*ones(1, k) + (sum(C.^2, 2)*ones(1, m*n))'...
- 2*X*C';
[~, idx] = min(dist, [], 2) ;
for i = 1:k,
C(i, :) = mean(X(idx == i , :)); # 对应于这样一条语句
endmatlab实现
客户端(client)程序
clear all; close all;
I = imread('./lena.bmp');
[m, n, p] = size(I);
k = 7;
[C, label, J] = kmeans(I, k);
I_seg = reshape(C(label, :), m, n, p);
figure
subplot(1, 2, 1), imshow(I, []), title('原图')
subplot(1, 2, 2), imshow(uint8(I_seg), []), title('聚类图')
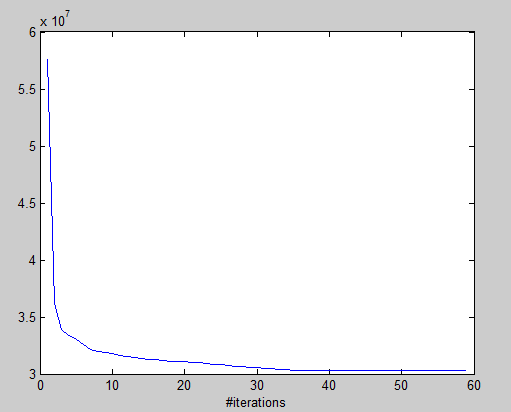
figure
plot(1:length(J), J), xlabel('#iterations')kmeans函数
function [C, label, J] = kmeans(I, k)
[m, n, p] = size(I);
X = reshape(double(I), m*n, p);
rng('default');
C = X(randperm(m*n, k), :);
J_prev = inf; iter = 0; J = []; tol = 1e-2;
while true,
iter = iter + 1;
dist = sum(X.^2, 2)*ones(1, k) + (sum(C.^2, 2)*ones(1, m*n))' - 2*X*C';
[~, label] = min(dist, [], 2) ;
for i = 1:k,
C(i, :) = mean(X(label == i , :));
end
J_cur = sum(sum((X - C(label, :)).^2, 2));
J = [J, J_cur];
display(sprintf('#iteration: %03d, objective fcn: %f', iter, J_cur));
if norm(J_cur-J_prev, 'fro') < tol,
break;
end
J_prev = J_cur;
end
实验结果
目标函数收敛情况
目标函数
J(c,μ)=∑i=1m∥x(i)−μc(i)∥2
matlab计算程序:
J_cur = sum(sum((X - C(label, :)).^2, 2));