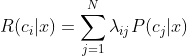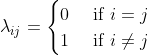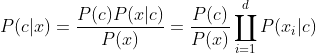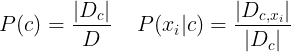机器学习专题（二）—— 朴素贝叶斯算法的python实现

大家好，沉寂了好久之后，终于决定发第二篇文章。闲话少叙，请看正文。
朴素贝叶斯是贝叶斯决策论的一部分，在讲述贝叶斯之前，先阐述一下贝叶斯决策论。
一、贝叶斯决策论
贝叶斯决策论是概率框架下实施决策的基本方法。我们以多分类任务为例来解释其基本原理
1.1贝叶斯条件风险的提出：假设有N种可能的类别标记，即,表示将一个真实标记为的样本误分为所产生的损失。那么基于后验概率P(|),我们可以将样本x分类为所产生的期望损失表示为：

上式也成为样本x上的“条件风险”。

---

那么贝叶斯分类的目标就是：找到一个判定准则h(.),使得R(h)的总体风险最小，也就是期望损失最小。显然，对于每个样本想，如果h能够最小化条件风险R(h(x)|x),则总体风险R(h)也将被最小化。这样我们就得到了贝叶斯判定准则，即：

为最小化总体风险，只需在每个样本x上选择能使条件风险R(c|x)最小的类别标记即可:

称为“贝叶斯最优分类器”。

---

那么如果我们假定
则由于

故问题可转化为求解P(c|x)的最大值，即

即对每个样本x,选择能使P(c|x)最大的类别标记之。

1.2 贝叶斯后验概率的计算：

接着上面的内容，我们知道，朴素贝叶斯决策的关键变为计算后验概率P(c|x)的值。估算P(c|x)通常有两种方法：
1）判别式模型：即通过直接建模P(C|X)来预测C;
2）生成式模型：即通过计算P(x,c)的联合分布，推出P(c|x)的值

决策树、BP神经网络、支持向量机等都属于“判别式模型”。这里我们采用“生成式模型”.
基于“贝叶斯定理”，我们知道：

P(c|x) = P(x,c)/P(x) = P(c)P(x|c) / P(x)

其中P(x)是用于归一化的“证据因子”，与类别标记无关。因此计算P(C|X)的问题转化为计算 P(C)P(X|C)。P(C)的计算通过频率估计即可获得，因此最终问题确定在了计算 P(X|C)上。
由此我们提出了“朴素贝叶斯分类器”

---

二、朴素贝叶斯分类器

由上面的讨论我们知道，计算类后验概率P(C|X)的难度主要在于计算类条件概率P(X|C).P(X|C)为样本所有属性的联合概率，如果假设样本的“所有属性是相互独立的“,则有：

其中为x在第i个属性上的取值，d为属性的个数。由于P(X)不影响类标记，所以我们得出了“朴素贝叶斯分类”的判定准则为：

（敲黑板。。。这才是本文的重点）
需要注意的是：朴素贝叶斯分类是建立在“假设样本属性相互独立”的条件之上，其中

为数据集D中第c类样本的集合，为中第i个属性为的样本的集合。
当然，如果样本的属性值为连续值，则的计算可通过概率函数来获得。假定，即属性值服从高斯分布，则有：

其中和为第c类样本在第ｉ个属性值上的“均值”和“方差”。

附加内容：
分析朴素贝叶斯分类的判定准则 ，我们发现：如果某个属性的类条件概率的值为0，那么真个公式的值将会变为0，这显然是不符合实际情况的。为了避免这种“尴尬”，我们引出了“平滑”的概念（又称拉普拉斯修正）。
具体地，拉普拉斯修正是指：令N表示训练集中可能包含的样本类别总数，表示第i个属性可能的取值数，则我们可以将P(c)和P(x|c)的计算修正为：

这样我们就会避免0乘以任何数得0的问题。
至此，朴素贝叶斯分类器的基本原理我们已经基本掌握在手。接下来我将要展示的是一个“朴素贝叶斯分类器”的python实现样例。

---

三、朴素贝叶斯分类的Python实现
本文Python代码来源于《机器学习实战》一书，源代码我添加了大量的注释，方便大家理解。我们先从介绍问题开始讲起。
本文的python实现是一个使用朴素贝叶斯对文档进行分类的简单示例。

3.1、加载数据集
那么首先我们需要的是一些文本数据，因此第一步为加载数据集：

"""
使用Bayes分类器对文本进行分类
"""
from numpy import *
# 从文本中构建词向量，词表到向量的转换函数
def loadDataSet():
    """
    创建一些实验样本
    :return:
    """
    # 进行词条切分后的文档集合,每一行向量代表一个文档
    postingList =[['my','dog','has','flea','problems ','help','please'],
                  ['maybe','not','take','him','to','dog','park','stupid'],
                  ['my','dalmation','is','so','cute','I','love','him'],
                  ['stop','posting','stupid','worthless','garbage'],
                  ['mr','licks','ate','my','steak','how','to','stop','him'],
                  ['quit','buying','worthless','dog','food','stupid']]
    # 类别标签集合，表示文档是否为侮辱性文档
    classVec = [0,1,0,1,0,1]    # 1代表侮辱性文字  0代表正常言论
    return postingList,classVec

注：这里loadDataSet()函数创建了一些实验样本，该函数返回的第一个变量是已经进行了词条切分的文档集合postingList，这里文档数组一共有6行，表示有6个文档。第二个返回变量classVec则是6个文档的分类类型，1表示该文档含有侮辱性文字，0表示该文档为正常言论。

3.2、获取文档的词向量
在加载完文档数据集后，我们应该怎么使用这些文档呢？首先我们想到的是应该将这些文档转换为我们可以计算利用的变量。为此我们需要将一篇文档用“词向量”来表示，如何表示呢？
有一种方式就是先创建一个包含所有文档词汇的词列表集合，该集合中每个元素只出现一次。假设我们有一个含有10个单词的词列表集合，表示为 Dictionary = {x_1,x_2,……x_10}，那么对于某篇文档y(该文档中包含的单词数量一定少于或者等于10)，我们可以将其表示为一个长度为10的文本向量。向量的元素y[i]取值为：

y[i] = 0 ，如果Dictionary中第i个位置的单词没有出现在该文档
y[i] = 1 ，如果Dictionary中第i个位置的单词在该文档y中出现

所以通过这种方式，我们就可以将一篇文档用长度与词列表大小相同的向量来表示。下面createVocabList()函数就是创建一个不包含重复词汇的词列表。

def createVocabList(dataSet):
    """建一个包含所有文档中出现的不重复词的列表
    创
    :param dataSet:
    :return:
    """
    vocabSet = set([])      # 创建一个空集 set()函数返回一个无序不重复元素的集合
    for document in dataSet:
        vocabSet = vocabSet | set(document)     # 创建两个集合的并集
    return list(vocabSet)

在创建为词汇列表之后，紧接着就是文档的向量化表示了，具体方式上面已经提到，这里直接贴代码

def setOfWords2Vec(vocabList,inputSet):
    """
    使用“词集模型”
    :param vocabList: 词汇表
    :param inputSet:  单个的文档
    :return:  returnVec 词汇向量
    """
    returnVec = [0]*len(vocabList)  # 创建一个和词汇表等长的0向量，用来表示词汇表中的单词在文档中是否出现
    # 对于文档中单词，如果在词汇表中存在，则将词汇向量的对应位置设为1，否则设为0
    for word in inputSet:
        if word in vocabList:
            returnVec[vocabList.index(word)] =1     # index() 函数用于从列表中找出某个值第一个匹配项的索引位置。
        else:
            print("the word:%s is not in my Vocabulary!" % word)
    return returnVec

注：setOfWords2Vec()函数的作用就是将某个文档y向量化。

3.3 训练算法：朴素贝叶斯算法的类条件概率的计算

在处理完所有的文档数据之后，接下来就需要计算贝叶斯算法用到的各种概率了。我们以完成数据处理的文档作为数据集。在已经知道一个词是否出现在一篇文档中，以及该文档所属的类别之后。我们就可以计算概率了。根据“朴素贝叶斯判定准则”：
1）计算P(C):
显然，P(C)的计算非常容易，我们只需要用类别i中的文档数除以总的文档数就可以了。这里一共有两种分类（侮辱性文档和非侮辱性文档）。
2）计算P(X|C):

================
未更完