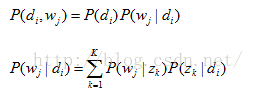LDA算法调研报告

LDA算法调研报告

 

1、LDA算法概述

    本文所阐述的LDA算法全称为Latent Dirichlet Allocation（网上没有标准的中文名称，我称之为潜在狄利克雷分配算法），不是线性判别分析算法（Linear Discriminant Analysis）。LDA算法由加州伯克利大学计算机系的David M. Blei于2003年发表。目前LDA算法的应用挺广泛，2012年北京举办的SIGKDD国际会议上，在个性化推荐、社交网络、广告预测等各个领域的workshop上都提到LDA模型。LDA算法是以同样出自加州伯克利大学计算机系的Thomas Hufmann于1999年发表的PLSA（Probabilistic Latent Semantic Analysis）为基础，PLSA算法则是对芝加哥大学Scott Deerwester, Susan T. Dumais等人在1990年发表的潜在语义分析（Latent Semantic Analysis，简称LSA）算法思想的吸收。本报告稍后会对PLSA、LSA、LDA三种方法的背景和关联作介绍。

 由于LDA算法是一个用于研究语料库(corpus)的生成模型(generation model)，其理论基础是一元语义模型（unigram model），也就是说，LDA算法的前提是,文档(document)可以被认为是词(word)的集合，忽略任何语法或者出现顺序关系，这个特性也被称为可交换性(Exchangeability)。本文所涉及的PLSA、LSA、LDA三种方法的分析都是在一元语义模型下进行。

本文立足于细节阐释，即在假定读者没有机器学习算法基础的前提下，通过它能迅速了解到LDA算法的思想和实现原理。虽然PLSA目前并没有在工作中被使用，但是它和LDA有很多通用的思想，而且比LDA容易理解，因而也占据较大篇幅。

 

2、三种文本分析方法

    首先统一一下名称。表1列举了LSA算法、PLSA算法、LDA算法各自的简称、全称和别称。为了方便，下文中，我们统一采用简称。

 

  表1三种算法的全称和别名

 

 2.1 LSA算法

在文档的空间向量模型（VSM）中，文档被表示成由特征词出现概率组成的多维向量。这种方法的好处是可以将query和文档转化成同一空间下的向量计算相似度，可以对不同词项赋予不同的权重，在文本检索、分类、聚类问题中都得到了广泛应用。但是空间向量模型的缺点是无法处理一词多义和同义词问题，例如同义词也分别被表示成独立的一维，计算向量的余弦相似度时会低估用户期望的相似度；而某个词项有多个词义时，始终对应同一维度，因此计算的结果会高估用户期望的相似度。

潜在语义分析（LSA）是对传统的空间向量模型（VSM，vector space model）的改进。通过降维，LSA将词和文档映射到潜在语义空间，从而去除了原始向量空间中的一些“噪音”（比如词的误用或者不相关的词偶尔出现在一起），解决了同义词的问题。

    降维是LSA分析的核心。具体做法，是对词项文档矩阵（也叫Term-Document矩阵，以词项(terms)为行, 文档(documents)为列,这里记为C）做SVD分解

设C一共有t行d列, 矩阵的元素为词项的TF-IDF（词频term frequency–反文档频率inverse document frequency）值。然后把的r个对角元素的前k个保留（最大的k个保留）, 后面最小的r-k个奇异值置0, 得到；最后计算一个近似的分解矩阵

   

则是在最小二乘意义下C的最佳逼近，从而得到原始词项文档矩阵的一个低秩逼近矩阵。

    通过在SVD分解近似，我们将原始的向量转化成一个低维隐含语义空间中，起到了特征降维的作用。每个奇异值对应的是每个“语义”维度的权重，将不太重要的权重置为0，只保留最重要的维度信息，去掉一些“噪音”,因而可以得到文档的一种更优表示形式。

 

2.2 PLSA算法

   基于SVD的LSA相比于空间向量模型解决了同义词问题，但是其缺乏严谨的数理统计基础，而且SVD分解非常耗时。另外，LSA没能解决一词多义的问题。

Hofmann于1999年在SIGIR'99提出了基于概率统计的PLSA模型，并且用EM算法学习模型参数。在传统文本分类或聚类模型中，一篇文章（document）只有一个topic（姑且翻译成主题）,而Hofmann提出，一篇文章可以有多个topic，这就是自然语言处理领域颇具开创性的Topic Model的思想。之所以说LDA算法继承了PLSA的衣钵，一个重要的原因就是LDA在文本建模中继承并且发展了Topic Model。Topic Model目前在自然语言理解和生物信息学方面都有应用。通过增加Topic Model，一个词语可以从属于多个Topic，一个Topic下也有多个词（word），这样就保证了一词多义和同义词的问题都可以在Topic Model下得到解决。按照维基百科的解释，主题模型（Topic Model）就是一类从大量的文档中发掘抽象的“主题”的统计模型。至于Topic的具体理解，有些文章将之称之为主题，有的将之解释成“一个概念，一个方面”。

另外，与LSA依赖于矩阵运算得到结果不同，PLSA算法采用的是机器学习中以概率统计为基础的生成模型（generation model）来做文本建模和理解。这里对生成模型做一下简单的介绍。生成模型，在机器学习中的定义是“显示或者隐式地对输入输出的分布建模”，参考自Bishop的《Pattern Recognition and Machine Learning》。在决策论中，有三种决策方式，分别是对联合概率分布建模、对后验概率建模、和找判别函数。判别模型属于第二种，对后验概率建模，将每个观察值划分到一个类。判别函数法是思路最简单的，直接把观察值通过函数映射到分类。而生成模型，是对先验概率和类条件密度函数建模，然后标准化，进而得到后验概率估计。Bishop的《Pattern Recognition and Machine Learning》提到，决策论中，对于分类问题采用的决策准则是，如果决策目标是使观测值被误分类的概率最小，那么应该选择相应的后验概率最大的分类作为决策。

 

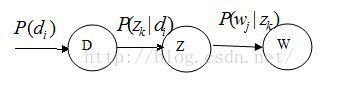
Hofmann提出的PLSA的概率图模型如下

 

 其中D代表文档，Z代表隐含类别或者主题，W为观察到的单词，表示单词出现在文档的概率，表示文档di中出现主题zk下的单词的概率，给定主题Zk出现单词Wj的概率。并且每个主题在所有词项上服从Multinomial （多项式）分布，每个文档在所有主题上服从Multinomial （多项式）分布。

 

    关于这里的两个关于多项式分布的选择，是有其理论依据的。以每个主题在所有词项上服从Multinomial （多项式）分布为例，主要是基于：

1）在同一个主题下，每个词项的产生都可以看成一次从该主题下的所有候选词项中随机挑选出一个词项的试验。不难发现，试验之间是相互独立的。在一元语义模型下，词项之间的顺序不影响其联合分布概率，也就是如果在一个主题下选择了V个词项，那么。举一个例子，如果先挑选词项w1，后挑选词项w2，其概率为，反过来，先挑选词项w2，后挑选词项w1，其概率为，不难看到。

2）每个词项都需只能从从属于该主题的词项中选择。这一条在Topic Model下是很自然的。

3）在不同的试验中，同一个词项被选中的概率是相同的。这一条是在使用多项式分布的时候需要注意的，如果不能保证，多项式分布满足不了。但是这句话不要被错误理解成“在同一次的试验中，不同词项被选中的概率是相同的”。

 

整个文档的生成过程是这样的：

(1) 以的概率选中文档；

(2) 以的概率选中主题；

(3) 以的概率产生一个单词。

我们可以观察到的数据就是对，而zk是隐含变量。的联合分布是

而，分别对应两组Multinomial 分布，我们需要估计这两组分布的参数。PLSA采用EM算法来做估计。

   需要说明的是，PLSA有时会出现过拟合的现象。所谓过拟合（Overfit），是这样一种现象：一个假设在训练数据上能够获得比其他假设更好的拟合，但是在训练数据外的数据集上却不能很好的拟合数据。此时我们就叫这个假设出现了Overfit的现象。出现这种现象的主要原因是训练数据中存在噪音或者训练数据太少。PLSA通过采用tempering heuristic来平滑参数，但是实际应用时，即使采用此方法，过拟合现象仍可能发生。

这里补充一个小插曲，Hofmann在他2004年的论文Latent semantic models for collaborative filtering中指出，他自然知道弄成LDA这种fully bayesian model更漂亮，可是为了避免高时间复杂度，他使用了tempered EM。

PLSA是LSA的概率学延伸，这样说的依据是，LSA的核心思想是降维，只是基于SVD分解的LSA方法是借助于矩阵分解降维，而PLSA是借助于引进Topic层降维。

PLSA中，求解两个多项式分布的参数，是求解的关键。注意到，对应每个文档在所有主题上所服从的多项式分布的参数，而di就表示第i个文档，所以我们可以看到这个参数的规模是随着文档数的增加而增加的。在下文中，我们会看到LDA算法的参数是和文档数无关的，只和Topic个数以及以及字典中term个数有关。

 

表2   LSA和PLSA的相同点和不同点

  

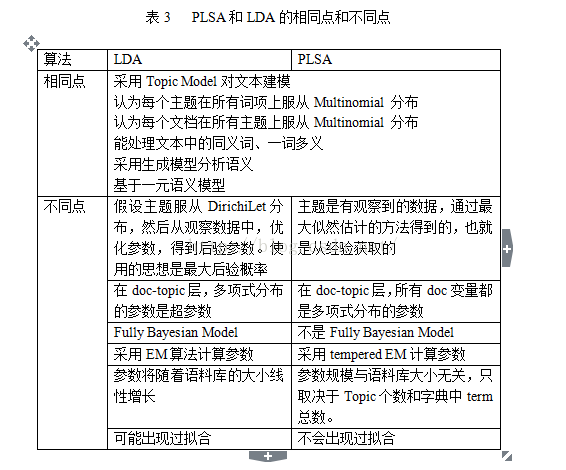
2.3 LDA算法与PLSA的关联和区别

   PLSA在文档级别没有提供一个概率模型，PLSA中每篇文档表示成一系列的主题数目，对于这些数目没有生成概率模型，将导致两个问题：

1） 模型的参数将随着语料库（corpus）的大小线性增长，继而导致过拟合的严重问题。

2） 不清楚如何对于训练集外的文档进行主题分配。

   关于“参数线性增长是如何导致过拟合”的问题，现有的论文和资料都没有做过详细解释，其实这里只举一个小例子就可以阐明。在基于最小二乘法，采用多项式拟合数据点的时候，可能使用的多项式次数高以后，最小二乘误差会最小的，但是，多项式的次数选取的过高，会出现严重的过拟合问题，在对后续数据点做预测的时候完全不可用。而这里的多项式的次数过高，会直接造成拟合时采用的参数过多（拟合一元N次多项式需要N+1个参数），实际上也是参数过多造成数据拟合时出现过拟合的一种情形。

   鉴于PLSA的局限性，LDA算法应运而生。前面提到，LDA算法继承了PLSA中采用生成模型的思路，延续了Topic Model的思想，自然LDA也具有解决一词多义和同义词问题的能力。此外，LDA也延续了PLSA中文档、主题、词项的生成过程，认为每个主题在所有词项上服从Multinomial 分布，每个文档在所有主题上服从Multinomial 分布，采用多项式分布的合理性在2.2中已经详尽说明。   

LDA的参数规模只取决于Topic个数和字典中term总数。LDA在document到topic一层引入了Dirichlet分布，这是它优于PLSA的地方，使得模型参数的数量不会随着语料库的扩大而增多。

这里取Dirichlet分布的依据是什么？首先需要说明，Dirichlet分布是多项分布的共轭先验(Conjugate priors)，也就是说，先验分布为Dirichlet分布，似然函数为多项分布，那么后验分布仍为Dirichlet分布（《模式识别与机器学习》117页有证明）。但是，共轭先验又有什么好处呢？David M. Blei在文章里面说，这样的好处是fancy，或者说，“好算”。或许，这个好算也不够准确，准确的说法是“能算”，也就是在共轭的前提下，这个问题可以通过编程实现求解。无论是Variational inference方法还是Gibbs Sampling都是在前面共轭的条件保证下的计算方法。所以，如果没有Dirichlet分布，后面这些推导可能都不知道怎么算。LDA把一个几乎没法求解的东西解出来了，而且极大的推动了变分推断这个东西。因此，在很多LDA的资料里都会不加解释地说，“选择Dirichlet分布是因为其共轭特性大大减小了计算量”。

PLSA的主题是有观察到的数据，通过最大似然估计的方法得到的，也就是从经验获取的。而LDA是假设主题服从Dirichilet分布，然后从观察数据中，优化参数，得到后验参数，使用的思想是最大后验概率。前者是频率学派的思想，后者是贝叶斯学派的思想。

 

 

参考文献

[1]Patter Recognition and Machine Learning ,Christopher M. Bishop

[2]Latent Dirichlet Allocation,David M. Blei,Journal of Machine Learning Research 3 (2003) 993-1022

[3]Parameter estimation for text analysis,Gregor Heinrich

本文转载自 微信公众号  “机器学习之家”