统计学习方法笔记---朴素贝叶斯
朴素贝叶斯
机器学习实战代码详见:https://editor.csdn.net/md?articleId=105165351
优缺点
优点:
- 在数据较少的情况下仍然有效;
- 可以处理多类别问题
缺点:
- 对于输入数据的准备方式较为敏感?
适用数据类型: 标称型数据
本章概要
-
朴素贝叶斯是典型的生成模型。生成方法由训练数据学习联合概率分布 P ( X , Y ) P(X,Y) P(X,Y),然后求得后验概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X),具体来说,利用训练数据 P ( X ∣ Y ) P(X|Y) P(X∣Y)和 P ( Y ) P(Y) P(Y)的估计,得到联合概率分布:
P ( X , Y ) = P ( Y ) P ( X ∣ Y ) P(X,Y) = P(Y)P(X|Y) P(X,Y)=P(Y)P(X∣Y)
概率估计方法可以是极大似然估计或贝叶斯估计。具体证明见以公式证明1,2。 -
朴素贝叶斯法的基本假设是条件独立性:
P ( X = x ∣ Y = c k ) = P ( X ( 1 ) = x ( 1 ) , . . . , X ( n ) = x ( n ) ∣ Y = c k ) = ∏ j = 1 n P ( X ( j ) = x ( j ) ∣ Y = c k ) P(X = x | Y = c_k) = P(X^{(1)} = x^{(1)}, ..., X^{(n)} = x^{(n)} | Y = c_k) \\ = \prod_{j=1}^nP(X^{(j)} = x^{(j)} | Y = c_k) P(X=x∣Y=ck)=P(X(1)=x(1),...,X(n)=x(n)∣Y=ck)=j=1∏nP(X(j)=x(j)∣Y=ck)
这是一个较强的假设,由于这一假设,模型包含的条件概率的数量大为减少,朴素贝叶斯法的学习与预测大为简化。因为朴素贝叶斯高效,且易于实现。其缺点是分类的性能不一定很高。 -
朴素贝叶斯利用贝叶斯定理与学到的联合概率模型进行分类预测。
后 验 概 率 : P ( Y ∣ X ) = P ( X , Y ) P ( X ) = P ( Y ) P ( X ∣ Y ) ∑ Y P ( Y ) P ( X ∣ Y ) P ( Y = c k ∣ X = x ) = P ( Y = c k ) ∏ j = 1 n P ( X j = x ( j ) ∣ Y = c k ) ∑ k P ( Y = c k ) ∏ j = 1 n P ( X j = x ( j ) ∣ Y = c k ) 后验概率:P(Y|X) = \frac {P(X,Y)} {P(X)} = \frac {P(Y)P(X|Y)} {\sum_Y P(Y)P(X|Y)} \\ \quad \\ P(Y = c_k|X = x)= \frac {P(Y=c_k) \prod_{j=1}^n P(X_j = x^{(j)} | Y = c_k)} {\sum_k{P(Y=c_k) \prod_{j=1}^n P(X_j = x^{(j)} | Y = c_k)}} 后验概率:P(Y∣X)=P(X)P(X,Y)=∑YP(Y)P(X∣Y)P(Y)P(X∣Y)P(Y=ck∣X=x)=∑kP(Y=ck)∏j=1nP(Xj=x(j)∣Y=ck)P(Y=ck)∏j=1nP(Xj=x(j)∣Y=ck)
将输入x分到后验概率最大的类y。
y = a r g m a x c k P ( Y = c k ) ∏ j = 1 n P ( X j = x ( j ) ∣ Y = c k ) y = arg max_{c_k}P(Y=c_k) \prod_{j=1}^n P(X_j = x^{(j)} | Y = c_k) y=argmaxckP(Y=ck)j=1∏nP(Xj=x(j)∣Y=ck) -
后验概率最大等价于0-1损失函数时的期望风险最小化。
算法流程
- 计算先验概率和条件概率:
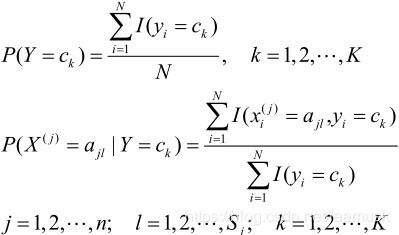
- 对于给定的实例 x = ( x ( 1 ) , x ( 2 ) , … , x ( n ) ) T x=(x^(1) ,x^(2) ,…,x^(n) )^T x=(x(1),x(2),…,x(n))T,计算:

- 确定实例x的类
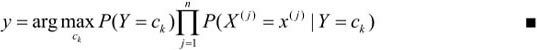
这里需要关注的是当训练集较小时, P ( X ( j ) = a j l ∣ Y = c k ) = ∑ i = 1 N I ( x i ( j ) = a j l , y i = c k ) ∑ i = 1 N I ( y i = c k ) P(X^(j) = a_{jl} | Y = c_k) = \frac {\sum_{i=1}^N I(x_i^{(j)} = a_{jl}, y_i = c_k)} {\sum_{i=1}^N I(y_i = c_k)} P(X(j)=ajl∣Y=ck)=∑i=1NI(yi=ck)∑i=1NI(xi(j)=ajl,yi=ck) 可能等于0, 导致后验概率也为0,所以加上 l a m b d a lambda lambda,即使用贝叶斯估计计算的概率估计方式,能够避免这种情况的出现。
贝叶斯估计法计算出的概率估计如下:
先验概率:
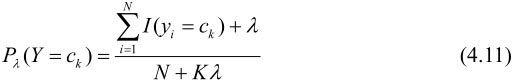
条件概率:

公式推导(仅用于理解,不严谨)
- 用极大似然估计法推出朴素贝叶斯法中的概率估计公式
Y ∈ { C 1 , C 2 , . . . , C k } Y \in {\{C_1, C_2, ... , C_k\}} Y∈{C1,C2,...,Ck}服从多项分布,对于每一个 C i C_i Ci都有对应的概率:
C 1 , C 2 , . . . , C k θ 1 , θ 2 , . . . , θ k ( ∑ i = 1 k θ i = 1 ) C_1, C2, ... , C_k \\ \qquad\qquad\qquad\theta_1, \theta_2, ... , \theta_k \quad(\sum_{i=1}^k \theta_i = 1) C1,C2,...,Ckθ1,θ2,...,θk(i=1∑kθi=1)
将 k k k 个 θ i \theta_i θi 记为一个向量 Θ \Theta Θ = ( θ 1 , θ 2 , . . . , θ k ) (\theta_1, \theta_2, ... , \theta_k) (θ1,θ2,...,θk)
Y Y Y的分布则为:
P ( Y = y ∣ Θ ) = θ 1 I ( y = c 1 ) ⋅ θ 2 I ( y = c 2 ) ⋅ . . . ⋅ θ k I ( y = c k ) = θ i ( 如 果 y = c i ) P(Y=y|\Theta)=\theta_1^{I(y=c_1)} \cdot \theta_2^{I(y=c_2)} \cdot ... \cdot \theta_k^{I(y=c_k)} = \theta_i \quad (如果 y = c_i) P(Y=y∣Θ)=θ1I(y=c1)⋅θ2I(y=c2)⋅...⋅θkI(y=ck)=θi(如果y=ci)
现有样本: y 1 , y 2 , . . . , y N y_1, y_2, ... ,y_N y1,y2,...,yN
联合概率分布:
P ( y 1 , y 2 , . . . , y N ) = P ( y 1 ∣ Θ ) P ( y 2 ∣ Θ ) . . . P ( y N ∣ Θ ) = θ 1 m 1 ⋅ θ 2 m 2 ⋅ . . . ⋅ θ k m k ( m 1 + m 2 + . . . + m k = N ) ( m i 表 示 y = c i 的 次 数 ) P(y_1, y_2, ... ,y_N) = P(y_1 | \Theta) P(y_2 | \Theta)... P(y_N | \Theta) =\theta_1^{m_1} \cdot \theta_2^{m_2} \cdot ... \cdot \theta_k^{m_k} \\ \quad \\ ( m_1 + m_2 + ... + m_k = N) \\ (m_i 表示 y = c_i的次数) P(y1,y2,...,yN)=P(y1∣Θ)P(y2∣Θ)...P(yN∣Θ)=θ1m1⋅θ2m2⋅...⋅θkmk(m1+m2+...+mk=N)(mi表示y=ci的次数)
极大似然估计就是极大化联合概率分布,即
m a x P ( y 1 , y 2 , . . . , y N ) ∣ Θ ) = > m a x l n P ( ⋅ ) = m 1 l n θ 1 + m 2 l n θ 2 + . . . + m k l n θ k s . t θ 1 + . . . + θ k = 1 = > m a x m 1 l n ( θ 1 ) + m 2 l n ( θ 2 ) + . . . + m k l n ( θ k ) + λ ( θ 1 + . . . + θ k ) max \ P(y_1, y_2, ... ,y_N) | \Theta) \\ => max \ lnP(\cdot) = m_1ln\theta_1 + m_2ln\theta_2 + ... + m_kln\theta_k \quad s.t \ \theta_1 + ... + \theta_k = 1 \\ =>max \ m_1ln(\theta_1) + m_2ln(\theta_2) + ... + m_kln(\theta_k) + \lambda(\theta_1 + ... + \theta_k) max P(y1,y2,...,yN)∣Θ)=>max lnP(⋅)=m1lnθ1+m2lnθ2+...+mklnθks.t θ1+...+θk=1=>max m1ln(θ1)+m2ln(θ2)+...+mkln(θk)+λ(θ1+...+θk)
分别对 θ 1 , . . . , t h e t a k \theta_1, ... , theta_k θ1,...,thetak求导:
m 1 θ 1 + λ = 0 = > θ 1 = − m 1 λ = m 1 N m 2 θ 2 + λ = 0 = > θ 2 = − m 2 λ = m 1 N . . . m k θ k + λ = 0 = > θ k = − m k λ = m 1 N − m 1 + m 2 + . . . + m k λ = 1 = > λ = − ( m 1 + m 2 + . . . + m k ) = − N \frac {m_1} {\theta_1} + \lambda = 0 \quad => \quad \theta_1 = - \frac {m_1} {\lambda} =\frac {m_1} {N}\\ \frac {m_2} {\theta_2} + \lambda = 0 \quad => \quad \theta_2 = - \frac {m_2} {\lambda}=\frac {m_1} {N} \\ ... \\ \frac {m_k} {\theta_k} + \lambda = 0 \quad => \quad \theta_k = - \frac {m_k} {\lambda} =\frac {m_1} {N}\\ -\frac {m_1 + m_2 + ... + m_k} {\lambda} = 1\quad => \quad \lambda = -(m_1 + m_2 + ... + m_k) = -N θ1m1+λ=0=>θ1=−λm1=Nm1θ2m2+λ=0=>θ2=−λm2=Nm1...θkmk+λ=0=>θk=−λmk=Nm1−λm1+m2+...+mk=1=>λ=−(m1+m2+...+mk)=−N - 用贝叶斯估计法推出朴素贝叶斯法中的概率估计公式
Y ∈ { C 1 , C 2 , . . . , C k } Y \in {\{C_1, C_2, ... , C_k\}} Y∈{C1,C2,...,Ck}服从多项分布,对于每一个 C i C_i Ci都有对应的概率:
C 1 , C 2 , . . . , C k θ 1 , θ 2 , . . . , θ k ( ∑ i = 1 k θ i = 1 ) C_1, C2, ... , C_k \\ \qquad\qquad\qquad\theta_1, \theta_2, ... , \theta_k \quad(\sum_{i=1}^k \theta_i = 1) C1,C2,...,Ckθ1,θ2,...,θk(i=1∑kθi=1)
Θ \Theta Θ的先验:(狄利克雷分布?)
P ( Θ ) = r ( α 1 + . . . + α k ) r ( α 1 ) + . . . + r ( α k ) θ 1 α 1 − 1 θ 2 α 2 − 1 . . . θ k α k − 1 令 α 1 = α 2 = . . . = α k = α P ( Θ ∣ y 1 , y 2 , . . . y N ) = P ( Θ , y 1 , y 2 , . . . y N ) P ( y 1 , y 2 , . . . y N ) ∝ P ( Θ ) P ( ( y 1 , y 2 , . . . y N ) ∝ θ 1 α − 1 θ 2 α − 1 . . . θ k α − 1 θ 1 m 1 θ 2 m 2 . . . θ k m k ∝ θ 1 m 1 + α − 1 θ 2 m 2 + α − 1 . . . θ k m k + α − 1 P ( Θ ∣ y 1 , y 2 , . . . , y N ) = r ( m 1 + α + m 2 + α + . . . + m k + α ) r ( m 1 + α ) r ( m 2 + α ) . . . r ( m k + α ) θ 1 m 1 + α − 1 θ 2 m 2 + α − 1 . . . θ k m k + α − 1 因 为 我 们 需 要 的 是 最 大 化 后 验 概 率 , 所 以 系 数 可 忽 略 , 即 : m a x ( θ 1 m 1 + α − 1 θ 2 m 2 + α − 1 . . . θ k m k + α − 1 ) 求 得 : θ 1 = m 1 + α − 1 m 1 + α − 1 + m 2 + α − 1 + . . . + m k + α − 1 = m 1 + α − 1 N + k α − k θ i = m i + α − 1 N + k ( α − 1 ) ( λ = α − 1 ) P(\Theta) = \frac {r(\alpha_1 + ... + \alpha_k)} {r(\alpha_1) + ... + r(\alpha_k)} \theta_1^{\alpha_1 - 1}\theta_2^{\alpha_2 - 1}...\theta_k^{\alpha_k - 1} \\ 令\alpha_1 = \alpha_2 = ... = \alpha_k = \alpha \\ \quad \\ P(\Theta | y_1, y_2, ... y_N) = \frac {P(\Theta , y_1, y_2, ... y_N) } {P(y_1, y_2, ... y_N) } \\ \quad \\ \propto P(\Theta)P((y_1, y_2, ... y_N) \\ \quad \\ \qquad \quad \propto \theta_1^{\alpha-1}\theta_2^{\alpha-1}...\theta_k^{\alpha-1}\theta_1^{m_1}\theta_2^{m_2}...\theta_k^{m_k} \\ \quad \\ \qquad \propto \theta_1^{m_1+\alpha-1}\theta_2^{m_2+\alpha-1}...\theta_k^{m_k+\alpha-1} \\ \quad \\ P(\Theta|y_1, y_2, ..., y_N) = \frac {r(m_1 + \alpha + m_2 + \alpha +... + m_k +\alpha)} {r(m_1+\alpha)r(m_2+\alpha)...r(m_k+\alpha)} \theta_1^{m_1+\alpha-1}\theta_2^{m_2+\alpha-1}...\theta_k^{m_k+\alpha-1} \\ \quad \\ 因为我们需要的是最大化后验概率,所以系数可忽略,即:\\ \quad \\ max (\theta_1^{m_1+\alpha-1}\theta_2^{m_2+\alpha-1}...\theta_k^{m_k+\alpha-1}) \\ \quad \\ 求得: \\ \quad \\ \theta_1 = \frac {m_1 + \alpha -1} {m_1 + \alpha -1 + m_2 + \alpha -1 + ... + m_k + \alpha -1} \\ \quad \\ =\frac {m_1 + \alpha -1} {N+ k\alpha-k} \\ \quad \\ \theta_i = \frac {m_i + \alpha -1} {N+ k(\alpha-1)} \quad (\lambda = \alpha-1) P(Θ)=r(α1)+...+r(αk)r(α1+...+αk)θ1α1−1θ2α2−1...θkαk−1令α1=α2=...=αk=αP(Θ∣y1,y2,...yN)=P(y1,y2,...yN)P(Θ,y1,y2,...yN)∝P(Θ)P((y1,y2,...yN)∝θ1α−1θ2α−1...θkα−1θ1m1θ2m2...θkmk∝θ1m1+α−1θ2m2+α−1...θkmk+α−1P(Θ∣y1,y2,...,yN)=r(m1+α)r(m2+α)...r(mk+α)r(m1+α+m2+α+...+mk+α)θ1m1+α−1θ2m2+α−1...θkmk+α−1因为我们需要的是最大化后验概率,所以系数可忽略,即:max(θ1m1+α−1θ2m2+α−1...θkmk+α−1)求得:θ1=m1+α−1+m2+α−1+...+mk+α−1m1+α−1=N+kα−km1+α−1θi=N+k(α−1)mi+α−1(λ=α−1)
代码实现
import numpy as np
import pandas as pd
from collections import Counter
"""def main():
x_train = np.array([[1,'S'],[1,'M'],[1,'M'],[1,'S'],[1,'S'],[2,'S'],[2,'M'],[2,'M'],[2,'L'],[2,'L'],[3,'L'],[3,'M'],[3,'M'],[3,'L'],[3,'L']])
y_train = np.array([-1,-1,1,1,-1,-1,-1,1,1,1,1,1,1,1,-1])
c = [1,-1]
A = np.array([[1,2,3],['S','M','L']])
s = np.array([2,'S'])
landa = 1
NB = neiveByeis(x_train,y_train, c, A, landa)
prediction = NB.predict(s)
print("s{}被分类为:{}".format(s,prediction))
class neiveByeis():
def __init__(self, x_train, y_train, c, A, landa):
self.x_train = x_train
self.y_train = y_train
self.A = A
self.c = c
self.landa = landa
def predict(self,s):
# 首先需要计算 p(y=c1), p(y=c2)...
prediction_y = Counter(self.y_train)
res = dict()
p_c = []
for i in range(len(self.c)):
count = [0] * len(s)
p_c.append((prediction_y[self.c[i]] + self.landa) / (len(self.y_train) + (self.landa * len(self.c))))
res[self.c[i]] = p_c[i]
for j in range(len(self.x_train)):
if self.y_train[j] == self.c[i]:
for k in range(len(s)):
if self.x_train[j][k] == s[k]:
count[k] += 1
print("count:", count)
for n in range(len(s)):
res[self.c[i]] *= ((count[n] + self.landa) / (prediction_y[self.c[i]] + (self.landa * len(self.A[i]))))
print("{} 的概率为:{}".format(self.c[i],res[self.c[i]]))
return max(res, key=res.get)
if __name__=="__main__":
main()
"""
# 优化版本:
class NaiveBayes():
def __init__(self, lambda_):
self.lambda_ = lambda_
self.y_types_count = None # y的(类型:数量)
self.y_types_proba = None # y的(类型:概率)
self.x_types_proba = dict() # (xi 的编号,xi的取值, y的类型):概率
def fit(self, x_train, y_train):
self.y_types = np.unique(y_train) # y的所有取值类型[1,2,3]
X = pd.DataFrame(x_train) # 转化为pandas DataFrame数据格式,下同
y = pd.DataFrame(y_train)
# y 的(类型:数量)统计
self.y_types_count = y[0].value_counts()
# y 的(类型:概率)计算
self.y_types_proba = (self.y_types_count+self.lambda_) / (y.shape[0] + len(self.y_types) * self.lambda_)
# (xi 的编号, xi的取值, y的类型): 概率的计算
for idx in X.columns: # 遍历Xi
print("第 {} 个特征: ".format(idx))
for j in self.y_types: # 选取每一行的y的类型
p_x_y = X[(y==j).values][idx].value_counts() # 选择所有y==j为真的数据点的idx个特征的值
print("在 y = {} 时,对样本第 {} 个特征的频次的统计:\n {}".format(j, idx, p_x_y))
for i in p_x_y.index: # 计算(xi的编号,xi的取值, y的类型):概率
# print("第 {} 个特征的值为:{}".format(idx, i))
# 存储在y = j的情况下,第idx个特征的值为i的样本出现的概率(贝叶斯估计)
self.x_types_proba[(idx,i,j)] = (p_x_y[i]+self.lambda_)/(self.y_types_count[j]+p_x_y.shape[0])
print("--------------")
def predict(self,X_new):
res = []
for y in self.y_types: # 遍历y的可能取值
p_y = self.y_types_proba[y] # 获取y的模型P(Y=Ck)
p_xy = 1
for idx, x in enumerate(X_new):
p_xy *= self.x_types_proba[(idx,x,y)] # 计算P(X=(x1,x2...)/Y=Ck)
res.append(p_y*p_xy)
for i in range(len(self.y_types)):
print("[{}]对应的概率:{:.2%}".format(self.y_types[i],res[i]))
# 返回最大后验概率对应的y值
return self.y_types[np.argmax(res)]
def main():
x_train = np.array([[1,'S'],[1,'M'],[1,'M'],[1,'S'],[1,'S'],[2,'S'],[2,'M'],[2,'M'],[2,'L'],[2,'L'],[3,'L'],[3,'M'],[3,'M'],[3,'L'],[3,'L']])
y_train = np.array([-1,-1,1,1,-1,-1,-1,1,1,1,1,1,1,1,-1])
clf = NaiveBayes(lambda_ = 0.2)
clf.fit(x_train, y_train)
clf.fit(x_train, y_train)
X_new = np.array([2,'S'])
y_predict = clf.predict(X_new)
print("{} 被分类为:{}".format(X_new, y_predict))
if __name__=="__main__":
main()
(2)调用sklearn
def main():
x_train = np.array([[1,'S'],[1,'M'],[1,'M'],[1,'S'],[1,'S'],[2,'S'],[2,'M'],[2,'M'],[2,'L'],[2,'L'],[3,'L'],[3,'M'],[3,'M'],[3,'L'],[3,'L']])
y_train = np.array([-1,-1,1,1,-1,-1,-1,1,1,1,1,1,1,1,-1])
x_new = np.array([[2,'S']])
landa = 1
# 对数据进行预处理
enc = preprocessing.OneHotEncoder(categories='auto')
enc.fit(x_train)
x_train = enc.transform(x_train).toarray()
clf = MultinomialNB(alpha=0.0000001)
clf.fit(x_train, y_train)
x_new = enc.transform(x_new).toarray()
y_prediction = clf.predict(x_new)
print("s {} 被分类为:{}".format(x_new, y_prediction))
print("属于不同分类的概率:{}".format(clf.predict_proba(x_new)))
if __name__=="__main__":
main()

