OpenCV图像直方图

OpenCV图像直方图

微信公众号：幼儿园的学霸
个人的学习笔记，关于OpenCV,关于机器学习, …。问题或建议，请公众号留言;

灰度直方图(Histogram)是数字图像处理中最简单、最有用的工具之一，它概括了一幅图像的灰度级内容此处对直方图的数学原理以及OpenCV中的示例进行了展示。

目录

定义

灰度直方图（histogram）是灰度级的函数，描述的是图像中每种灰度级像素的个数，反映图像中每种灰度出现的频率。横坐标是灰度级，纵坐标是灰度级出现的频率（对数字图像来说，意味着该灰度级像素的个数）。

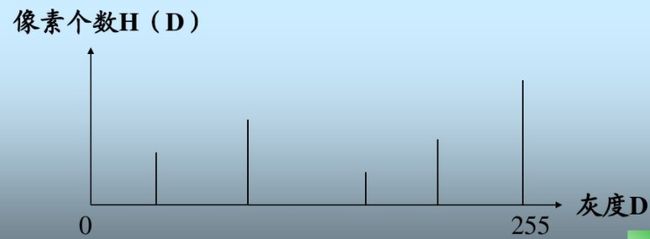
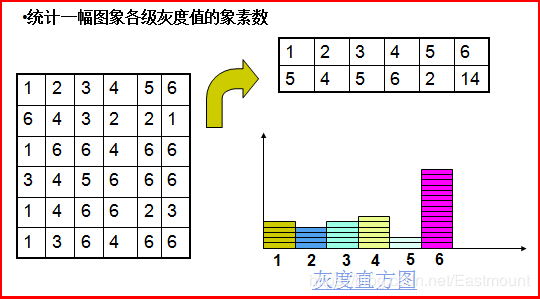
过通常会将纵坐标归一化到[0,1]区间内，也就是将灰度级出现的频率（像素个数）除以图像中像素的总数。

对于连续图像，平滑地从中心的高灰度级变化到边缘的低灰度级。直方图定义为：
$$H(D)=\underset{\Delta D\to 0}{\lim }\frac{A(D)-A(D+\Delta D)}{\Delta D}=-\frac{d}{\Delta D}A(D)-----(1)$$
其中$A(D)$为阈值面积函数：为一幅连续图像中被具有灰度级D的所有轮廓线所包围的面积。
上式说明，一幅连续图像的直方图是其面积函数的导数的负值。
若将图像看成是二维随机变量，则面积函数相当于其累计分布函数，灰度直方图相当于其概率密度函数。

根据上式介绍的对直方图的定义，对公式进行积分：
$${\int }_D^{\infty }H(D)dD=[-A(D){]}_D^{\infty }=A(D)$$
即为图像总面积。
对于离散图像：
$$\sum _0^{255}=NL\ast NS=the.total.pixe{l}^{\prime }s.of.image$$
即为图像总的像素数。

回到式(1),对于离散函数，固定$\Delta D$为1，则：
$$H(D)=A(D)-A(D+1)$$
显然：对数字图像，任一灰度级D的面积函数就是大于或等于灰度级D的像素的个数。灰度直方图的计算公式如下：
$$p(r_k)=\frac{n_k}{M\ast N}$$
其中， $r_k$是像素的灰度级，$n_k$是具有灰度级$r_k$的像素的个数，$M,N$是图像中总的像素个数。

直方图的绘制

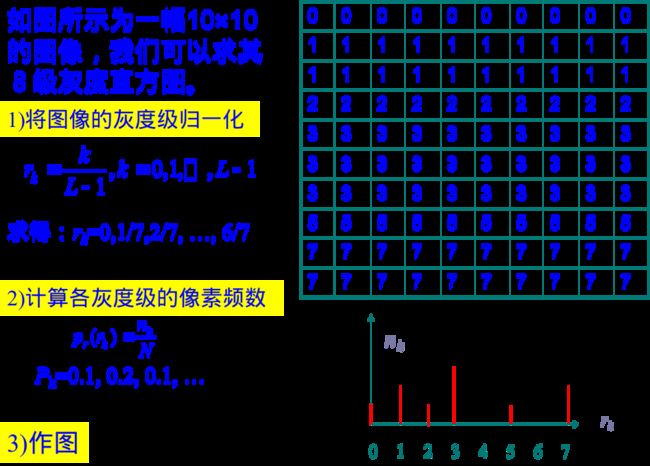
1) 将图像的灰度归一化
若图像的灰度级为0,1,……,L-1,令
$r_k=\frac{k}{L-1},k=0,1,\cdots ,L-1$
则$0\le r_k\le 1$,L为灰度级的层数，$\Delta L_k=r_{k+1}-r_k$为灰度间隔。
2)计算各灰度级的像素频数（或概率）
设$n_k$表示灰度级为$r_k$的像素的个数，$N$为总的像素个数，计算像素频数的公式为：
$p_r(r_k)=\frac{n_k}{N}$
3)作图
建立直角坐标系，横轴表示灰度级$r_k$的取值，纵轴表示灰度级对应的概率$p_r(r_k)$

下面为对一幅10X10的图像求其8级灰度直方图的示例

直方图的性质

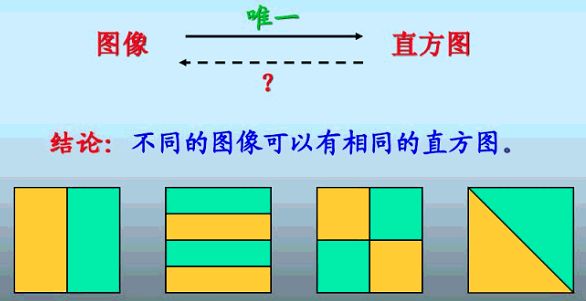
1）图像被缩减成直方图后，所有的空间信息都丢失了，也就是说，直方图不能提供像素在图像中的位置信息。因此不同的图像可以有相同的直方图。

2）如果一幅图像包含一个灰度均匀一致的物体，且背景与物体的对比度很强，规定物体的边界时由灰度级$D_1$定义的轮廓线。

3)如果一幅图像由几个连接但不交叠（当然也不能有遗漏）的区域组成，每个区域的直方图已知，则整个图像的直方图是该几个区域的直方图之和。

直方图的应用

在使用轮廓线确定物体边界时，通过直方图更好的选择边界阈值，进行阈值化处理；对物体与背景有较强对比的景物的分割特别有用；简单物体的面积和综合光密度IOD可以通过图像的直方图求得。
1)数字化参数
可用来判断一幅图像是否合理地利用了全部被允许的灰度级范围。一幅图像应利用几乎全部的灰度级。

2)边界阈值选取
1°确立图像中简单物体的边界，用于物体与背景有较强对比时的景物分割
2°阈值化：使用轮廓线作为边界的技术

OpenCV计算并绘制灰度直方图

函数声明

直方图的计算是很简单的，无非是遍历图像的像素，统计每个灰度级的个数。在OpenCV中封装了直方图的计算函数calcHist，为了更为通用，该函数的参数有些复杂，其声明如下：

calcHist(
const Mat* images,//输入图像的数组，这些图像要有仙童大小、深度（CV_8U,CV_16U,CV_32F）
int images,// 图像数目
const int* channels,// 通道数，要计算的通道数的下标，可以传一个数组 {0, 1} 表示计算第0通道与第1通道的直方图，此数组长度要与histsize ranges 数组长度一致
InputArray mask,//输入mask，可选。如有，则表示只计算mask元素值为非0的位置的直方图
OutputArray hist,//输出的直方图数据
int dims,// 直方图的维度
const int* histsize,//在每一维上直方图的个数。
                //简单把直方图看作一个一个的竖条的话，就是每一维上竖条的个数。
const float* ranges,// 直方图每个维度要统计的灰度级的范围
bool uniform,// true by default 是否归一化
bool accumulate// false by defaut
)

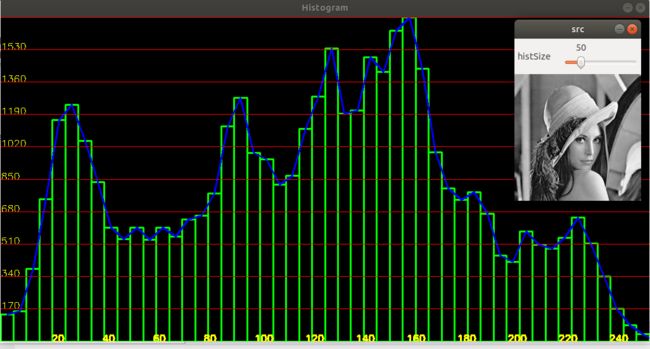
代码演示

下面这段代码展示了利用calcHist函数计算直方图，及动态调整直方图“竖条”的个数的过程。

//====================================================================//
// Created by liheng on 19-3-6.
//Program:图像灰度直方图示例,及动态调整“竖条”数量，观察直方图效果
//Data:2019.3.6
//Author:liheng
//Version:V1.0
//====================================================================//

#include 


cv::Mat src;//需要计算直方图的灰度图像
cv::Mat histimg;//进行直方图展示的图
cv::MatND hist;//计算得到的直方图结果

int histSize = 50;     // 划分HIST的初始个数，越高越精确

//滚动条函数
void HIST(int t,void*)
{
    char string[10];

    if(histSize==0)
    {
        printf("直方图条数不能为零！\n");
    }
    else
    {
        int dims = 1;
        float hranges[2] = {0, 255};
        const float *ranges[1] = {hranges};   // 这里需要为const类型
        int channels = 0;

        histimg.create(512,256*4,CV_8UC3);
        histimg.setTo(cv::Scalar(0,0,0));

        //计算图像的直方图
        calcHist(&src, 1, &channels, cv::Mat(), hist, dims, &histSize, ranges);    // cv 中是cvCalcHist
        //normalize(hist, hist, 0, histimg.rows*0.5, NORM_MINMAX, -1, Mat());//将直方图归一化，防止某一条过高，显示不全


        double maxVal = 0;
        cv::Point maxLoc;
        cv::minMaxLoc(hist, NULL, &maxVal, NULL, &maxLoc);//寻找最大值及其位置


        double bin_w =(double) histimg.cols / histSize;  // histSize: 条的个数，则 bin_w 为条的宽度
        double bin_u = (double)histimg.rows/ maxVal;  // maxVal: 最高条的像素个数，则 bin_u 为单个像素的高度

        // 画直方图
        for(int i=0;i(i);           //   注意hist中是float类型
            cv::Point p1=cv::Point((i+1)*bin_w,histimg.rows-binValue*bin_u);

            cv::rectangle(histimg,p0,p1,cv::Scalar(0,255,0),2,8,0);
        }

        //曲线形式的直方图
        for (int i = 0; i < histSize; i++)
        {
            cv::line(histimg,
                    cv::Point(bin_w*i+bin_w/2, histimg.rows-hist.at(i)*bin_u),
                    cv::Point(bin_w*(i+1)+bin_w/2, histimg.rows-hist.at(i+1)*bin_u),
                    cv::Scalar(255, 0, 0), 2, 8, 0);//bin_w/2是为了保证折现位于直方图每条的中间位置
        }

        //画纵坐标刻度（像素个数）
        int kedu=0;
        for(int i=1;kedu

运行效果如下：

扩展

利用直方图，还可以对图像进行直方图均衡化和规范化的操作。

直方图均衡化

大多数自然图像，其灰度分布集中在较窄的区间，引起图像细节不够清晰，采用直方图修正后可使图像的灰度间距拉开或使灰度分布均匀，从而增大反差，使图像细节清晰，达到增强的目的。例如一幅过曝光的图片，其灰度级都集中在高亮度范围内，而曝光不足的图片，其灰度集中在低亮度范围内，具有这样直方图的图片其可视效果比较差。
直方图均衡化方法的基本思想是，对在图像中像素个数多的灰度级进行展宽，而对像素个数少的灰度级进行缩减。从而达到清晰图像的目的，增强图像的整体对比度。
其基本处理思路是，把原始图像的灰度直方图从比较集中的某个灰度区间变成在全部灰度范围内的均匀分布。即在每个灰度级上都具有相同像素点数的过程。

直方图规范化

直方图均衡化的优点是能自动增强整个图像的对比度，但它的具体增强效果不易控制，处理的结果总是得到全局的均衡化的直方图。实际工作中，有时需要变换直方图使之成为某个特定的形状，从而有选择地增强某个灰度值范围内的对比度，这时可采用比较灵活的直方图规定化方法。
直方图规范化是指将一幅图像通过灰度转换后，使其具有特定的直方图形式，如使图像与某一标准图像具有相同的直方图，或使图像具有某一特定函数形式的直方图。

---

下面的是我的公众号二维码图片，欢迎关注。