Genetic CNN: 经典NAS算法，遗传算法的标准套用 | ICCV 2017

论文将标准的遗传算法应用到神经网络结构搜索中，首先对网络进行编码表示，然后进行遗传操作，整体方法十分简洁，搜索空间设计的十分简单，基本相当于只搜索节点间的连接方式，但是效果还是挺不错的，十分值得学习
 
来源：晓飞的算法工程笔记 公众号

论文: Genetic CNN

• 论文地址：https://arxiv.org/abs/1703.01513

Introduction

---

  为了进行神经网络架构搜索，论文将网络限制为有限的深度，每层为预设的操作，但仍然存在很多候选网络，为了有效地在巨大的搜索空间中进行搜索，论文提出遗传算法进行加速。首先构造初始种群，然后对种群内的个体进行遗传操作，即选择、交叉和变异，通过识别的准确率来判断其适应性，最终获得强大的种群

Our Approach

---

Binary Network Representation

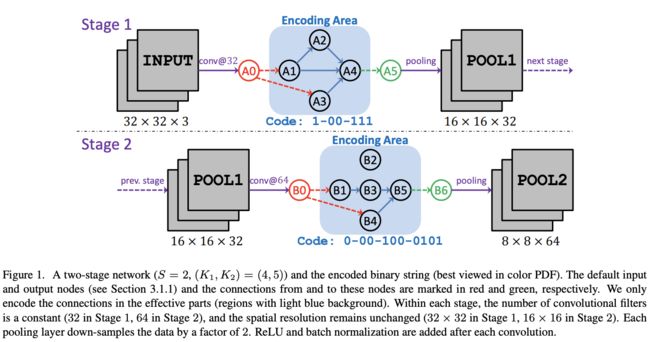
  目前SOTA的网络大都由多个阶段构成，每个阶段内的层具有相同的维度，而相邻的阶段则用池化进行连接。借鉴这种思想，定义网络有$S$个阶段组成，$s$-th阶段($s=1,2,...,S$)包含$K_s$个节点，标记为$v_{s,k}$，$k_s=1,2,...,K_s$，节点按顺序排列，仅允许低序号节点连接到高序号节点，对节点的所有输入进行element-wise sum，每个节点代表卷积操作，卷积后都接BN+ReLU，网络不加入全连接层
  每个阶段使用$1+2+...+(K_s-1)=\frac{1}{2}{K}_s(K_s-1)$位来表示内部连接，第一位表示连接$(v_{s,1},v_{s,2})$，第二位和第三位则表示连接$(v_{s,1},v_{s,3})$和$(v_{s,2},v_{s,3})$，以此类推，最后$K_s-1$位则表示$v_{s,K_s}$与其它节点的连接。对于$1\le i\le j\le K_s$，如果$(v_{s_i},v_{s,j})=1$，则$v_{s_i}$和$v_{s,j}$有边，$v_{s,j}$将$v_{s,i}$的输出作为element-wise sum的一部分。编码如图1所示，但是Stage 2的编码好像有点问题，按照图片应该是0-10-000-0011

• Technical Details

  每个阶段默认有两个节点，分别为输入节点$v_{s,0}$和输出节点$v_{s,K_s+1}$，输入节点使用卷积将前一个阶段的特征进一步提取，然后传递给没有输入的节点中，输出节点则element-wise sum所有没被使用的节点的输出，然后进行一次卷积再接池化层，这里有两种特殊的情况：

• 如果节点$v_{s,i}$被隔离了，没有非默认输入和输出，则直接忽略，如图1 B2节点

• 如果当前阶段没有连接，全部为0，则只进行一次卷积（原本至少输入输出节点都会进行一次）

• Examples and Limitations

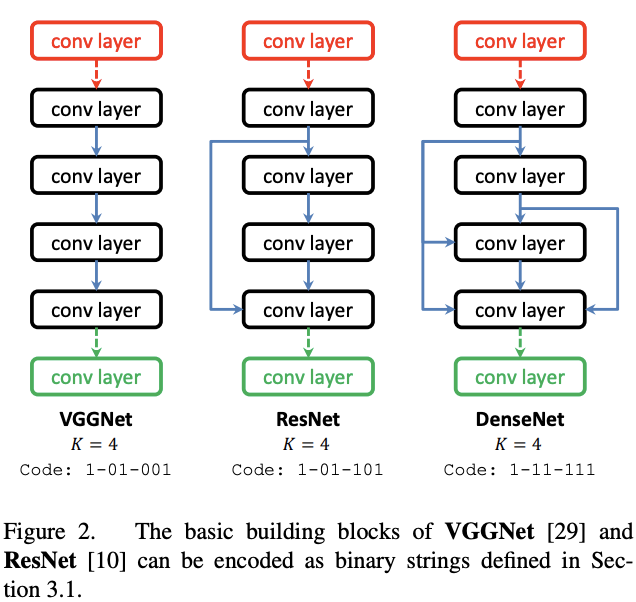
  这样的编码形式可以编码目前的主流分类结构，但也有很多局限性：

• 目前的连接方式只有卷积和池化，不能使用其它比较tricky的模块，例如Maxout
• 每个阶段的卷积核是固定的，阻碍了multi-scale特征的融合

Genetic Operations

  遗传算法过程如图1所示，共进行$T$代遗传，每代包含3个操作，选择、变异和交叉，适应值通过训练后的模型在验证集上获得

• Initialization

  初始化一个随机模型集合$\{{\mathbb{M}}_{0,n}{\}}_{n=1}^N$，每个模型是长度为$L$的二进制串，串上每位服从伯努利分布$b_{0,n}^l\sim \mathcal{B}(0.5)$,$l=1,2,...,L$，然后训练并测试每个模型的准确率，这里的初始化策略影响不大

• Selection

  在每一代种群生成前都会进行选择操作，在$t$-th代前，个体${\mathbb{M}}_{t-1,n}$的适应性为$r_{t-1,n}$，直接影响${\mathbb{M}}_{t-1,n}$在选择阶段存活的概率。具体选择使用俄罗斯轮盘选择法(Russian roulette)，每个个体选取的概率与$r_{t-1,n}-r_{t-1,0}$成比例，$r_{t-1,0}$为上一代的最低适应性。选择后的保持种群总数不变，所以一个个体可能会被选择多次

• Mutation and Crossover

  变异的操作包含对二进制串每个位进行概率为$q_M$的反转，而交叉的操作则同时改变两个个体，以概率$q_C$对个体间的stage进行交换。个体变异的概率为$p_M$，每组个体交叉的概率为$p_C$，具体的操作看算法1，虽然这种方法很简单，但是十分有效

• Evaluation

  在上述操作后，对每个个体${\mathbb{M}}_{t,n}$进行训练以及测试来获得适应值，如果该个体之前已经测试过了，则直接再测一遍然后求平均，这样能移除训练中的不确定性

Experiments

---

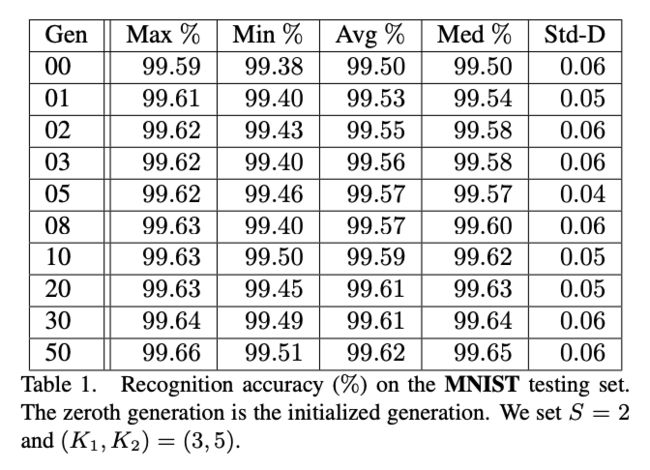
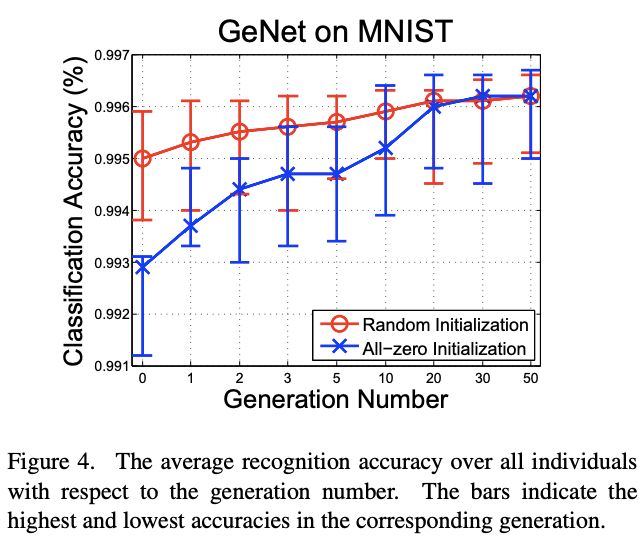
MNIST Experiments

  实验配置，$S=2$，$(K_1,K_2)=(3,5)$，$L=13$，种群初始$N=20$，共一次$T=50$，$p_M=0.8$,$q_M=0.1$,$p_C=0.2$,$q_C=0.3$，一共只产生$20\times (50+1)=1020\le 8192$个网络，耗时2 GPU-day

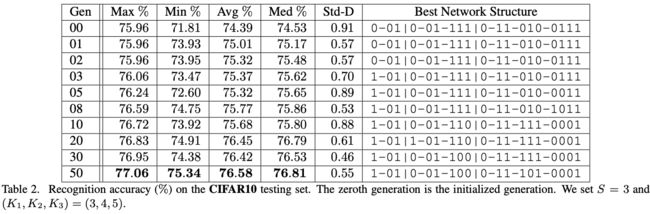
CIFAR10 Experiments

  实验配置，$S=3$，$(K_1,K_2,K_3)=(3,4,5)$，$L=19$，种群初始$N=20$，共一次$T=50$，$p_M=0.8$,$q_M=0.05$,$p_C=0.2$,$q_C=0.2$，一共只产生$20\times (50+1)=1020\le 524288$个网络，耗时17 GPU-day

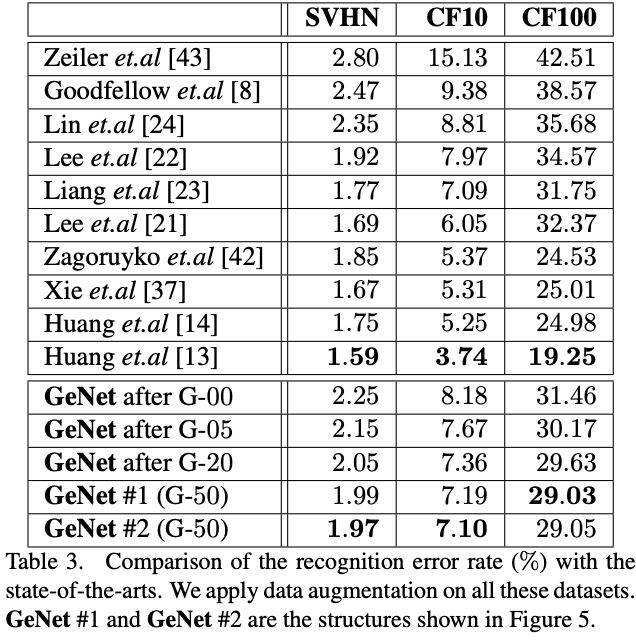
CIFAR and SVHN Experiments

  将CIFAR-10中学习到的网络直接在别的数据集上进行测试

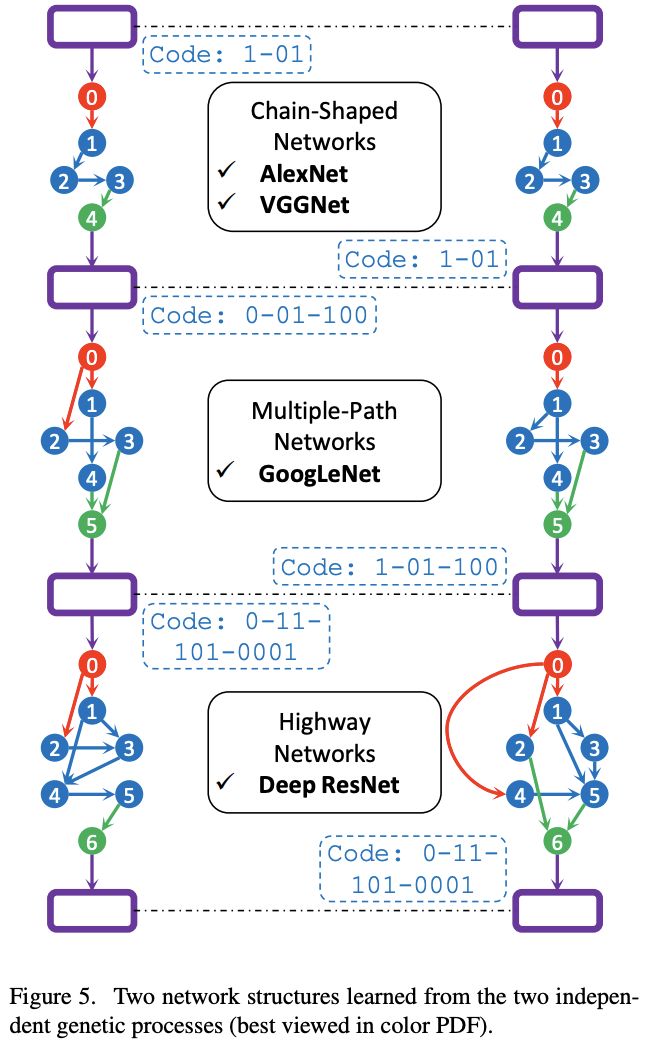
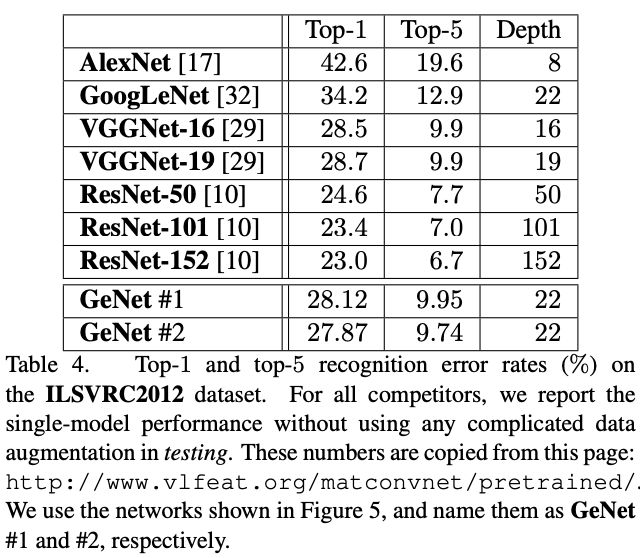
ILSVRC2012 Experiments

  将图5中的两个网络在ILSVRC2012上进行训练，先用VFFNet的stem进行下采样，再过图5的网络，最后接全连接进行分类

CONCLUSION

---

  论文将标准的遗传算法应用到神经网络结构搜索中，首先对网络进行编码表示，然后进行遗传操作，整体方法十分简洁，搜索空间设计的十分简单，基本相当于只搜索节点间的连接方式，但是效果还是挺不错的，十分值得学习

 
 
 

如果本文对你有帮助，麻烦点个赞或在看呗～
更多内容请关注 微信公众号【晓飞的算法工程笔记】