SENet(Squeeze-and-Excitation Networks)论文详解
《Squeeze-and-Excitation Networks》这篇文章在17年就发布在axiv上了,最近一次修改是2019年五月,最近看用的人还是蛮多的,可能是因为效果好而且使用简单吧。
该网络其实可以理解为一个网络中的插件,可以和各种网络配合,如最基础的卷积层,resnet,inception等等。下面来看看它的实现原理。
一、SE块(SQUEEZE-AND-EXCITATION BLOCKS)
SE模块是在一个我们称为 F t r F_{tr} Ftr的变化上建立的,其中 F t r F_{tr} Ftr的输入为 X ∈ R H ′ × W ′ × C ′ X\in R^{H'\times W'\times C'} X∈RH′×W′×C′,输出为 U ∈ R H × W × C U\in R^{H\times W\times C} U∈RH×W×C。
为了便于理解,我们可以将变换 F t r F_{tr} Ftr看成是一个简单的卷积操作,用式子 V = [ v 1 , v 2 , . . . , v C ] V=[v_1,v_2,...,v_C] V=[v1,v2,...,vC]表示,其中 v c v_c vc表示第c个卷积核。那么输出 U = [ u 1 , u 2 , . . . , u C ] U=[u_1,u_2,...,u_C] U=[u1,u2,...,uC]能用下式表示:
u c = v c ∗ X = ∑ s = 1 C ′ v c s ∗ x s u_c=v_c*X=\sum^{C'}_{s=1}v^{s}_{c}*x^{s} uc=vc∗X=∑s=1C′vcs∗xs
上式中*表示卷积, v c = [ v c 1 , v c 2 , . . . , v c C ′ ] v_c=[v^{1}_{c}, v^{2}_{c},...,v^{C'}_{c}] vc=[vc1,vc2,...,vcC′], X = [ x 1 , x 2 , . . . , x C ′ ] X=[x^{1}, x^{2},...,x^{C'}] X=[x1,x2,...,xC′],且 u c ∈ R H × W u_c\in R^{H\times W} uc∈RH×W。 v c s v^{s}_{c} vcs是一个2D空间卷积,这里为了简化没有体现出bias。这里通过卷积层的建模,使得通道间的卷积特征有了一些隐形的提取过程。为了让通道间的特征更好的利用全局信息,在提取到的特征 U U U被送入下一层前,我们提出了两步操作,分别称为squeeze和excitation。
上述公式看起来很麻烦,SE blocks可以很形象用下图表示:
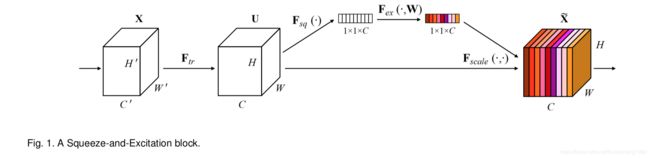
下面来分别介绍一下squeeze和excitation操作。
1.1 Squeeze:: Global Information Embedding
因为每个卷积提取到的特征都是一个局部特征,或者说是个局部的感受野,因此特征 U U U是不能利用感受野外的一些信息。
为了缓解这个问题,我们提出了squeeze操作。它其实就是对提取到的特征,在每个通道上执行全局平均池化(global average pooling)。用公式表示, z ∈ R C z\in R^C z∈RC是对特征 U U U在空间维度 H × W H\times W H×W执行全局平均池化后的结果。对于z的每一个元素表示如下:
z c = F s q ( u c ) = 1 H × W ∑ i = 1 H ∑ j = 1 W u c ( i , j ) z_c=F_{sq}(u_c)=\frac{1}{H\times W}\sum^{H}_{i=1}\sum^{W}_{j=1}u_c(i,j) zc=Fsq(uc)=H×W1∑i=1H∑j=1Wuc(i,j)
1.2 Excitation: Adaptive Recalibration
为了利用squeeze操作的信息和利用通道间的信息依赖,我们接下来使用excitation操作来完成,而且这个操作需要满足两个条件:第一,操作灵活能够获得通道间的非线性关系;第二,学到的关系不一定是互斥的,因为我们希望多个通道特征被加强,而不是像one-hot那种形式,只加强某一个通道特征。
为了满足这两个条件我们采用下式的变换形式:
s = F e x ( z , W ) = σ ( g ( z , W ) ) = σ ( W 2 δ ( W 1 z ) ) s = F_{ex}(z, W) = \sigma(g(z, W)) = \sigma(W_2\delta(W_1z)) s=Fex(z,W)=σ(g(z,W))=σ(W2δ(W1z))
上式中, σ \sigma σ表示sigmoid函数, δ \delta δ表示relu函数, W 1 ∈ R C r × C W_1\in R^{\frac{C}{r}\times C} W1∈RrC×C, W 2 ∈ R C × C r W_2\in R^{C\times\frac{C}{r}} W2∈RC×rC。因为excitation操作有两个全连接层,为了简化操作引入了参数r,r是用来减少全连接层维度的。
得到s后,可以通过下式得到SE block的最终输出
x ~ c = F s c a l e ( u c , s c ) = s c u c \tilde{x}_c=F_{scale}(u_c,s_c)=s_{c}u_{c} x~c=Fscale(uc,sc)=scuc
X ~ = [ x ~ 1 , x ~ 2 , . . . , x ~ C ] \tilde{X}=[\tilde{x}_1, \tilde{x}_2, ...,\tilde{x}_C] X~=[x~1,x~2,...,x~C]
从上式可以看出 F s c a l e F_{scale} Fscale就是通道上的乘积, u c ∈ R H × W u_c\in R^{H\times W} uc∈RH×W。
上述就是SE block的原理,可以看出SE block其实就是一个自注意力(self-attention)的函数。
二、实例化(Instantiations)
之前说是SE block非常的方便,下面来看看SE block怎么应用到各种网络中。
对于VGG来说,可以把每个卷积看成是一个 F t r F_{tr} Ftr变换就可以了。
对于Inception networks来说,可以把一整个Inception module当作是一个 F t r F_{tr} Ftr变换,加入SE block就可以得到SE-Inception network了,如下图表示。
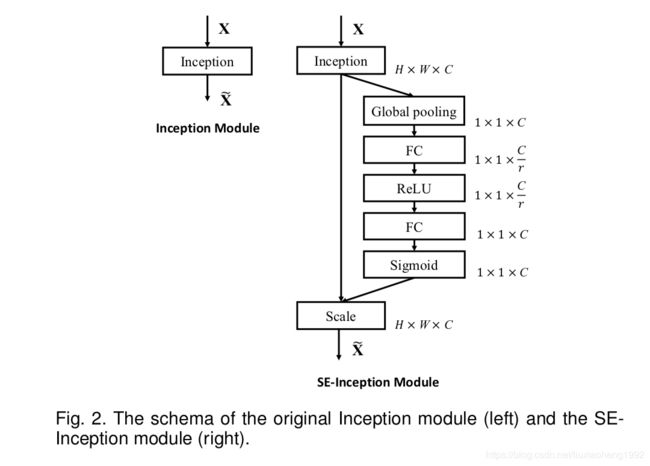
对于residual networks来说,非直连部分可以当作是一个 F t r F_{tr} Ftr变换,如下图所示。
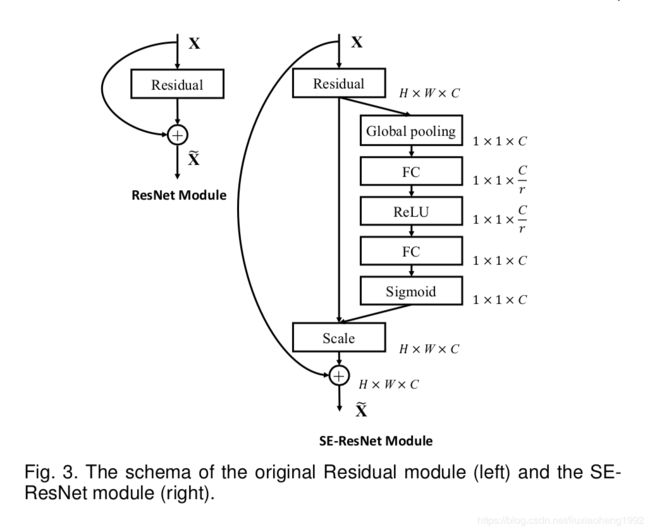
可以看出SE block应用起来很方便,像其他的网络,如Mobilenet、Sufflenet、ResNeXt 等可以作类似的应用。
三、模型的复杂度
拿ResNet-50和SE-ResNet-50对比来说,如果输入的是 224 × 224 224\times 224 224×224大小的图像,ResNet-50一次前向需要∼3.86 GFLOPs大小的计算量。对于SE-ResNet-50,里面的r取16,需要∼3.87 GFLOPs的计算量,可以看出只增加了0.26%的计算量。但是这时候的效果和ResNet-101差不多,效果如下表所示
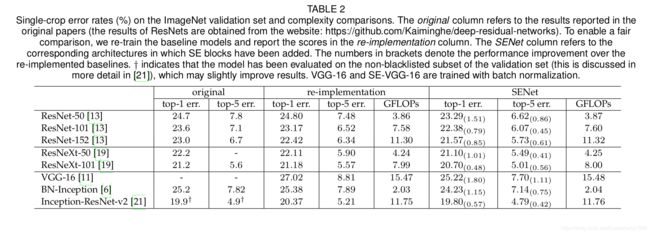
在实际的计算中,对于一台8 NVIDIA Titan X的服务器,当batch设为256时,ResNet-50一次前向和后向的时间是190ms,而SE-ResNet-50需要209ms。推断过程中,对于cpu来说,大小为 224 × 224 224\times 224 224×224的图像ResNet-50需要164ms,SE-ResNet-50需要167ms。
对于SE导致的参数量的计算如下公式表示
2 r ∑ s = 1 S N s ⋅ C s 2 \frac{2}{r}\sum^{S}_{s=1}N_s\cdot C^2_s r2∑s=1SNs⋅Cs2
上式中r是为了减少复制度的超参数,S是网络中stage的个数(可以看resnet的结构,一个stage由几个blockneck组成), C s C_s Cs表示输出的通道数, N s N_s Ns表示第s个stage中block的个数。这里没有计算bias,认为在FC层中,可以忽略不计。
SE-ResNet-50网络中相对于ResNet-50引入了∼2.5 million的参数,而原始ResNet-50就有∼25 million参数量。
相对于增加的效果,增加的参数量和计算量都是可以接受的。
SENet基本就这些内容,文章还有很多实验结果可以查看原文详细了解。
欢迎加入Object Detection交流,群聊号码:910457072