线性回归、lasso回归、岭回归以及弹性网络的系统解释
线性回归、lasso回归、岭回归以及弹性网络的系统解释
- 声明
- 背景介绍
- 概述
- 线性回归模型函数及损失函数
- 线性回归算法
- 多项式回归(线性回归的推广)
- 广义线性回归(线性回归的推广)
- 岭回归(Ridge回归)
- lasso回归
- 为什么lasso回归容易使得不重要的变量的系数变为0而岭回归却会保留它们
- 弹性网络(Elastic Net)
- 结语
- 参考资料
声明
本博客集合了网上众多大牛的博客和观点,后面将对主要的引用源进行列举。在此对各位博主大牛表示感谢,若有侵权,请联系我。
第一次写博客,任何意见,请不吝赐教!
背景介绍
线性回归模型的偏回归系数的表达式: θ = ( X ⊺ X ) − 1 X ⊺ Y \theta =(X^\intercal X)^{−1}X^\intercal Y θ=(X⊺X)−1X⊺Y要能保证该回归系数有解,必须确保XTX矩阵是满秩的,即XTX可逆,但在实际的数据当中,自变量之间可能存在高度自相关性,就会导致偏回归系数无解或结果无效。为了能够克服这个问题,可以根据业务知识,将那些高自相关的变量进行删除;或者选用岭回归也能够避免XTX的不可逆。
(岭回归的必要性还有为了防止过拟合)
岭回归一般可以用来解决线性回归模型系数无解的两种情况,一方面是自变量间存在高度多重共线性,另一方面则是自变量个数大于等于观测个数。针对这两种情况,我们不妨设计两个矩阵,来计算一下XTX的行列式。
比如:第一种矩阵:第一列和第三列存在两倍关系(即多重共线性);第二种矩阵:列数比行数多(非满秩)
所以,不管是高度多重共线性的矩阵还是列数多于观测数的矩阵,最终算出来的行列式都等于0或者是近似为0,类似于这样的矩阵,都会导致线性回归模型的偏回归系数无解或解无意义(因为矩阵行列式近似为0时,其逆将偏于无穷大,导致回归系数也被放大)。那如何来解决这个问题呢?1970年Heer提出了岭回归方法,非常巧妙的化解了这个死胡同,即在 X ⊺ X X^\intercal X X⊺X的基础上加上一个较小的 α \alpha α扰动 (具体做法是在损失函数中加入了线性回归系数的L2正则项),从而使得行列式不再为0。LASSO回归与岭回归非常类似,不同的是在损失函数中加入了线性回归系数的L1正则项。
概述
线性回归问题算是机器学习中最基本的问题了,它主要包含线性回归算法、多项式回归算法(线性回归算法的推广)和广义线性回归(线性回归算法的推广)。
以线性回归为基础,可以衍生出lasso回归、岭回归和弹性回归。线性回归采用误差平方和来作为损失函数,虽然这种算法简单,但是也会出现过拟合的现象,在线性回归损失函数中加入正则项可以有效地解决过拟合问题;线性回归的损失函数中加入自变量系数向量的L1范数后,线性回归变为lasso回归;线性回归的损失函数中加入自变量系数向量的L2范数后,线性回归变为岭回归(Ridge回归);线性回归的损失函数中加入自变量系数的L1范数和L2范数的结合后,线性回归变为弹性网络(Elastic Net)。
线性回归衍生出的三种回归方法各有优缺点,其详细内容后面会一一介绍。
线性回归模型函数及损失函数
线性回归遇到的问题可以做这样的描述,假设我们有m个样本,每个样本 i i i 包含 n n n个特征 x i 1 , x i 2 , . . . , x i n x_{i1},x_{i2},...,x_{in} xi1,xi2,...,xin和一个输出 y i y_i yi,如下: ( x 1 ( 1 ) , x 2 ( 1 ) , . . . , x n ( 1 ) , y 1 ) , ( x 1 ( 2 ) , x 2 ( 2 ) , . . . , x n ( 2 ) , y 2 ) , . . . . . . ( x 1 ( m ) , x 2 ( m ) , . . . , x n ( m ) , y m ) , (x_1^{(1)}, x_2^{(1)}, ...,x_n^{(1)}, y_1),\\(x_1^{(2)}, x_2^{(2)}, ...,x_n^{(2)}, y_2), \\......\\(x_1^{(m)}, x_2^{(m)},...,x_n^{(m)},y_m), (x1(1),x2(1),...,xn(1),y1),(x1(2),x2(2),...,xn(2),y2),......(x1(m),x2(m),...,xn(m),ym),
我们的问题是,当给定一个新的 ( x 1 ( m + 1 ) , x 2 ( m + 1 ) , . . . , x n ( m + 1 ) (x_1^{(m+1)}, x_2^{(m+1)}, ...,x_n^{(m+1)} (x1(m+1),x2(m+1),...,xn(m+1)时,如何确定其对应的输出 y m + 1 y_{m+1} ym+1呢?如果这个问题中的 y y y 是连续的,那么这是一个回归问题,如果 y y y 是离散的,那么这是一个分类问题。
对于 n n n维特征的样本数据,如果我们决定使用线性回归,那么对应的模型是这样的:
h θ ( x 1 , x 2 , . . . , x n ) = θ 0 + θ 1 x 1 + . . . + θ n x n , h_\theta(x_1,x_2,...,x_n)=\theta_0+\theta_1x_1+...+\theta_nx_n, hθ(x1,x2,...,xn)=θ0+θ1x1+...+θnxn,其中 θ i ( i = 0 , 1 , 2... n ) \theta_i (i = 0,1,2... n) θi(i=0,1,2...n)为模型参数, x i ( i = 0 , 1 , 2... n ) x_i (i = 0,1,2... n) xi(i=0,1,2...n)为每个样本的 n n n个特征值。这个表示可以简化,我们增加一个特征 x 0 = 1 x_0=1 x0=1 ,这样
h θ ( x 0 , x 1 , . . . , x n ) = ∑ i = 0 n θ i x i h_\theta(x_0,x_1,...,x_n)= \sum_{i=0}^n\theta_ix_i hθ(x0,x1,...,xn)=∑i=0nθixi。进一步用矩阵形式表达更加简洁如下: h θ ( X ) = X θ h_\theta(X)=X\theta hθ(X)=Xθ其中, 假设函数 h θ ( X ) h_\theta(X) hθ(X)为 m × 1 m\times1 m×1的向量, θ θ θ为 n × 1 n\times1 n×1的向量,里面有 n n n个代数法的模型参数。 X X X为 m × n m\times n m×n维的矩阵。 m m m代表样本的个数, n n n代表样本的特征数。
得到了模型,我们需要求出需要的损失函数,一般线性回归我们用均方误差作为损失函数。损失函数的代数法表示如下: J ( θ 0 , θ 1 , . . . , θ n ) = ∑ i = 1 m ( h θ ( x 0 ( i ) , x 1 ( i ) , . . . x n ( i ) ) − y i ) 2 J(\theta_0,\theta_1,...,\theta_n)=\sum_{i=1}^m(h_\theta(x^{(i)}_0,x^{(i)}_1,...x^{(i)}_n)-y_i)^2 J(θ0,θ1,...,θn)=i=1∑m(hθ(x0(i),x1(i),...xn(i))−yi)2进一步用矩阵形式表达损失函数: J ( θ ) = 1 2 ( X θ − Y ) ⊺ ( X θ − Y ) J(\theta)=\dfrac{1}{2}{(X\theta−Y)}^\intercal(X\theta−Y) J(θ)=21(Xθ−Y)⊺(Xθ−Y) Y Y Y是 m × 1 m\times1 m×1维的矩阵,表示输出矩阵,即由 y i ( i = 1 , 2 , . . . , n ) y_i(i=1,2,...,n) yi(i=1,2,...,n)组成的矩阵。由于矩阵法表达比较的简洁,后面我们将统一采用矩阵方式表达模型函数和损失函数。
线性回归算法
对于线性回归的损失函数 J ( θ ) = 1 2 ( X θ − Y ) ⊺ ( X θ − Y ) J(\theta)=\dfrac{1}{2}(X\theta−Y)^\intercal(X\theta−Y) J(θ)=21(Xθ−Y)⊺(Xθ−Y),我们常用的有两种方法来求损失函数最小化时候的 θ \theta θ 参数:一种是梯度下降法,一种是最小二乘法。由于不是本文内容且不影响读者理解线性回归,在此不对梯度下降法和最小二乘法进行详细介绍,若不明白,可以百度,推荐这个网址,梯度下降法,最小二乘法。
如果采用梯度下降法,则 θ \theta θ 的迭代公式是这样的: θ = θ − α X ⊺ ( X θ − Y ) \theta=\theta−\alpha X^\intercal(X\theta−Y) θ=θ−αX⊺(Xθ−Y)通过若干次迭代后,我们可以得到最终的θ的结果。
如果采用最小二乘法,则 θ \theta θ 的结果公式如下: θ = ( X ⊺ X ) − 1 X ⊺ Y \theta=(X^\intercal X)^{−1}X^\intercal Y θ=(X⊺X)−1X⊺Y当然对于求线性回归的系数,还有其他的常用算法,比如牛顿法和拟牛顿法,不是本文重点,这里不详细描述。
多项式回归(线性回归的推广)
回到我们开始的线性模型, h θ ( x 1 , x 2 , . . . , x n ) = θ 0 + θ 1 x 1 + . . . + θ n x n h_θ(x_1,x_2,...,x_n)=θ_0+θ_1x_1+...+θ_nx_n hθ(x1,x2,...,xn)=θ0+θ1x1+...+θnxn, 如果这里不仅仅是 x x x 的一次方,比如增加二次方,那么模型就变成了多项式回归。这里写一个只有两个特征的2次方多项式回归的模型: h θ ( x 1 , x 2 ) = θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 1 2 + θ 4 x 2 2 + θ 5 x 1 x 2 h_θ(x_1,x_2)=θ_0+θ_1x_1+θ_2x_2+θ_3x_1^2+θ_4x_2^2+θ_5x_1x_2 hθ(x1,x2)=θ0+θ1x1+θ2x2+θ3x12+θ4x22+θ5x1x2我们令 x 0 = 1 , x 1 = x 1 , x 2 = x 2 , x 3 = x 1 2 , x 4 = x 2 2 , x 5 = x 1 x 2 x_0=1,x_1=x_1,x_2=x_2,x_3=x_1^2,x_4=x_2^2,x_5=x_1x_2 x0=1,x1=x1,x2=x2,x3=x12,x4=x22,x5=x1x2 ,这样我们就得到了下式: h θ ( x 1 , x 2 ) = θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 3 + θ 4 x 4 + θ 5 x 5 h_θ(x_1,x_2)=θ_0+θ_1x_1+θ_2x_2+θ_3x_3+θ_4x_4+θ_5x_5 hθ(x1,x2)=θ0+θ1x1+θ2x2+θ3x3+θ4x4+θ5x5可以发现,我们又重新回到了线性回归,这是一个五元线性回归,可以用线性回归的方法来完成算法。对于每个二元样本特征 ( x 1 , x 2 ) (x_1,x_2) (x1,x2),我们得到一个五元样本特征 ( 1 , x 1 , x 2 , x 1 2 , x 2 2 , x 1 x 2 ) (1,x_1,x_2,x_1^2,x_2^2,x_1x_2) (1,x1,x2,x12,x22,x1x2),通过这个改进的五元样本特征,我们重新把不是线性回归的函数变回线性回归。
广义线性回归(线性回归的推广)
在上一节的线性回归的推广中,我们对样本特征端做了推广,这里我们对于特征 y y y 做推广。比如我们的输出 Y Y Y 不满足和 X X X 的线性关系,但是 ln Y \ln Y lnY 和 X X X 满足线性关系,模型函数如下: ln Y = X θ \ln Y=X\theta lnY=Xθ这样对与每个样本的输入 y y y,我们用 ln y \ln y lny 去对应, 从而仍然可以用线性回归的算法去处理这个问题。我们把 ln y \ln y lny 一般化,假设这个函数是单调可微函数 g ( . ) g(.) g(.),则一般化的广义线性回归形式是: g ( Y ) = X θ g(Y)=X\theta g(Y)=Xθ 或者 Y = g − 1 ( X θ ) Y=g^{−1}(X\theta) Y=g−1(Xθ)这个函数 g ( . ) g(.) g(.)我们通常称为联系函数, g − 1 ( . ) g^{-1}(.) g−1(.)是 g ( . ) g(.) g(.)的反函数。
岭回归(Ridge回归)
在前面的概述中已经对岭回归(Ridge)和lasso回归的产生背景进行了介绍,本小节将对岭回归的原理进行概述。
线性回归的L2正则化通常称为Ridge回归,它和一般线性回归的区别是在损失函数上增加了一个L2正则化的项,和Lasso回归的区别是Ridge回归的正则化项是L2范数,而Lasso回归的正则化项是L1范数。具体Ridge回归的损失函数表达式如下: J ( θ ) = 1 2 ( X θ − Y ) ⊺ ( X θ − Y ) + 1 2 α ∣ ∣ θ ∣ ∣ 2 2 J(θ)=\dfrac{1}{2}(Xθ−Y)^\intercal(Xθ−Y)+\dfrac{1}{2}\alpha||\theta||_2^2 J(θ)=21(Xθ−Y)⊺(Xθ−Y)+21α∣∣θ∣∣22其中 α \alpha α为常数系数,代表正则化系数,太小就会失去处理过拟合的能力,太大就会因矫正过重而出现欠拟合的现象,需要进行调优。 ∣ ∣ θ ∣ ∣ 2 ||θ||_2 ∣∣θ∣∣2为L2范数。
Ridge回归在不抛弃任何一个特征的情况下,缩小了回归系数,使得模型相对而言比较的稳定,但和Lasso回归比,这会使得模型的特征留的特别多,模型解释性差。至于为什么会这样,在后面的章节中会讲到。
Ridge回归的求解比较简单,一般用最小二乘法。这里给出用最小二乘法的矩阵推导形式,和普通线性回归类似。
令J(θ)的导数为0,得到下式: X ⊺ ( X θ − Y ) + α θ = 0 X^\intercal(Xθ−Y)+\alpha\theta=0 X⊺(Xθ−Y)+αθ=0整理即可得到最后的θ的结果: θ = ( X ⊺ X + α E ) − 1 X ⊺ Y \theta=(X^\intercal X+\alpha E)^{−1}X^\intercal Y θ=(X⊺X+αE)−1X⊺Y其中 E E E为单位矩阵。
针对 α \alpha α的设置,需要单独提一下,python中有可以辅助设置此参数的库RidgeCV,RidgeCV算法与Ridge算法的损失函数与损失函数的优化方法是一致的,只是在验证方法上有所不同。RidgeCV算法对损失函数的常数系数进行了交叉验证,从而自动选择一个合适的系数。在初始化RidgeCV类时候,我们可以传一组备选的值,10个,100个都可以。RidgeCV类会帮我们选择一个合适的系数。
lasso回归
Ridge回归在不抛弃任何一个变量的情况下,缩小了回归系数,使得模型相对而言比较的稳定,但这会使得模型的变量特别多,模型解释性差。有没有折中一点的办法呢?即又可以防止过拟合,同时克服Ridge回归模型变量多的缺点呢?有,这就是下面说的Lasso回归。
Lasso回归有时也叫做线性回归的L1正则化,和Ridge回归的主要区别就是在正则化项,Ridge回归用的是L2正则化,而Lasso回归用的是L1正则化。Lasso回归的损失函数表达式如下: J ( θ ) = 1 2 n ( X θ − Y ) ⊺ ( X θ − Y ) + α ∣ ∣ θ ∣ ∣ 1 J(\theta)=\dfrac{1}{2n}(X\theta−Y)^\intercal(X\theta−Y)+\alpha||\theta||_1 J(θ)=2n1(Xθ−Y)⊺(Xθ−Y)+α∣∣θ∣∣1其中 n n n为样本个数, α \alpha α为常数系数,需要进行调优。 ∣ ∣ θ ∣ ∣ 1 ||\theta||_1 ∣∣θ∣∣1为L1范数。
Lasso回归使得一些系数变小,甚至还是一些绝对值较小的系数直接变为0,因此特别适用于参数数目缩减与参数的选择,因而用来估计稀疏参数的线性模型。
但是Lasso回归有一个很大的问题,导致我们需要把它单独拎出来讲,就是它的损失函数不是连续可导的,由于L1范数用的是绝对值之和,导致损失函数有不可导的点。也就是说,我们的最小二乘法,梯度下降法,牛顿法与拟牛顿法对它统统失效了。此时我们可以通过坐标轴下降法(coordinate descent)和最小角回归法( Least Angle Regression, LARS)来求有这个L1范数的损失函数极小值。
使用坐标轴下降法和最小角回归法进行求解的过程可以参考这个网址
为什么lasso回归容易使得不重要的变量的系数变为0而岭回归却会保留它们
经过上面的介绍,大家已经对岭回归和lasso回归有了基本的认识。不知大家有没有这个疑问,为什么lasso回归容易使得不重要的变量的系数变为0而岭回归却会保留它们呢?本小节将通过图形来解释。
假设线性回归模型中只有两个自变量,系数为 β 1 、 β 2 \beta_1、\beta_2 β1、β2(等同于上文中 θ 1 、 θ 2 \theta_1、\theta_2 θ1、θ2。由于岭回归是在线性回归损失函数中加入了系数的L2正则项,lasso回归是在线性回归损失函数中加入了系数的L1正则项,所以可以得到下图,分别展示了岭回归和lasso回归系数的解,
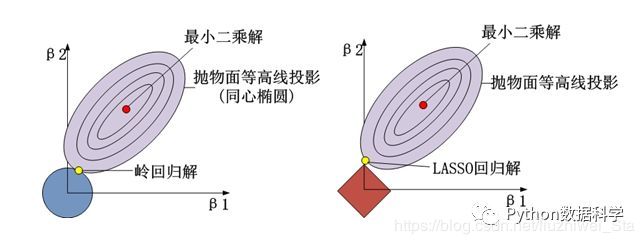
可以清晰地看到:求解的交点不再是最小二乘的最小值(红点),而变成了与正则项的交点(黄点)。这个区别可以从二维图中更好地观察出来:岭回归中两个图形(没有棱角)的交点永远不会落在两个轴上,而LASSO回归中,正则化的几何图形是有棱角的,可以很好的让交点落在某一个轴上。这种稀疏化的不同也导致了LASSO回归可以用于特征选择(让特征权重变为0从而筛选掉特征),而岭回归却不行。
弹性网络(Elastic Net)
介绍完lasso回归和ridge回归,弹性网络就很简单了,损失函数如下: J ( θ ) = 1 2 ( X θ − Y ) ⊺ ( X θ − Y ) + r α ∣ ∣ θ ∣ ∣ 1 + 1 − r 2 α ∣ ∣ θ ∣ ∣ 2 2 J(\theta)=\dfrac{1}{2}(Xθ−Y)^\intercal(Xθ−Y)+r\alpha||\theta||_1+\dfrac{1−r}2\alpha||\theta||_2^2 J(θ)=21(Xθ−Y)⊺(Xθ−Y)+rα∣∣θ∣∣1+21−rα∣∣θ∣∣22使用这种方式方法所得到的模型就像纯粹的Lasso回归一样稀疏,但同时具有与岭回归提供的一样的正则化能力。
弹性网络在很多特征互相联系的情况下是非常有用的。Lasso 很可能只随机考虑这些特征中的一个,而弹性网络更倾向于选择两个,在实践中,Lasso 和 Ridge 之间权衡的一个优势是它允许在循环过程(Under rotate)中继承 Ridge 的稳定性。
结语
本文对线性回归及其相关的延伸进行了基础的介绍,可以帮助大家有一个基本的理解,里面有些细节没有深入展开,若有兴趣,读者可通过更专业的资料进行学习。
参考资料
- https://www.cnblogs.com/yongfuxue/p/9971749.html
- https://blog.csdn.net/lsxxx2011/article/details/98764995
- https://blog.csdn.net/JH_Zhai/article/details/82694937
- https://blog.csdn.net/lsxxx2011/article/details/98764594
- https://www.cnblogs.com/pinard/p/6004041.html
- https://www.cnblogs.com/pinard/p/6018889.html