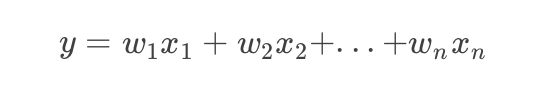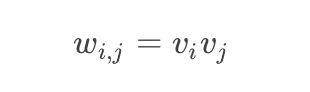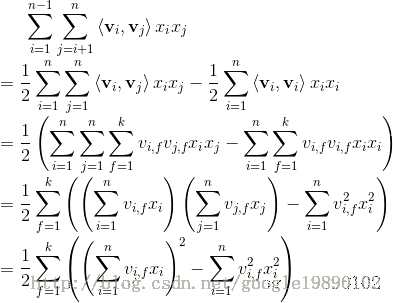1 分解机(Factorization Machines)推荐算法原理
1.1 分解机(Factorization Machines)推荐算法原理
因子分解机(Factorization Machine, FM)是由Steffen Rendle提出的一种基于矩阵分解的机器学习算法。
对于因子分解机FM来说,最大的特点是对于稀疏的数据具有很好的学习能力。现实中稀疏的数据很多,例如作者所举的推荐系统的例子便是一个很直观的具有稀疏特点的例子。
机器学习的通常模式为学习输入到输出的变换,比如最常见的线性回归模型,输入为X,输出为Y,通常输入为高维数据,X是一个向量,形式如下:
线性回归是最简单的线性模型,只能捕捉最简单的一阶线性关系,而且基于各特征独立同分布的假设。
实际中,各特征x1,x2,...xn并不是相互对立的,一般有些特征是相互影响的。此时就需要用多项式回归去建立模型,捕捉这些特征之间的相互影响。
一般为了简单,会只捕捉二阶的关系,即特征间两两相互影响的关系,如下:
这里每两个特征有一个参数w要学习。
这里仍有问题,对于二项式回归来说,如果有n个特征,那么要学习到两两之间的关系,有n(n−1)/2个参数要去学习,对于实际中的复杂任务来说,n的值往往特别大,会造成要学习的参数特别多的问题。
同时,又由于实际数据会有稀疏性问题,有些特征两两同时不为0的情况很少,当一个数据中任何一个特征值为0的时候,那么其他特征与此特征的相互关系将没有办法学习。
受到矩阵分解的启发,为了解决上述两个问题,引入了因子分解机。
如果训练的输入数据有n个特征,设i,j两个特征的相互关系用参数wi,j表示,那么有wij=wji, 这样所有w的参数值会形成一个对称的矩阵,如下:
缺失了对角线的矩阵,正因为如此,我们可以通过给对角线任意设定值来保证矩阵为半正定矩阵,自然想到了矩阵分解。
基于矩阵分解的思想,将以上矩阵分解为两个低阶矩阵的乘积,那么在分解过程中,不仅仅减少了数据存储的复杂度,而且多了一个特别神奇的功能,预测功能。
矩阵分解基于一个假设,即矩阵中的值等于学习到的两个隐向量的乘积,即
这里vi,vj为学习到的隐向量。 那么因子分解机的形式为:
其中,vjf,vif分别为特征i,j对应隐向量的一个隐因子。 通常,由于数据稀疏,本来wij是学习不到的,但是我们可以通过i特征与其他特征的数据,j特征与其他特征的数据,分别学习到i,j特征的参数向量vi,vj,这样wij通过vi,vj的乘积便可以预测wi,j的值,神奇地解决了数据稀疏带来的问题。而且,一般隐向量维度k远远小于特征数量n,那么分解后要学习的参数数量为:n∗k,对比多项式回归的参数数量n(n−1)/2, 从O(n2)减到了kO(n)的级别。
1.2 模型的求解
这里要求出:
求出交叉项。具体过程如下:
1.3 回归和分类
1.4 学习算法
1.4.1 随机梯度下降
关键参数:
- 学习率(太大无法收敛)
- 正则系数(分解机高度依赖正则系数的选择,同时有一种自适应选择正则系数的方法,在libfm中有此实现)
- 初始化值(通常取小值,但不能为0)
1.4.2 交替最小二乘法(Alternating least-squares)
每次选择一个参数,固定其他参数进行优化
相较于梯度下降,没有了超参数学习率
仍有正则系数以及初始化值
1.4.3 马尔科夫链蒙特卡洛法MCMC
属于贝叶斯推断法,采用吉布斯采样,每次优化一个参数。
理论上是最好的方法,因为它首先对超参数的选择不是特别敏感,其次没有了正则系数,也就减少了正则系数的选择时间。同时,超先验参数的个数要小于正则系数的个数,减少了复杂度。
1.5 FM的python实现
#coding:UTF-8
from __future__ import division
from math import exp
import numpy as np
from numpy import *
from random import normalvariate#正太分布
from datetime import datetime
trainData = 'diabetes_train.txt'
testData = 'diabetes_test.txt'
featureNum = 8
max_list = []
min_list = []
def normalize(x_list,max_list,min_list):
norm_list = []
for index,x in enumerate(x_list):
x_max = max_list[index]
x_min = min_list[index]
if x_max == x_min:
x = 1.0
else:
x = round((x-x_min)/(x_max-x_min),4)
norm_list.append(x)
return norm_list
def load_dataset(data):
global max_list
global min_list
dataMat = []
labelMat = []
fr = open(data)#打开文件
for line in fr.readlines():
currLine = line.strip().split(',')
#lineArr = [1.0]
lineArr = []
for i in xrange(featureNum):
lineArr.append(float(currLine[I]))
dataMat.append(lineArr)
labelMat.append(float(currLine[-1]) * 2 - 1)
data_array = np.array(dataMat)
max_list = np.max(data_array,axis=0)
min_list = np.min(data_array,axis=0)
norm_dataMat = []
for row in dataMat:
norm_row = normalize(row,max_list,min_list)
norm_dataMat.append(norm_row)
return norm_dataMat, labelMat
def sigmoid(inx):
# return 1. / (1. + exp(-max(min(inx, 15.), -15.)))
return 1.0 / (1 + exp(-inx))
def stocGradAscent(data_matrix, classLabels, k, iter):
# dataMatrix用的是mat, classLabels是列表
m, n = shape(data_matrix)
alpha = 0.01 # 初始学习率
# 初始化参数
# w = random.randn(n, 1)#其中n是特征的个数
w = zeros((n, 1))
w_0 = 0.
v = normalvariate(0, 0.2) * ones((n, k)) # normalvariate(u, s) 生成均值为u方差为s的呈正太分布的值,ones((n,m))生成n行m列的元素均为1的矩阵;
for it in xrange(iter):
print it
for x in xrange(m): # 随机优化,对每一个样本而言的
inter_1 = data_matrix[x] * v
inter_2 = multiply(data_matrix[x], data_matrix[x]) * multiply(v, v) # multiply对应元素相乘
# 完成交叉项
interaction = sum(multiply(inter_1, inter_1) - inter_2) / 2.
p = w_0 + data_matrix[x] * w + interaction # 计算预测的输出
# print "y: ",p
loss = sigmoid(classLabels[x] * p[0, 0]) - 1
# print "loss: ",loss
w_0 = w_0 - alpha * loss * classLabels[x]
for i in xrange(n):
if data_matrix[x, i] != 0:
w[i, 0] = w[i, 0] - alpha * loss * classLabels[x] * data_matrix[x, I]
for j in xrange(k):
v[i, j] = v[i, j] - alpha * loss * classLabels[x] * (data_matrix[x, i] * inter_1[0, j] - v[i, j] * data_matrix[x, i] * data_matrix[x, I])
return w_0, w, v
# 预测
def predict(x, w_0, w, v):
inter_1 = x * v
inter_2 = multiply(x, x) * multiply(v, v) # multiply对应元素相乘
# 完成交叉项
interaction = sum(multiply(inter_1, inter_1) - inter_2) / 2.
p = w_0 + x * w + interaction # 计算预测的输出
if p < 0.5 :
result = 1.
else:
result = -1.
return result
# 获取正确率
def get_accuracy(data_matrix, classLabels, w_0, w, v):
m, n = shape(data_matrix)
allItem = 0
error = 0
result = []
for x in xrange(m):
allItem += 1
inter_1 = data_matrix[x] * v
inter_2 = multiply(data_matrix[x], data_matrix[x]) * multiply(v, v) # multiply对应元素相乘
#完成交叉项
interaction = sum(multiply(inter_1, inter_1) - inter_2) / 2.
p = w_0 + data_matrix[x] * w + interaction # 计算预测的输出
pre = sigmoid(p[0, 0])
result.append(pre)
if pre < 0.5 and classLabels[x] == 1.0:
error += 1
elif pre >= 0.5 and classLabels[x] == -1.0:
error += 1
else:
continue
print result
return float(error) / allItem
if __name__ == '__main__':
dataTrain, labelTrain = load_dataset(trainData)
dataTest, labelTest = load_dataset(testData)
date_startTrain = datetime.now()
# 训练
print "开始训练"
w_0, w, v = stocGradAscent(mat(dataTrain), labelTrain, k = 20, iter = 200)
# 预测
for line in mat(dataTrain):
print "预测结果为: %f" % (predict(line,w_0, w, v))
print "训练准确性为:%f" % (1 - get_accuracy(mat(dataTrain), labelTrain, w_0, w, v))
date_endTrain = datetime.now()
print "训练时间为:%s" % (date_endTrain - date_startTrain)
# 测试
print "开始测试"
print "测试准确性为:%f" % (1 - get_accuracy(mat(dataTest), labelTest, w_0, w, v))
代码来源及数据集:fm_python
2 FM实现工具libfm
2.1 安装编译libfm
libFM has been tested with the GNU compiler collection and GNU make. Both should be available in Linux and MacOS X.
With the following steps, you can build libFM:
1. Download libFM source code: http://www.libfm.org/libfm-1.42.src.tar.gz
2. Unzip and untar: e.g. tar -xzvf libfm-1.42.src.tar.gz
3. Enter the directory libfm-1.42.src and compile the tools: make all
- 文件概述
• history.txt︰ 版本历史记录和更改
• readme.pdf︰ libfm的手册
• Makefile︰ 使用make编译的可执行文件
• bin︰ executables(需要使用make来build,见1.1节)的文件夹
— — libFM: libFM 工具
— — convert︰ 将文字文件转换成二进制格式的工具
— — transpos︰ 转换二进制设计矩阵的一个工具
• scripts
— — ltriple format to libfm.pl︰ 一个 Perl 脚本将逗号/制表符分隔的数据集 转换成 libFM 格式。
• src︰ 源文件的 libFM 和工具
2.2 数据格式
libFM 支持两种文件格式用于输入数据︰ 文本格式和二进制格式。使用文本格式是更容易的,所以推荐新 libFM 用户使用。
2.2.1 文本格式
数据格式与SVMlite [3] 和 LIBSVM [1] 相同,每一行都都包含一个训练集(x,y),分别提供给实特征向量x和目标y。行首先规定y的值,然后是x的非零值。
对于二进制类型,y>0的类型被认为是积极的一类,y<=0被认为是消极的一类。
4 0:1.5 3:-7.9
2 1:1e-5 3:2
-1 6:1
...
此文件包含三个case:
第一列指出的三个case的每个目标︰4是第一个case的,2是第二的,-1是第三个。
在每个目标之后, 包含非零元素x。如 0:1.5 表示= 1.5 ,3:-7.9 表示= −7.9等等。
即:左边的值是x 的索引,而右边的是 的值,即 = 值。
总之,上述例子表示如下设计矩阵X和目标向量y;
2.2.1.1 转变到推荐文件
在推荐系统中经常使用像 userid, itemid, rating的这样的文件格式。
在script文件夹中的perl脚本是用来将这样格式的数据集转换成libFM的格式的。例如,将Movielens 1M里的rating.csv转换成libFM格式,
使用——
./triple_format_to_libfm.pl-in ratings.dat -target 2 -delete_column 3 -separator "::"
输出将写入到一个文件扩展名为.libfm的文件中。例如,写入toratings.dat.libfm中。
如果一个数据集包含多个文件,如包含训练和测试split,则使用——in后面包含多个文件
./triple_format_to_libfm.pl -in train.txt,test.txt-target 2 -separator "\t"
注意:
如果你为每个文件单独运行一次脚本,则变量(id)将不会匹配了。
例如,第一个文件中的第n个变量将和第二个文件中的第n个变量不一样了。
2.2.2 二进制文件
除了标准的文本格式,libFM 支持二进制数据格式。
该二进制文件的优点:
(1) 读的速度快
(2) 如果您的数据不适合到主内存中,二进制数据格式支持将数据缓存在硬盘并在内存中保留只有一小部分 (使用 — — 高速缓存的大小在 libFM),
(3)如果你使用的 ALS 和 mcmc 方法,你可以预先计算换位的设计矩阵,这可以节省读取数据集时的时间。
使用bin文件夹下的【如下】,可以将LibFM文本格式的文件转换为二进制格式的文件。
./triple_format_to_libfm.pl -in ratings.dat -target 2 -delete_column 3 -separator "::"
例如:
将前面提到的电影数据集转换成二级制格式:
./convert --ifile ratings.dat.libfm --ofilex ratings.x --ofiley ratings.y
输出两个文件:
(1)包含设计矩阵X即预测器变量的文件
(2)包含预测目标y的文件
建议,分别以.x和.y作为文件拓展名
2.2.2.1转置数据(Transpose data)
使用转置设计矩阵(transposed design matrix)来学习MCMC和ALS。
如果您使用的是文本格式,libFm内部会自动转换这些数据。
如果您使用的是二进制格式,二进制格式中必须存在转置数据。
使用transpose工具,将设计矩阵x转换为二进制格式:
例如:转换上述提到的电影数据集:
./transpose --ifile ratings.x --ofile ratings.xt
输出为设计矩阵x的一个转置复制,建议以.xt作为结尾。
2.3 libFm
libFm工具从训练数据集(-train)和验证数据集(-test)中训练FM模型。
libFm有如下选项:
2.3.1 强制参数
• 指定的第一个强制性参数—— -task 要么是分类 (-task c) 要么就是回归 (-任务 r)。
• 第二训练数据 (-train) 和测试数据 (-test) 必须存在。此处可以使用二进制文件,也可以使用libFm文本格式文件。
• 第三,分解机的维度需要用-dim来指定,由三个数字组成,
——来确定全局偏移是否要在模型中使用。
——来确定单向交互(one-way interactions)(为每个变量的偏移)即w是否要在模型中使用
——给出了用于成对相互作用的因素的个数,即k是
例如:一个FM,使用bias,1-way interactions,a factorization of k = 8 forpairwise interactions的回归任务——
/libFM -task r -train ml1m-train.libfm -test ml1m-test.libfm -dim ’1,1,8’
2.3.2 可选参数
2.3.2.1基本参数
• out︰ 训练完毕后,您可以将测试数据集的所有预测结果通过out写入指定的文件。Out-file 是文本格式,与测试数据集的行数相等,第i行的数据为第i个测试数据的结果。
请注意,对于分类,有积极类型的数据输出的是概率。
• rlog︰ 生成一个有关每次迭代的统计信息的日志文件。该文件是 使用制表符分隔字段CSV 格式。
请注意,它取决于哪些字段报道的学习方法。
• verbosity︰ 使用参数-详细级别 1,libFM 打印的详细信息。这是有用的检查是否正确,读取您的数据,并找出错误。
2.3.2.1 高阶参数
Grouping
通过使用meta选项可以进行将输入变量group,grouping可以用来给ALS,MCMC,SGDA来确定更复杂的正则化模型。
每个group可以有一个单独的正则化参数。
为了使用group,元参数需要使用文本文件的文件名,和有很多输入变量和许多行一样。
每一行指定一个相应输入参数的group id。【需要注意的是】group的id需要是从0开始的数字。
例如:
例子1中的设计矩阵(一共7行,最大的id是6)的group文件,应该是这样的
表示的意义是:一共有三组,前两个变量 (设计矩阵中的列)有同组,第三和最后是同一组,第四至第六变量有同一组。
二进制数据和缓存
在2.2.2章节中提到,二进制文件中,设计矩阵以应以.x和目标以.y结尾,转置以.xt结尾。如果在libfm中使用二进制文件,那么不需要以这些格式结尾。
即:如果你有 compiled training (ml1m-train.x, ml1m-train.y,ml1m-train.xt) and 测试数据 (ml1m-test.x, ml1m-test.y, ml1m-test.xt)
使用——
./libFM -task r -trainml1m-train -testml1m-test -dim ’1,1,8’
libFm会自动追加适当的扩展名,并为学习算法载入数据集
如果你的数据不适合进入内存,你可以指定libFM允许多大的文件允许保存在内存中
使用——
./libFM -task r -train ml1m-train -test ml1m-test -dim ’1,1,8’-cache_size 100000000
表示为100,000,000 Bytes (100 MB)的内存可以被.x或者.xt文件使用。
【注意】
.y文件通常完全地读入内存中。
如果没有指定参数cache-size,所有数据将都进入内存。
【注意】
只有当数据因为cache使用比读写内存慢很多的锁(harddisc)的时候而不适合进行内存,才使用caching。
Note: you should usecaching only if the data does not fit into memory because caching uses the harddisc which will be muchslower then memory access.
2.3.3 学习方法
默认的学习方式是MCMC,因为MCMC是非常易于掌握的(没有学习速率,没有正则化项)
在libFM中你可以选择SGD,ALS, MCMC , SGDA。对于所有这些方法,迭代次数(iter)都需要指定
2.3.3.1 Stochastic Gradient Descent (SGD)
通过使用-method sgd参数,可以实现SGD学习方法,对于此方法,以下参数可以选择。
• -learn rate:SGD学习速率的步长,需是一个非零且postive的值
• -regular:正则化参数,需是0或者postive的值
对于SGD,你可以通过以下方法来确定正则化的值:
– One value (-regular value):所有的参数模型使用统一的正则化值
– Three values (-regular ’value0,value1,value2’):0-way interactions (w0) use value0 asregularization,
1-way interactions (w) use value1
pairwise ones (V ) use value2
– No value:使用-regular 0来表示没有指定正则化值
• -init stdev:标准偏差的正态分布,用于初始化V 的参数。在这里你应该使用一个非零的、 postive的值。
请慎重选择这些参数,预测质量很大程度上取决于对很好的选择。
例如:
./libFM -task r -train ml1m-train.libfm -test ml1m-test.libfm -dim ’1,1,8’ -iter 1000-method sgd -learn_rate 0.01 -regular ’0,0,0.01’ -init_stdev 0.1
2.3.3.2 Alternating Least Squares (ALS)
通过使用-method als参数,可以实现SGD学习方法,对于此方法,以下参数可以选择。
• -regular:正则化参数,需是一个非零且postive的值
对于ALS可以使用以下方法来正则化:
– One value (-regular value):所有的参数模型使用统一的正则化值
– Three values (-regular ’value0,value1,value2’):0-way interactions (w0) use value0 asregularization,
1-way interactions (w) use value1
pairwise ones (V ) use value2
– Group specific values (-regular ’value0,value1g1,...,value1gm,value2g1,...,value2gm’):例如,对于m groups如果输入变量是grouped的,对于每个group,
1-way and 2-way interaction 每一个正则化值都被使用,那么有1+2m个正则化值,
– No value:使用-regular 0来表示没有指定正则化值
• -init stdev:标准偏差的正态分布,用于初始化V 的参数。在这里你应该使用一个非零的、 postive的值。
请慎重选择这些参数,预测质量很大程度上取决于对很好的选择。
例如:
./libFM -task r -train ml1m-train.libfm -test ml1m-test.libfm -dim ’1,1,8’ -iter 1000-method als -regular ’0,0,10’ -init_stdev 0.1
2.3.3.3 Markov Chain Monte Carlo (MCMC)
通过使用-method mcmc参数,可以实现MCMC学习方法,对于此方法,以下参数可以选择。
• -init stdev:标准偏差的正态分布,用于初始化V 的参数。在这里你应该使用一个非零的、 postive的值。
请慎重选择这些参数,预测质量很大程度上取决于对很好的选择。
例如:
./libFM -task r -train ml1m-train.libfm -test ml1m-test.libfm -dim ’1,1,8’ -iter 1000-method mcmc -init_stdev 0.1
2.3.3.4 Adaptive SGD (SGDA)
通过使用-method sgda参数,可以实现SGDA学习方法。当采用SGDA时,正则化值(每组和每层)会被自动找到。
你需要去指定一个有效的集合去调优正则化值。
• -validation:包含训练样本的数据集用作验证集合来调优正则化值。此数据集需要与训练数据集区分开。
• -learn rate:学习速率的步长,需是一个非零且postive的值
• -init stdev:标准偏差的正态分布,用于初始化V 的参数。在这里你应该使用一个非零的、 postive的值。
请慎重选择这些参数,预测质量很大程度上取决于对很好的选择。
例如:
./libFM -task r -train ml1m-train.libfm -test ml1m-test.libfm -dim ’1,1,8’ -iter 1000-method sgda -learn_rate 0.01 -init_stdev 0.1 -validation ml1m-val.libfm
2.4.块结构 (BS) 扩展
上图表示:
(a) LibFM 数据文件 (= 的设计矩阵 X 表示形式) 可能包含大块重复的图案。
(b) libFM 的BS 扩展允许使用更紧凑的表示数据文件来表示曾经描述过的重复图案,哪里会只是曾经描述了。(图改编自 [7])
在相关背景下,在设计矩阵可能包含大块的重复的模式 (见图 1a)。 这可能导致设计矩阵非常大,以至于学习速度慢而且占用很多内存。
在libFM的BS扩展中,允许在设计矩阵中定义和利用块结构。BS数据类型取代传统的数据类型所用时间和所占内存都会成线性。
来自相关数据的大的设计矩阵的具体细节详情见[7]
2.4.1数据格式
BS 扩展允许定义块 (例如 B1、 B2、 B3 中图 1),在 libFM 中使用它们。
每个块定义包括︰
• 设计矩阵 (libFM 文件) 的块 (例如 XB1在图 1)。
• 从训练(或测试)case 映射到行中的块 (例如 φ 例B1在图 1)。
• 设计矩阵 中的可选分组(比较第 3.2.2 节) 。对于每个块,预计以下文件︰
2.4.2使用BS数据来启动LibFm
使用--relation参数来传递命令行参数,假设已经定义了两块(rel.user andrel.item)则使用
./libFM -task r -train ml1m-train -test ml1m-test -dim ’1,1,8’ --relation rel.user,rel.item
注意:上面文件中列出的每一块都必须出现。(i.e. rel.user.x, rel.user.xt,rel.user.train, rel.user.test, (rel.user.groups), rel.item.x, rel.item.xt, etc.).
4.3在libFm中使用BS的注意事项
• BS 仅支持由 MCMC 和 ALS/CD。
• 甚至当使用 BS 时, --train ,--test参数是仍旧强制执行,文件必须是在此处指定。LibFM 文件通过--train ,--test可以有预测变量以及但也可能是 空。
文件可以是二进制形式,可以是文本形式
• 在 BS 设计矩阵变量 id 的命名空间是不同的。
• 在BS文件中group的命名空间是不同的。每一个组文件可以有从0开始的组。 – overlaps are resolved the same way as with predictor ids.
• If no group files are passed, each block is automatically assumed to have a different group
Reference:
- 分解机(Fatorization Machines推荐算法原理
- 推荐系统】Factorization Machine
- Factorization Machines in Python实现(没有成功)
- fm_python
- 机器学习算法实现解析——libFM之libFM的训练过程概述
- LibFM使用手册中文版
- FM(因子分解机系列)
- 简单易学的机器学习算法——因子分解机(Factorization Machine)