机器学习第八周 白盒模型-决策树

机器学习第八周 白盒模型—决策树

学习目标

知识点描述：白盒模型——决策树

学习目标：

• 决策树相关概念以及模型算法推导

• ID3、C4.5、CART决策树代码实现

学习内容

决策树1：初识决策树

决策树2: 特征选择中的相关概念

决策树3: 特征选择之寻找最优划分

决策树4：构建算法之ID3、C4.5

决策树5：剪枝与sklearn中的决策树

决策树6：分类与回归树CART

学习ing

白盒模型white box model 决策树：

决策树每个内部节点表示一个测试功能，即类似做出决策的过程，每个叶节点都表示一个标签，即在计算所有特征之后做出的决定。标签和分类表示导致这些类标签的功能的连接。从根到叶的路径表示分类规则。

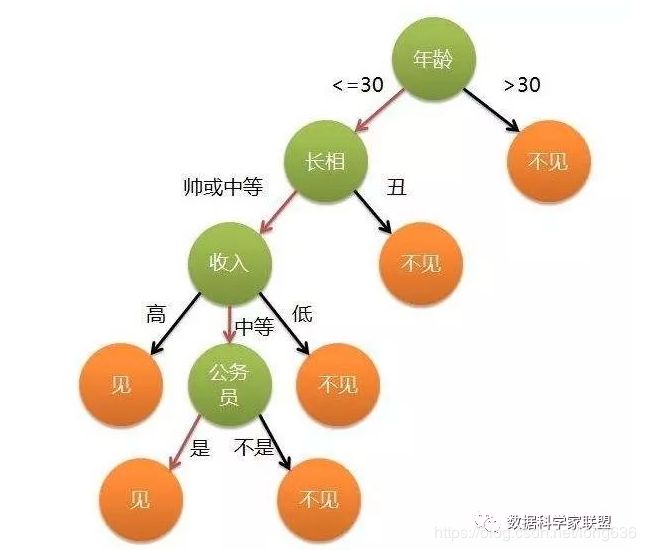
决策树分类思想：从根节点开始，对实例的某个特征进行测试，根据测试结果将实例分配到其子节点，此时每个子节点对应着该特征的一个取值，如此递归的对实例进行测试并分配，直到达到叶节点，最后将实例分到叶节点的类中。

决策树模型：

假设给定的训练数据集
$$D=（x_1,y_1）,(x_2,y_2),(x_3,y_3),...,(x_n,y_n)，其中x_i=(x_i(1),x_i(2),...,x_i(n){)}^T为输入的特征向量，n为特征个数，y_i属于\{1,2,...,K\}为类标记，i=1,2,3,...N,N为样本容量。$$
学习目标是：根据训练样本集构建一个决策模型，能够对它进行正确的分类。同时确保模型能够有较好的泛化能力。

模型优化的函数：这里叫做决策树损失函数，使用正则化的极大似然函数，为什么使用它？暂且不表。先看结果，就是使损失函数最小化。（因为从所有可能的决策树中选取最优决策树是NP问题，NP问题可以理解为在当前算力下会花费无限时间来穷举，因此可以采用启发式算法求近似最优解。NP问题，可以参考《算法导论》）

决策树的构建：特征选择、决策树的生产、决策树的修剪

决策树算法是一个递归选择最优特征的过程，并根据该特征对训练数据进行分割，使得各个子数据集有一个最好的分类的过程。

(1)开始：构建根节点，将所有训练数据都放在根节点，选择一个最优特征，按照这一特征将训练数据集分割成子集，使得各子集有一个在当前条件下最好的分类。

（2）如果这些子集已经能够被基本正确分类，那么构建叶节点，将这些子集分到所对应的叶子节点。

（3）如果子集还不能被正确的分类，那么就对这些子集选择新的最优特征，继续对其进行分割，构建相应的节点，如此递归，直至所有训练数据子集被基本正确分类，或者没有合适的特征为止。

（4）每个子集都被分到叶节点上。

为了获得更好的泛化能力，进行决策树剪枝。

如何进行特征选择，在每个特征上又如何确定分类的阈值？

为了找到最优的划分特征，这里使用不同的损失函数。下面先介绍概念：

信息熵：香农公式，表示信息量的大小。不确定度越大，数值越高。
$$H=-\sum _{i=1}^k{p}_{i}log(p_i)$$
条件熵：数学期望，在随机变量X的条件下随机变量Y发生的不确定性和。
$$H(Y|X)=\sum _{i=1}^n{p}_{i}H(Y|X=x_i)$$
信息增益：在划分数据集前后信息发生的变化成为信息增益。获取信息增益最高的特征就是最好的选择。以某特征划分数据集前后的熵的差值

信息增益率：
$$g_R(D,A)=\frac{g（D,A）}{H_A(D)},分子是特征A对训练数据集D的信息增益，分母是训练数据及D关于特征A的值的熵$$
基尼系数：表示在样本集合中一个随机选中的样本被错分的概率。
$$Gini(P)=\sum _{i=1}^K{p}_k(1-p_k)$$
在找到最优特征后，进行划分（阈值的选取？）

（1）信息熵的最优划分

（2）信息增益最优划分

（3）基尼系数最优划分

在阈值选取后，就进行划分了当前分类，然后递归每个子集。

ID3算法是一种分类预测算法，算法中以信息论中的信息增益为基础，核心是通过计算每个特征信息增益，每次划分选取信息增益最高的属性作为划分标准，递归第构建决策树。没有剪枝过程，只能处理离散分布的数据特征，同时还有一些其他优缺点…

C4.5算法：是对ID3算法的改进，使用信息增益比来选择属性，在决策树的构造过程中对树枝进行剪枝；对非离散数据也能处理，并能够对不完整数据进行处理。

在构建出决策树后，还需要最后一步进行剪枝，目的：降低复杂度，解决过拟合。

剪枝操作：预剪枝 ；后剪枝

CART算法：classification and regression tree.分类树和回归树。既可以解决分类问题，也可以解决回归问题。CART相比较前面两种算法，它采用基尼系数来代替信息增益比，基尼系数代表模型的不纯度，基尼系数越小，不纯度越低，特征越好。