lordofadventure

ACM比赛经验、刷题记录及模板库总结（更新中）

前言

本文所提及的部分题目代码，可以在我的Github上找到

第一部分经验分享及感受

第二部分刷题记录

一、基础算法&程序语言

//strlen()函数的复杂度是O(n)要小心
//截取字符串
strncpy(char* ch,const char* pos,size_t len);
char s[100];
char *p;
strncpy(p,s+10,3);//这个函数不会自动加’\0’

C++ string类

//string反转,需包含头文件
reverse(s.begin(),s.end());

/*
string和int类型互转，需包含头文件和
*/
void str2int(int &int_temp,const string &string_temp)
{
    stringstream stream(string_temp);
    stream>>int_temp;
}

void int2str(const int &int_temp,string &string_temp)
{
        stringstream stream;
        stream<<int_temp;
        //此处也可以用 stream>>string_temp
        string_temp=stream.str();
}

//任意数值类型的模板函数
template <class T>
T stringToNum(string& str)
{
    istringstream iss(str);
    T num;
    iss >> num;
    return num;
}

template<class T>
string numtoString(const T& t){
	//创建一个格式化输出流
    ostringstream oss;
    //把值传递如流中
    oss<<t;
    return oss.str();
}

//读入一行
string s;
getline(cin,s);

//读入直到空格（不包括空格）
string s;
cin>>s;

/*
读入直到指定字符ch，这里ch不会被读入到s中，而且好像也不会存在于缓冲区中
*/
string s;
getline(cin,s,ch);//第3个参数省略时默认为'\n'

//字符串截取
string s;
//注意第2个参数是截取的长度而不是结束的下标
s.substr(s,len);

new&delete

创建并释放一维数组

#include
using namespace std;
int main()
{
    int n;
    cin>>n;
    //分配动态一维数组 
    int *arr=new int[n];
    
    for(int i=0;i<n;i++)
        cin>>arr[i];
    for(int i=0;i<n;i++)
       cout<<arr[i]<<" ";
    //释放arr数组 
    delete[] arr;
    return 0;
}

创建并释放二维数组

#include
using namespace std;
int main()
{
    int row,col;
    cin>>row>>col;
    //为行指针分配空间 
    int **arr=new int *[row];    
    for(int i=0;i<row;i++)
         arr[i]= new int[col];//为每行分配空间（每行中有col个元素） 
    //输入二维数组的数 
    for(int i=0;i<row;i++)
        for(int j=0;j<col;j++) 
        cin>>arr[i][j];
    cout<<"*******************"<<endl;
     //输出二维数组中的数  
    for(int i=0;i<row;i++)
    {
         for(int j=0;j<col;j++) 
          cout<<arr[i][j]<<" ";
        cout<<endl;
    } 
    //释放二维数组（反过来） 
    for(int i=0;i<row;i++)
        delete[] arr[i]; 
    delete[] arr;
    return 0;
}

STL

map

//数据的插入
//示范1
map<int, string> mapStudent;
mapStudent.insert(pair<int, string>(1,“student_one”));/
//示范2
map<int, string> mapStudent;
mapStudent.insert(map<int, string>::value_type (1,“student_one”));
//示范3
map<int, string> mapStudent;
mapStudent[1] = “student_one”;
mapStudent[2] = “student_two”;

map<string, int> mapStudent;
string s;//插入就用m[s]=1或者m[s]++之类;
//数据查找
map<int, string>::iterator iter=mapStudent.find(1);
if(iter != mapStudent.end())
cout<<"Find, the value is "<<iter->second<<endl;
else  cout<<"Do not Find"<<endl;

vector

next_permutation

//自动生成全排列
#include 
#include 
using namespace std;
int main(){
    int n;
    while(scanf("%d",&n)&&n){
        int a[1000];
        for(int i=0;i<n;i++){
            scanf("%d",&a[i]);
        }
        sort(a,a+n);//可以自行测试一下删除后的结果
        do{
            for(int i=0;i<n;i++)
                printf("%d ",a[i]);
            printf("\n");
        }while(next_permutation(a,a+n));
    }
    return 0;
}

优先队列（priority_queue）

struct cmp{
    bool operator()(string &x,string &y){
        return x>y;//从小到大排序
    }
};
priority_queue<string,vector<string>,cmp > q;
//这样的q是将存入的string从小到大

C++11

auto

自动类型推断^【1】

for循环

【代码示例】

#include "stdafx.h"
#include
#include

int main()
{
    std::vector<int> arr;
    arr.push_back(1);
    arr.push_back(2);

    for (auto n : arr)
    {
        std::cout << n << std::endl;
    }

    return 0;
}

断言（assert）

正常使用时assert(表达式);
提交OJ时对于那些不支持assert报RE的（比如说HDU）可以做如下处理
如果原先不是TLE那么头部加入

#define ASSERT(X) if(!(X)) while(true);
#define assert ASSERT

则如果为TLE则说明断言处有误（对于原本提交不是TLE的都有效）
如果原先不是MLE那么头部加入

#define ASSERT(X) if(!(X)){int sz=1;while(sz++){int *num=new int[sz];}}
#define assert ASSERT

如果变成MLE，则说明断言处有误（对于原本提交不是MLE的都有效）
【代码】

#define ASSERT(X) if(!(X)) while(true);
#define ASSERT(X) if(!(X)){int sz=1;while(sz++){int *num=new int[sz];}}
#define assert ASSERT

数据对拍（输入输出重定向-freopen）

【示例代码】

#include 
int main() 
{ 
	int a,b; 
	freopen("D:\\in.txt","r",stdin); //输入重定向，输入数据将从D盘根目录下的in.txt文件中读取 
	freopen("D:\\out.txt","w",stdout); //输出重定向，输出数据将保存在D盘根目录下的out.txt文件中 
	while(scanf("%d %d",&a,&b)!=EOF) 
	printf("%d\n",a+b); 
	fclose(stdin);//关闭重定向输入 
	fclose(stdout);//关闭重定向输出 
	return 0; 
}

【数据对拍模板】

#include 
#define MAXT 1005
#define MAXN 110
#define debug false
const double pi=acos(-1);
const double eps=1e-8;
using namespace std;
struct inputnode{
    int m;
    double R;
    double x[MAXN],y[MAXN],r[MAXN];
};
struct outputnode{
    double myans,ans;
};
struct debugnode{
    inputnode i;
    outputnode o;
}DEBUG[MAXT];
void show_debugnode(debugnode x){
    cout<<x.i.m<<" "<<x.i.R<<endl;
    for(int i=0;i<x.i.m;i++){
        cout<<x.i.x[i]<<" "<<x.i.y[i]<<" "<<x.i.r[i]<<endl;
    }
    cout<<"myans="<<x.o.myans<<endl;
    cout<<"ans="<<x.o.ans<<endl;
    return;
}
int fcmp(double x){
    if(fabs(x)<eps) return 0;
    return x<0?-1:1;
}
int main()
{
    if(debug) freopen("D:\\ACM\\2018MultiTraining\\hdu-5\\data\\1005.in","r",stdin);
    int t;
    scanf("%d",&t);
    for(int casenum=0;casenum<t;casenum++){
        int m;
        double R,ans=0;
        cin>>m>>R;
        if(debug) DEBUG[casenum].i.m=m,DEBUG[casenum].i.R=R;
        ans=2*pi*R;
        for(int debugm=0;debugm<m;debugm++){
            double x,y,r;
            cin>>x>>y>>r;
            if(debug){
				DEBUG[casenum].i.x[debugm]=x;
				DEBUG[casenum].i.y[debugm]=y;
				DEBUG[casenum].i.r[debugm]=r;
			}
       		//程序执行内容
        	if(!debug) printf("%.8lf\n",ans);
       		if(debug) DEBUG[casenum].o.myans=ans;
    }
    if(debug) fclose(stdin);
    if(debug){
        freopen("D:\\ACM\\2018MultiTraining\\hdu-5\\data\\1005.out","r",stdin);
        int t=0;
        while(~scanf("%lf",&DEBUG[t].o.ans)){
            if(fcmp(DEBUG[t].o.ans-DEBUG[t].o.myans)!=0){
                show_debugnode(DEBUG[t]);
                return 0;
            }
            t++;
        }
        cout<<"correct"<<endl;
    }
    if(debug) fclose(stdin);
    return 0;
}

宏定义

带参宏定义^【2】^【3】
#ifdef #define #else #define #endif 可用于代码调试
#define DEBUG
#ifdef DEBUG
#endif
也可用于不同方案的比较
#define solution1
#define solution2
【代码示例】

//下述宏定义可以解决long long报warning问题
#ifdef unix
#define LLD "%lld"
#else
#define LLD "%I64d"
#endif
#define SCANFLL(x) scanf(LLD,&x)
#define PRINTLL(x) printf(LLD,x),printf("\n")
#include

【代码示例】

//一个宏定义模板
#ifdef unix
#define LLD "%lld"
#else
#define LLD "%I64d"
#endif
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#define LL long long
#define maxn 
#define INF 1 << 30
#define rep(i, j, k) for (int i = j; i <= k; i++)
#define For(i, j) for (int i = 1; i <= j; i++)
#define lson l, mid, rt << 1
#define rson mid + 1, r, rt << 1 | 1
using namespace std;
void file() {
	freopen(".in", "r", stdin);
	freopen(".out", "w", stdout);
}

大数模板（C/C++）

JAVA

BigDecimal

可持久化平衡树（C++ Pb_ds库 Rope）

参考文档^【4】
声明
1）头文件
#include
2)调用命名空间
using namespace __gnu_cxx;
底层原理
查了资料，大概可以称作可持久化平衡树，因为rope适用于大量、冗长的串操作，而不适合单个字符操作官方说明如下：
Though ropes can be treated as Containers of characters, and are almost Sequences, this is rarely the most efficient way to accomplish a task. Replacing an individual character in a rope is slow: each character replacement essentially consists of two substring operations followed by two concatenation operations. Ropes primarily target a more functional programming style.Inserting a character in the middle of a 10 megabyte rope should take on the order of 10s of microseconds, even if a copy of the original is kept, e.g. as part of an edit history.It is possible to view a function producing characters as a rope. Thus a piece of a rope may be a 100MByte file, which is read only when that section of the string is examined. Concatenating a string to the end of such a file does not involve reading the file. (Currently the implementation of this facility is incomplete.)
另，根据网上资料，rope本质是封装好的类似块状链表的东东，有人说是logn的，但也有说是n^0.5的。rope不支持一切数值操作，如第k大
小知识
先介绍几个可能使用到的函数
1）append()
string &append(const string &s,int pos,int n);//把字符串s中从pos开始的n个字符连接到当前字符串的结尾或a.append(b);
2）substr()
s.substr(0,5);//获得字符串s中从第零位开始长度为5的字符串（默认时长度为刚好开始位置到结尾）
定义/声明
rope str;
also
r=“abcdefg”
具体内容
总的来说，
1）运算符：rope支持operator += -= + - < ==
2）输入输出：可以用<<运算符由输入输出流读入或输出。
3）长度/大小：调用length()，size()都可以哦
4）插入/添加等：
push_back(x);//在末尾添加x
insert(pos,x);//在pos插入x，自然支持整个char数组的一次插入
erase(pos,x);//从pos开始删除x个
copy(pos,len,x);//从pos开始到pos+len为止用x代替
replace(pos,x);//从pos开始换成x
substr(pos,x);//提取pos开始x个
at(x)/[x];//访问第x个元素
访问
1）迭代器：不说，在竞赛是超时大忌
2）单点访问，直接用数组形式调用下标即可
应用

bzoj1269 文本编辑器

如果想看正常版本的看我的splay平衡树代码
实现操作：
1.（已知）move k：移动光标到目标，初始为0
2.（已知）prev：光标前移一个字符
3.（已知）next：光标后移一个字符
4.insert n s：在光标后插入长度为n的字符串s光标位置不变
5.delete n 删除光标后的n个字符，光标位置不变
6.rotate n 反转光标后的n个字符，光标位置不变
7.get 输出光标后一个字符，光标位置不变
solution
为实现反转操作且保证不超时，我们不调用rope自带的可怕函数，暴力构建两个rope，插入时一个正序插入一个倒序插入，区间即为子串赋值
基本操作

rope test;
test.push_back(x);//在末尾添加x
test.insert(pos,x);//在pos插入x　　
test.erase(pos,x);//从pos开始删除x个
test.copy(pos,len,x);//从pos开始到pos+len为止用x代替
test.replace(pos,x);//从pos开始换成x
test.substr(pos,x);//提取pos开始x个
test.at(x)/[x];//访问第x个元素

其算法复杂度n*(n^0.5)，可以在很短的时间内实现快速的插入、删除和查找字符串，是一个很厉害的神器！
这里有英文版的详解^【5】
【代码】bzoj/1269

牛客网2018暑期多校第3场-C（可持久化平衡树）

【题意】n个数(1-n)，给m个操作，每次操作将当前的一段位置的数拿到最前面，要求输出进行完操作后依次位置的数
【题解】比赛的时候听说是splay树模板题，赛后又听说使用这个rope库（可持久化平衡树）就可以轻松AC
【代码】nowcoder/2018multi/3C

基础题

牛客网2018暑期多校第4场-F-Beautiful Garden-签到题

【题意】
【题解】
【代码】nowcoder/2018multi/4F

枚举

2018ICPC南京站网络预选赛- The writing on the wall

【Source】计蒜客
【TAG】铜牌题枚举
【题解】这题看了网上题解才会做的^【6】，但是实际上写完之后是O(nmm)的复杂度且WA了，对拍了AC程序后修正了BUG，然后就AC了…讲道理是应该TLE的，但是这题数据看来没有那么强。
【代码】jisuanke/2018ICPC/nanjing_pre/The writing on the wall

2018百度之星程序设计大赛资格赛1001-调查问卷

【TAG】状态压缩 bitset 枚举签到题
【题解】问题数只有10个，直接暴力枚举（bitset状压）计算即可，其中我使用到了如下公式
$∏_{1≤i≤j≤n}x_i x_j=\frac 1 2 [(∑^n_{i=1}x_i )^2-∑_{i=1}^nx_i^2]$
来计算不同问卷对数的值，使用左边复杂度为O(n^2)使用右边复杂度为O(n)
【代码】baidustar\2018zigesai\1001

贪心

HDU-6385-rect

【Source】2018百度之星初赛第2场1006
【TAG】贪心
【难度】签到题
【代码】hdu/6385

模拟

2018ICPC南京站网络预选赛-GDY

【Source】计蒜客
【TAG】模拟铜牌题
【题解】
直接模拟即可通过
【代码】jisuanke\2018ICPC\nanjing_pre\GDY

EOJ-3628- A Simple Convolution

【source】2018EOJ8月月赛A
【难度】签到题
【TAG】模拟
【代码】eoj/3628

牛客网2018暑期多校6A-Singing Contest

【TAG】模拟签到题
【题解】贪心选择能击败对手的最小歌曲即可，我用了一个队列，每次2个队首的人出队比较，赢的人入队到队尾。
【代码】nowcoder\2018multi\6A

HDU-6330-Visual Cube-签到题

【题意】给定长宽高，输出立方体模拟图


【题解】2018杭电暑期多校L题签到题；直接找规律输出；每一行计算一下加在前面的点和加在后面的点数。
【代码】hdu/6330

HDU-6342- Expression in Memories-签到题

【题意】给定字符串包含0123456789±？要求把？替换为其他字符，使得其变为合法表达式（不能有前置0），如果无法做到输出IMPOSSIBLE
【TAG】模拟签到题 SpecialJudge
【题解】
不合法情况：
（1）连续2个运算符
（2）前置0
（3）第1个位置和最后1个位置是运算符
问号处：
（1）有前置0的时候放运算符（不能在最后一个位置）
（2）无前置0的时候放‘1’
【代码】hdu/6342

搜索

深度优先搜索（DFS）

HDU-6341-Let Sudoku Rotate

【source】2018杭电暑期多校4J
【难度】比赛铜牌-命题人预估签到
【题意】给定一个从完好数独选定若干个格子进行逆时针旋转若干次后的数独（16*16），要求最小次数还原
【TAG】数独 DFS 最优化减枝可行性减枝
【题解】
要还原就要把一些格子顺时针旋转，由题意一定有解
可以预处理的数据：每个格子最多顺时针0-3次
可行性减枝分析：对于某4行的4个格子，他们的行是否符合数独完全由这一行的4个格子决定，也就是说如果某一种操作使得某4行不符合数独，对其他行再进行操作也不会改变这4行的情况，列也是一样的，以此性质为基础进行可行性减枝。
DFS：依次搜索每一个格子的旋转次数
最优化减枝：当前操作数超过答案是停止搜索
可行性减枝：当前格子旋转这个次数后，使得某一行或某一列已经出现了冲突，那么停止搜索
【代码】hdu/6341

HDU-6351-Beautiful Now

【source】2018杭电暑期多校第5场1002-签到题
【题意】给定一个数字和交换次数，你可以交换数字的某2位，在交换过程中不能出现前导0的情况，问在给定交换次数内可以得到的最小值和最大值是多少
【TAG】搜索贪心
【题解】
998244353 3
理论最小值 233445899
第1次交换 298944353
第2次交换搜索1 238944953
第3次交换搜索1 233944958
第2次交换搜索2 238944359
第3次交换搜索2 233944859
求出理论最大值和理论最小值，把当前数值比照理论值情况，从不符合的位置继续往下贪心的搜索。往下贪心只贪心之后数值最小的位置，搜索是要把这些位置都搜一遍（如果有多个位置的话），直接贪心和最后一个位置换是不对的
比如18900
如果贪心和最后一个换，是10908
对于只要求1次的时候是对的
但是如果要求2次的话，这样贪出来是
18900->10908->10098
而正确的搜索是
18900->10980->10089
【代码】hdu/6351

广度优先搜索（BFS）

二分

HDU-6383-p1m2

【Source】2018百度之星初赛第2场1004
【难度】签到题
【TAG】二分
【代码】hdu/6383

构造

ECNU ICPC/CCPC Trial Round #1-K-Kblack Playing Cards

【题意】给定n张纸牌，每个纸牌上的数字就是说它之后至少有这么多张牌说错了，要求给定一个这些牌的排列，使得恰好有K张牌说错
【题解】关键在于比如一个数字5，如果它在倒数5个位置或更靠后，那么它一定是错的。而一个小的数字如果在前面，则较有可能是对的。假设我们求出了一种排列的情况，满足里面恰好有K张牌是说错了，而其余牌都说对了，那么把已经说错的牌向后移不会改变它的布尔值，把已经说对了的牌向前移也不会改变它的布尔值，因此如果有解，那么一定存在这样的排列，前面都是对的，后面都是错的。并且，如果对的牌都比错的牌要小，且对的牌按照从大到小排序，错的牌按照从小到大排序，即【对大】->【对小】->【错小】->【错大】（对的都比错的小于等于），如果这样都无法满足题意的话，那么可以通过尝试交换任意2个数证明，交换后的结果只可能更远离结果。
【代码】eoj\ICPC CCPC Trial Round#1-K-Kblack Playing Cards

ECNU ICPC/CCPC Trial Round #1-I-Intersections

【题意】给出一个矩形所有中所有数字的相邻关系，要求还原出这个矩阵
【题解】根据每个数有多少数与之相邻（度），然后2就是顶角，3就在边上，4就在里面，依次填上就行了。
【代码】eoj\ICPC CCPC Trial Round#1-I-Intersections

EOJ-3630-Bad Queen

【Source】2018EOJ8月月赛B
【TAG】构造
【难度】签到题
【代码】eoj\3630

HDU-6300-Triangle Partion

【Source】2018杭电暑期多校1
【题意】
【TAG】签到题
【题解】按照x坐标排个序，按顺序输出即可
【代码】hdu\6300

曼哈顿距离最小生成树

参考^【7】

输入输出外挂

参考^【8】^【9】^【10】

题库

2018ICPC南京站网络预选赛-Lpl and Energy-saving Lamps
【Source】计蒜客
【TAG】铜牌题
【题解】
【代码】
铜牌题-前置：无
2018杭电暑期多校7-1011-Swordsman-HDU-6396
【TAG】
铜牌题-前置：无/LCT
2018杭电暑期多校7-1009-Tree-HDU-6394
【TAG】
铜牌题-前置：无
2018杭电暑期多校7-1005- GuGuFishtion-HDU-6390
【TAG】数论欧拉函数
铜牌题-前置：无
2018杭电暑期多校3A-Ascending Rating-HDU6319-铜牌
【题意】
【TAG】单调队列滑动窗口
【题解】
【代码】
铜牌题-前置：无
牛客网2018暑期多校7J-Sudoku Subrectangles
【TAG】
铜牌题-前置：无
牛客网2018暑期多校1D-Two Graphs
【TAG】图匹配搜索
铜牌题-前置：无
牛客网2018暑期多校6I-Team Rocket
【TAG】树状数组线段树区间操作在线处理
铜牌题-前置：无
2018杭电暑期多校第6场1002-bookshelf-HDU6363
(尝试1)铜牌题-前置：无
2018杭电暑期多校4E-HDU6336-Matrix From Arrays
【题意】
【TAG】
【题解】
【代码】
铜牌题-前置：01规划/分数规划
牛客网2018暑期多校5A-gpa
铜牌题-前置：无
牛客网2018暑期多校7C-Bit Compression
【TAG】卡常搜索
（尝试1）铜牌题-前置：无
牛客网2018暑期多校2I-Car
（尝试*1）铜牌题-前置：无
2018杭电暑期多校1B-HDU6299-Balanced Sequence
【题意】
【TAG】
【题解】
【代码】
银牌题-前置：LCA
2018杭电暑期多校7-1008- Traffic Network in Numazu-HDU-6393
【TAG】
银牌题-前置：快速沃尔什变换（FWT）
牛客网2018暑期多校8H-Playing Games
【TAG】博弈论尼姆博弈
（队友AC）铜牌题-前置：无
牛客网2018暑期多校8B-Filling Pools
【TAG】OEIS 找规律
（队友AC）签到题-前置：无
牛客网2018暑期多校8G-Counting regions
【TAG】OEIS 找规律
（队友AC）铜牌题-前置：无
2018杭电暑期多校7-1010-Sequence-HDU-6395
【TAG】矩阵快速幂数论递推
（队友AC）铜牌题-前置：无
牛客网2018暑期多校6C-Generation I
【TAG】排列组合 OEIS
【题解】队友在OEIS上发现了一个很强的规律，即得出的答案在除以m之后，首先n和m交换后的这个值是一样的，其次这个值在OEIS上直接有现成公式，所以就解决了。赛后发现其实是直接推公式也不是太难。
（队友AC）铜牌题-前置：无
2018杭电暑期多校第6场-1009-Werewolf-HDU6370
【TAG】推理图论环基环树
（队友AC）签到题-前置：无
牛客网2018暑期多校7A-Minimum Cost Perfect Matching
【TAG】构造异或
（队友AC）签到题-前置：无
2018杭电暑期多校1D-HDU6301-Distinct Values
【题意】
【TAG】
【题解】
【代码】
（队友AC）签到题-前置：无
牛客网2018暑期多校4D-Another Distinct Values
【题意】
【TAG】数学构造
【题解】
【代码】
（队友AC）签到题-前置：无
牛客网2018暑期多校4G-Maximum Mode
【题意】
【TAG】
【题解】
【代码】
（队友AC）签到题-前置：无
牛客网2018暑期多校6D-Bulbasaur
【TAG】签到题
（队友AC）签到题-前置：无
牛客网2018暑期多校6J-Heritage of skywalkert
【TAG】随机签到题
（队友AC）签到题-前置：无
2018杭电暑期多校1A-HDU6308-Time Zone
【题意】
【TAG】模拟
【题解】
【代码】
（队友AC）签到题-前置：无
2018杭电暑期多校第6场-1012-Pinball-HDU6373
【TAG】物理
银牌题-前置：无
牛客网2018暑期多校2G-transform
【题意】
【TAG】
【题解】
【代码】

二、综合题（现场题）

题库

（队友AC）签到题-前置：无
牛客网2018暑期多校5G-max
（队友AC）签到题-前置：无
牛客网2018暑期多校5J-plan
（队友AC）铜牌题-前置：无
2018杭电暑期多校2E-HDU6313-Hack it
【题意】
【TAG】构造矩阵
【题解】
【代码】
(尝试*1)银牌题-前置：无
2018杭电暑期多校4G-HDU6338-Depth First Search
【题意】
【TAG】深度优先搜索字典序
【题解】
【代码】
银牌题-前置：无
2018杭电暑期多校3M-HDU6331-Walking Plan
【题意】
【TAG】最短路动态规划
【题解】
【代码】
银牌题-前置：无
牛客网2018暑期多校2J-farm
【题意】
【TAG】
【题解】
【代码】
金牌题-前置：无
牛客网2018暑期多校4I-Permutation
【题意】
【TAG】最短路动态规划
【题解】
【代码】

三、动态规划

递推

HDU-2050-折线分割平面

【题意】求解n个折线能把平面分为几个区域
【题解】递推式 $f (n) = f (n - 1) + 4 (n - 1) + 1 = f (n - 1) + 4 n - 3, f (1) = 2$
具体的推导思路大概是考虑前面已经有 $n - 1$ 个折线了，然后现在又来一个折线，看成一个起点的2条射线，这样一交（尽可能往密集了交），按照新的射线大概可以分为3个区域，左射线左增加的区域数，右射线右增加的区域数，两射线之间增加的区域数，左边是 $n - 1$ ，右边是 $n - 1$ ，中间是 $2 (n - 1)$ ，再加1个自带的。反正是看着 $n = 1, n = 2, n = 3$ 的情况连蒙带猜的， $n = 4$ 再网上画也不好画了，这题也没法打表，还没有想到比较严谨的思路。

基础动态规划

最大连续子段和

HDU-1003

【题意】 $n$ 个数求最大连续子段和，同时输出子段的起始终止点（存在多个按照起始点顺序输出第1个，起始点相同的终止点尽可能小）
【题解】最大连续子段和模板题
【代码】hdu/1003

LIS（最长上升子序列）

单调栈优化

HDU-1087

【题意】n个正数，找到一个上升子序列，使得和最大，输出这个最大值，n规模1000
【题解】
$，复杂度 O (n^{2}) 【代码】hdu/1087$

LCIS（最长上升公共子序列）

HDU-1503-Advanced Fruits

【题意】给定2个字符串；要求1个最短的字符串，使得给定的2个字符串都是所求字符串的子序列。Special Judge。字符串长度范围1-100.
【题解】LCIS问题，对于非LCIS的部分，2个字符串的字母都要写。
$d p [i] [j]$ 表示第1个字符串考虑前i个字符，第2个字符串考虑前j个字符时的最大上升公共子序列长度
$s [i] [j]$ 表示考虑第1个字符串前i个字符和第2个字符串前j个字符时的题目所求字符串（也就是最大公共子串，还要加上非公共子串的部分）
当 $a [i] = = b [j]$ 时
$d p [i] [j] = d p [i - 1] [j - 1] + 1, s [i] [j] = s [i - 1] [j - 1] + a [i]$ 或 $b [j]$
当 $a [i]! = b [j]$ 时
$d p [i] [j] = m a x (d p [i - 1] [j], d p [i] [j - 1])$
若选取 $d p [i - 1] [j]$ 则 $s [i] [j] = s [i - 1] [j] + a [i]$
若选取 $d p [i] [j - 1]$ 则 $s [i] [j] = s [i] [j - 1] + b [j]$
初始时 $d p [0] [j]$ 和 $d p [i] [0]$ 均为0
$s [0] [0] = " ", s [0] [j]$ 为b串的前j个字符， $a [i] [0]$ 为 $a$ 串的前i个字符
【代码】hdu/1503

HDU-1159-LCIS模板题

【题意】求最长上升公共子序列
【题解】模板题
【代码】hdu/1159

背包问题

参考^【11】

0-1背包

HDU-2602-Bone Collector

【题意】n个物品，告知n个物品价值、体积，给定背包容量，求解最大存放价值
【题解】0-1背包裸题，题目要求背包不必放满（初始化全0）
【代码】hdu/2602

完全背包

HDU-1114-Piggy Bank

【题意】给定背包容量，n个物品的体积和价值，要求背包刚好装满的最小价值
【题解】完全背包，修改状态转移方程为min，恰好装满，初始化除容量为0之外为非法
【代码】hdu\1114

多重背包

数位DP

HDU-2089-不要62

【题意】求 $[n, m]$ 区间中不含‘4’和‘62’的数字
【题解】数位DP经典入门题，dp[i][j]表示长度为i开头填j这个数字的方案数
$dp[i][j]=\left\{ \begin{aligned} 0 &,&j=4 \\ \sum_{k=0,k\neq2}^9 dp[i-1][k] &,&j=6 \\ \sum_{k=0}^9 dp[i-1][k]&,&j\notin\{4,6\} \end{aligned} \right.$
初始化 $d p [0] [j]$ 为1( $d p [0] [4]$ 为0)
WA了1发之后写了个测试函数，暴力答案对照，随机试了很多组数据都对之后又交了WA了一发，于是写了个遍历n以内所有的对照debug程序，只要有错就跳出来，果然又找到了一些隐藏的错误。
【代码】hdu\2089

状态压缩DP

2018ICPC南京站网络预选赛-AC Challenge

【Source】计蒜客
【TAG】铜牌题状态压缩DP
【题解】
这题的精髓在于位运算中枚举子集与判断是否符合转移条件（即下面代码的注释行）^【12】
【代码】jisuanke\2018ICPC\nanjing_pre\AC Challenge

概率DP

牛客网-第1场-E-Removal-铜牌

【题意】n个数字组成的序列，最多有k种数字（1-k），要求删掉m个数字后，不同的序列个数。数据规模n为，k为10，m为10
【题解】
铜牌题
动态规划 $d p [i] [j]$ 表示长度为i结尾为数字j的方案数， $s u m [i]$ 表示长度为i的方案数。
那么 $s u m [i] = d p [i] [1] + \dots \dots + d p [i] [k]$
$d p [i] [j] = s u m [i - 1]$
答案就是 $s u m [n - m]$
伪代码：
从第1给定序列的第1个数字开始 $C_1...C_n$ ，每次多取1个 $C_i$ {
//考虑前 $i - 1$ 个数字的序列的答案都已经最新
则 $dp[i][C_i]=sum[i-1]$ （同时要首先更新 $s u m [i]$ ）
依次求得 $dp[i-1][C_i]=sum[i-2]......dp[1][C_i]=sum[0]$ （同时更新 $s u m$ 数组）
}
考虑到我们需要的是取到第n个数字时的 $s u m [n - m]$ ，也就是在最后一轮，我们在求dp时，求 $d p [n] [c] \dots \dots$ 到 $d p [n - m] [c]$ 的时候就可以停止了，因为再更新下去也不会改变 $s u m [n - m]$ 的值，这个时候会用到的值就是取第n-1个数字时的 $s u m [n - 1] \dots \dots s u m [n - m - 1]$ ，那么也就是说在取第 $n - 1$ 个数字时，求 $d p [n - 1] [c] \dots \dots$ 到 $d p [n - m - 1] [c]$ 就可以停止了，因为再更新下去也不会影响到我们之后要用的值，以此类推，求第 $i$ 个数字的时候，最多只需要求 $d p [i] [c] \dots \dots$ 到 $d p [i - m] [c]$ 。这样总的时间复杂度就是 $O (n m)$ ,如果内层循环不是只求 $m$ 个就停止的话，那么这样的时间复杂度就是 $O(n^2)$
【代码】nowcoder\2018multi\1E

牛客网-第2场-D-Money-签到题

【题意】n家店，每个店给一个 $p r i c e [i]$ ，可以在一家店以 $p r i c e [i]$ 买入，在另一家店以 $p r i c e [i]$ 卖出，必须按照 $1 - n$ 的顺序访问各家店，起始资金无穷大，同一时刻只能携带 $1$ 个物品，求最大利润和最大利润时的最小交易次数
【题解】 $b u y [i]$ 表示在第I家店进行买入时的最大利润
$buy_op[i]$ 表示在第I家店买入且获得最大利润时的最小交易册数
$s e l l [i]$ 表示在第I家店卖出时的最大利润
$sell_op[i]$ 表示在第I家店卖出且获得最大利润时的最小交易次数
$b u y [i] = m a x (s e l l [0] \dots s e l l [i - 1]) - p r i c e [i]$
当选定某个 $s e l l [k]$ 得到的 $b u y [i]$ 超过原本值时，更新操作数，如果与原来持平，则选取较小的操作数。
$s e l l [i] = m a x (b u y [0] \dots b u y [i - 1]) + p r i c e [i]$
$sell\_op$ 与 $buy\_op$ 类似
可以发现维护4个最值（买入卖出时的最大利润和最小操作数）即可，因为之后的更新只会使用到这些值。
【代码】nowcoder\2018multi\2D

题库

（队友AC）签到题-前置：背包DP
牛客网2018暑期多校3A-PACM Team
【题意】
【TAG】背包
【题解】
【代码】
铜牌题-前置：状压DP
2018杭电暑期多校3C-HDU6321-Dynamic Graph Matching
【题意】
【TAG】状态压缩
【题解】
【代码】
银牌题-前置：数位DP
牛客网2018暑期多校4C-Chiaki Sequence Reloaded
【题意】
【TAG】数学递推式数位DP 找规律
【题解】
【代码】
银牌题-前置：树型DP
牛客网2018暑期多校2H
【题意】
【TAG】树型DP 动态规划
【题解】
【代码】
银牌题-前置：无
2018杭电暑期多校3I-HDU6327-Random Sequence
【题意】
【TAG】GCD 数论
【题解】
【代码】
银牌题-前置：无
牛客网2018暑期多校2B-discount
【题意】
【TAG】
【题解】
【代码】
银牌题-前置：无
牛客网2018暑期多校1B-Symmetric Matrix
【TAG】动态规划图论
HDU-5863-2016多校10-铜牌

四、图论

并查集

图的表示

正向表/前向星

参考^【13】

/*_________________________正向表_______________________________*/
// !!!!!!!!!M=2*M;
//NO.one
int tot,h[M];//标号
struct node{
    int to;//val
    int nx;//must have it pointed the next one
}G[M<<1];
void Add(int a,int b){
    G[++tot].to=b;//val
    G[tot].nx=h[a];//h[]初值为0
    h[a]=tot;
}
for(register int i=h[x];i;i=G[i].nx) //如果为0终止


//NO.two
int A[M],B[M],C[M];//信息
int tot,h[M],nx[M];
void Add(int x,int a,int b,int c){
    //信息 
    A[++tot]=a;
    B[tot]=b;
    C[tot]=c;
    //连接 
    nx[tot]=h[x];
    h[x]=tot;

}
for(register int i=h[x];i;i=nx[i])
    a=A[i],b=B[i],c=C[i];
/*______________________________________________________________*/

最短路

SPFA

HDU-6386-Age of Moyu

【source】2018杭电暑期多校7-1001
【难度】铜牌题
【TAG】最短路 SPFA 前向星
【代码】hdu\6386

51nod-1459-迷宫游戏

【题意】给定n个房间，m条路（2个房间之间只有1条路），到达每个房间有一个正的得分，每条路有一个时间消耗，给定起点、终点，求最短的时间和最短时间下的最大得分
【题解】使用SPFA求解最短路，但是这里最短路的定义（也就是在做松弛操作的时候），以时间消耗越短越好为第一判断，分数得分越大越好为第二判断。
【代码】51nod\1459

UVA-762-We Ship Cheap

【题意】告知若干个点之间连通，求指定起终点之间的最短路径（存在与否、输出路径），连通距离为1
【题解】SPFA模板题（要输出路径，从to逆着找到from，这样可以直接用pre的记录顺着输出），输入没有指定V的个数，但是规定了一定是2个大写字母，所以使用使用哈希思想将其看作是26进制的数表示，直接使用邻接矩阵即可，没有超时
【代码】uva\762

Floyd

UVA-567-Risk

【题意】给定20个城市之间的连通情况，就给定起终点间的最短距离（连通距离为1）
【题解】floyd模板题目，设置100为任意两城市之间的不连通距离，1为直接连通距离
【代码】uva\567

差分约束系统

负环判定

使用SPFA判负环（BFS形式），进入队列超过n次即有负环

POJ-3259-Wormholes

【题意】一张有向图，给定每条边的权值，判断是否有负环
【题解】使用spfa的负环判定，用邻接表可以减少时间复杂度，本题的数据给定的每张图都是连通图，故判定时只要将1作为起始点放入即可，不必再将其他点作为起始点放入，因为但凡是进入过队列的点，都可以认为以其起始过了，所以如果给定的数据不是连通图，则要确保每个点至少进入队列一次
【代码】poj\3259

LCA（最近公共祖先）

2-SAT

图同构

拓补排序

最小生成树

2018百度之星程序设计大赛资格赛-1006-三原色图

【TAG】最小生成树贪心
【题解】分别把2种颜色的边跑一遍最小生成树，跑完记得判有没有连通，比最少的边要少的都是-1，接着把剩下在最小生成树生成过程没有用到的边贪心的从小到大加入即可
【代码】baidustar\2018zigesai\1006

欧拉回路/哈密顿回路

牛客网2018暑期多校8E-Touring Cities

【难度】铜牌题
【TAG】最短路哈密顿回路
【题解】分奇偶讨论即可
【代码】nowcoder\2018multi\8E

树链剖分

线段树优化建图

综合题

HDU-6380-degree

【Source】2018百度之星初赛第2场-1001
【难度】签到
【TAG】连通块
【代码】hdu\6380

题库

铜牌题-前置：拓补排序/线段树优化建图
牛客网2018暑期多校4J-Hash Function
【题意】给定哈希函数和最后的结果，逆推出加入数字的过程（优先字典序小的）
【TAG】拓补排序哈希函数
【题解】
【代码】
银牌题-前置：欧拉回路
2018杭电暑期多校2C-HDU6311-Cover
【题意】
【TAG】欧拉回路
【题解】
【代码】
金牌题-前置：最小生成树/Boruvka算法
2018杭电暑期多校3K-HDU6329-Transport Construction
【题意】
【TAG】
【题解】
【代码】

五、字符串算法

KMP

这个视频讲的很详细…比较容易懂^【】

HDU-1711-Number Sequence

【题意】给定数字序列a和b，如果b序列是a序列的子序列，输出其在a序列中第1个出现的位置（下标从1开始），否则输出-1。
【题解】KMP模板题，在交之前写了个随机化测试以验证程序是否正确。
【代码】hdu\1711

HDU-1686-Oulipo

【题意】求b字符串在a字符串中的出现次数，字符为大写字母，长度范围1e6
【题解】KMP简单题，发现之前做过一次，将b字符串末尾添加1个不可能被匹配到的字符（如’#’），正常求next数组，在作匹配时b字符串只要’#’之前的字符都被匹配就计数1次，继续匹配，而不return；在提交前通过了随机测试
【代码】hdu\1686

HDU-2087-剪花布条

【题意】给定字符串a和b，问a最多能拆出多少个b字符串
【题解】KMP简单题。a中可能有多种选择方案，按顺序从前往后匹配一定是数量最多的。考虑这样证明。假定我们已经在a中选择了n个不想交的b串b1,b2…bn（从前往后）。对于某一个串，如果同时有2个串与它相交（不可能有3个或以上的串与它相交还保持互不相交），且替换为这2个串之后n+1个串都互不相交，则应该作出这样的替换，这种情况被替换的串一定在替换后的（更优解的中间），因此如果按照顺序选取就一定会先选到更优解而不是这个应该被替换的串。
【代码】hdu\2087

循环节问题

HDU-3746-Cyclic Nacklace

【题意】给定1个字符串（长度范围1e5），要求在左侧或右侧补上最少的字符，使得它的循环节数量超过1.
【题解】首先对于这个问题，在左侧补和在右侧补是一样的（包括在两侧同时补），因为假定我们在一个字符串s的左侧补上了 $a$ 个字符，右侧补上了 $b$ 个字符，此时它成为了一个循环串，由循环串的性质，当我们把左侧 $a$ 个字符顺次添加到右侧时，不改变它的循环性质。因此我们只需要考虑添加字符在右侧的情形。
考虑1个字符串 $s$ 和它自身按如下方式进行匹配。（不含完全覆盖本身的情况）
$aaaassssssssss\\ \,\;\;\;\;\;\;\;ssssssssssbbbb$
设j为公共部分的最大长度.
考虑前面的串 $a a a a$ 和后面的串 $b b b b$
如果他们是一样的话，那么 $s$ 就是一个循环串，并且 $l e n (s) - j$ 或者说 $a$ 或 $b$ 串的长度就是其最小循环节长度.
证明的思路如下
$|aaaa|ssssssssss\\ \;\;\;\;\;\;\;\;\;\,ssssssssss|aaaa|$
推出
$|aaaa|aaaa|ssssss\\ \;\;\;\;\;\;\;\;\,|aaaa|ssssss|aaaa|$
以此类推，证明当中的长度恰好被 $l e n (s) - j$ 还没有想好
当 $a$ 串和 $b$ 串不相等时, $l e n (s) - j$ 就是s串通过增加最少字符成为循环串后的循环节大小
也可以类似上面的方式理解。
设 $u n i t = l e n (s) - j$ 表示循环节大小
可以证明加上 $unit-len\%unit$ 个字符后可以变成循环节大小为 $u n i t$ 的循环串。
不过要严格证明其为最小的话还要反证出更小的不可能。
【代码】hdu\3746

HDU-1358-Period

【题意】给定字符串s（长度范围1e6），求它所有前缀是否是循环串，如果是，输出循环节组数
【题解】KMP循环节问题的经典结论题。在HDU3746的基础上对时间复杂度有了更高要求，在求一个串是否为循环串时，我们之前用了自己匹配自己后，前后多出来的部分是否相同来判断是否为循环串。
$aaaaassssssssssss\\ \;\;\;\;\;\;\;\;\;\,ssssssssssssbbbbb$
这里实际上并不需要判断，只要看循环节长度（假定的）是否整除串的长度，如果是的话，那么前后的 $a$ 串和 $b$ 串一定会相同，否则就一定不相同。而且也不用再拿一个自己来匹配了，直接使用next数组即可，因为这个自己和自己匹配的过程本身就是在求next数组，对于 $0, \dots, i - 1$ ，到第 $i - 1$ 个字符时，总共有 $i$ 个字符，考虑 $n e x t [i - 1]$ 的含义就是如果下一个字符不匹配的话，就要跳到 $n e x t [i - 1]$ ，也就是说， $n e x t [i - 1]$ 是前i个字符的最大前后缀相同长度，也就是我们上图中s串的大小，那么循环节长度就是 $i - n e x t [i - 1]$ ，不过要排除一个 $n e x t [i - 1]$ 等于0的情况，其实广义上说这种情况也是满足循环节的，只不过循环次数是1，而题目中一般要求循环次数要大于1，所以要特判一下下。
【代码】hdu\1358

POJ-2406-Power Strings

【题意】给定字符串，求最大循环次数
【题解】铁铜题难度；利用len-next[len-1]求出最小循环节长度，判断一下是否整除len即可。学了一下如何用new，果然直接开1e6本地codeblocks会爆栈，用了new之后就不会了。
【代码】poj\2406

牛客网2018暑期多校3E-Sort String-铜牌题

【TAG】KMP 字符串循环节
【代码】nowcoder\2018multi\3E

HDU-2203-亲和串

【题意】给定字符串a和b判断b是否为a在经过任意次循环移位后的子串
【题解】处理序列循环移位的惯用套路-写2遍，这样的一个新的序列一定包含了所有的循环移位序列，之后就变成KMP模板题
【代码】hdu\2203

POJ-2752-Seek the Name,Seek the Fame

【题意】给定字符串 $s$ （长度范围 $4 e 5$ ）要求输出所有的前缀和后缀相同的字符串长度（升序）
【题解】考虑KMP的 $n e x t$ 数组本质，对于长度为 $l e n$ 的字符串 $0 . . l e n - 1$ ， $n e x t [l e n - 1]$ 的意思就是它（除自己本身）的最大前后缀相同的长度是 $n e x t [l e n - 1]$ ，接着我们就只考虑这个相同的前后缀，再看除它自己本身之外的最大前后缀相同的长度，这样就是 $n e x t [n e x t [l e n - 1] - 1] \dots$ 依次类推可以求出所有的前后缀相同数值。复杂度 $O (n)$
【代码】poj\2752

最长公共子串问题

时间复杂度 $O(n^2)$

POJ-3080-Blue Jeans

【题意】给定至多10个长度为60的字符串，输出它们的最长公共子串（优先输出字典序最小的）
【TAG】最长公共子串 KMP 枚举铁铜题
【题解】求2个字符串的最长公共子串的时间复杂度已知的最好的是 $O(n^2)$ ，所以这题一开始就是一个比较暴力的思路，开始想着是先求第1个和第2个最长公共子串（枚举第1个子串的开始，然后用KMP），再求前2个最长公共子串和第3个…依次类推，这样的时间复杂度应该也说的过去，写到一半发现1个问题，就是如果第1个和第2个最长公共子串有2个及以上，那要保留哪一个呢…也许保留某一个和之后求出来的会更大，这样事情一下子变得棘手了起来。正解是直接暴力枚举第1个字符串的所有子串（也就是1+2+…+60这么多种），从长到短依次与其余的字符串进行KMP匹配，如果在当前长度找到了，就不再找了，但是当前长度必须要全部求完，因为如果发现字典序更小的那么要更新答案。
时间复杂度大约 $O (1 e 6)$
【代码】poj\3080

HDU-1238-Substrings

【题意】n个字符串，找一个字符串，这个字符串或是它的反转是这n个字符串的子串
【TAG】字符串枚举 KMP 签到题
【题解】和POJ3080是一个套路，暴力枚举即可，每次匹配的时候正反都匹配一下。严格按照数据规模要 $10^8$ ，不过这题看来数据没有那么强。
【代码】hdu\1238

HDU-2328-Corporate Identity

【题意】给定n个字符串，求它们的最长公共子串（优先输出字典序小的）
【TAG】字符串最长公共子串枚举 KMP 签到题
【题解】POJ3080原题，改了一下输入输出就过了
【代码】hdu\2328

HDU-2594-Simpsons’Hidden Talents

【题意】给定2个字符串a,b要求最长的字符串s，s是a的前缀同时是b的后缀
【TAG】字符串 KMP 前缀后缀签到题
【题解】一开始以为是扩展KMP，吓得去学习了一波。学完之后发现扩展KMP解决的是字符串a和b，a的所有后缀中与b的最长公共前缀。而本题要求的是b的后缀与a的一段前缀相同，即扩展KMP中的后缀的公共前缀不要求一直通到尾部，而本题是要一直通到尾部的。所以实际上就是把a串作为模式串与b串进行匹配，匹配结束时，a串被匹配了多少就是答案。我们之所以只需要考虑匹配结束时模式串被匹配了多少，是因为如果一个匹配就算再长（哪怕匹配完了）也不是我们关心的答案，比如abcde去匹配abcdeabc，本题要的答案是abc而不是当中的abcde
【代码】hdu\2594

HDU-4300-Clairewd’s message

【题意】给定26个字母的明密文转换表，在给定一个字符串s，这个字符串s一定是由密文+明文的文本的一个前缀，要求最短的可能完整的文本
【TAG】字符串密码 KMP 签到题
【题解】要文本最短的情况就是前一半刚好是密文，后一半刚好是对应的明文，如果是偶数的时候都不用再补了，不管怎么说前一半一定都是密文，所以直接先翻译为明文，和剩下的文本进行KMP匹配，匹配结束时j的值（也就是前一半被匹配的数量），就是已经出现的明文的最大可能长度，那么把剩下的明文补上就可以了。这题要注意的地方，第一个是密文是长度/2向上取整（比如说5个是要取3个），另外最后再输出的时候一定要搞清楚补上的是明文，补明文的时候确保是从密文翻译过来了，因为一开始只翻译了前一半的密文，所以后面可能会遗漏一些密文还没有翻译。
【代码】hdu\4300

最小最大表示法

令 $i = 0, j = 1$
如果 $S [i] > S [j] i = j, j = i + 1$
如果 $S [i] < S [j]$ ,则 $j + +$
如果 $S [i] = = S [j]$ 设指针 $k$ ，分别从 $i$ 和 $j$ 位置向下比较，直到 $\neq S[j+k]$
如果 $S [i + k] > S [j + k]$ ，则 $i = i + k$ 否则 $j$ ++
返回 $i$ 和 $j$ 的小者

int minimalRepresentation() { 
int n = strlen(str); 
int i = 0,j = 1, k = 0; 
while(i<n && j<n && k<n) { 
int t = str[(i+k)%n] - str[(j+k)%n] ; 
if(t == 0) k++; 
else { 
if(t>0) i+=k+1; 
else j+=k+1; 
if(i==j) j++; k = 0; 
} 
} 
return i < j ? i : j; 
}

扩展KMP

最长回文子串（Manacher算法）

字典树

AC自动机

后缀数组

回文树-前置：后缀数组

参考^【15】

题库

金牌题-前置：无
牛客网2018暑期多校2K-Carpet
【题意】
【TAG】KMP
【题解】
【代码】
金牌题-前置：无
牛客网2018暑期多校1I-Substrings
【TAG】字符串同构

六、数据结构

参考^【16】

前缀和

2018百度之星程序设计大赛资格赛-1002-子串查询

【TAG】前缀和字符串字典序签到题
【题解】最小字典序的子串一定只有一个字符，维护26个字母的前缀和数量即可
【代码】baidustar\2018zigesai\1002

线段树

线段树：区间更新

ICPC徐州站网络预选赛-Trace

【Source】计蒜客
【TAG】线段树历史最值
【代码】jisuanke\2018ICPC\xuzhou_pre\Trace

ICPC徐州站网络预选赛- Ryuji doesn’t want to study

【Source】计蒜客
【TAG】线段树签到题
【题解】
它要查询的是 $a [l] * L + a [l + 1] * (L - 1) + \dots + a [r]$
也就是
$(a [l] + a [l + 1] + \dots + a [r]) + (a [l] + a [l + 1] + \dots a [r - 1]) + \dots + (a [l] + a [l + 1]) + a [l]$
维护一个后缀和数组 $p o s t a [i]$
上式即为
$(posta[l]-posta[r+1])+(posta[l]-posta[r])+…+(posta[l]-posta[l+1])\\ =L*posta[l]-(posta[l+1]+…+posta[r+1])$
可见线段树中维护后缀和数组，每次查询就是 $l o g$ 级别
每次更新就是区间更新 $[1, p o s]$ 也是 $l o g$ 级别
【代码】jisuanke\2018ICPC\xuzhou_pre\Ryuji doesn’t want to study

HDU-6315-多校2铜牌题

【题意】 $b$ 数组是 $1 - n$ 的一个排列， $a$ 数组开始全0，更新操作为将一段区间的 $a$ 数组都加1，查询操作为查询一段区间的 $\sum \lfloor \frac {a_i} {b_i}\rfloor$
【题解】每个区间维护差几加几（差left加add）
【代码】hdu\6315

HDU-6356-Glad Your Came

【source】2018杭电暑期多校第5场1007-铜牌题
【题意】数组大小 $n$ （从1开始），初始全为0，给定生成函数和初始值，每次生成 $l, r, v$ ，总共生成 $m$ 次，将 $[l, r]$ 中比 $v$ 小的都更新为 $v$ ，最后求 $\oplus_{i=1}^n i\cdot a_i$
【TAG】线段树异或和区间更新区间查询
【题解】线段树节点记录当前区间的最小值，开始的时候只更新区间的最小值，不更新和，最后一次性查询和。这个写完之后会TLE，加一个减枝就过了。就是更新的num如果比当前区间的最小值更小了，那么就直接减枝掉。开始的uint32_t搞了半天，不过只要样例对了基本就没问题了。
2的30次方可以直接用1<<30，不用快速幂了
官方题解中的做法是一种类似ST表的操作。
【代码】hdu\6356

线段树：区间合并

POJ-3667-Hotel（线段树区间合并模板题）

【题意】
n个房间，初始时均为空，2种操作，第1种操作是找到指定的k个连续空房间，如果找得到的话输出第1个房间号，否则输出0，优先找房间号小的，第2种操作是指定连续的x号到y号房间清空。数据规模n为50000.
【代码】poj\3667

离散化&扫描线

HDU-1542-Atlantis（矩形面积并）

【题意】
给定n个矩形（题目给出每个矩形的左下和右上点坐标，浮点数，坐标范围0-100000，最多100个），求面积并
【题解】
选定横坐标离散化（这样最多100*2个），自下而上扫描，碰到下面的边就把离散化后的相应区间+1，碰到上面的边就-1，从0到1时当前横坐标和增加该离散化区间的原始长度，从1到0则是减少。
【代码】hdu\1542

HDU-5862-2016多校10-铜牌

【题意】给定n个与坐标轴平行的线段（以端点坐标给出），求解交点个数，n的规模为 $10^5$ ，坐标的原始规模为 $10^9,10^9]$
【题解】首先离散化，使得坐标规模缩小到 $10^5$ ，接着使用扫描线，一开始用了错误的算法，本想以 $up\_num[y]$ 表示在y以上的那些以竖线上端点在y以上的个数， $down\_num[y]$ 表示竖线下端点在y以下的个数，这样2者相加就是完全在上+2*相交+完全在下，再减去整体的数量，就可以得到相交到的数量，但是这里由于是线段，所以要求的上述数量都是在一个范围的，总体数量还可以用线段树在 $nlog_2n$ 级别解决，但是在上和在下就涉及到二维线段树，时间复杂度无法降低。
正确算法是采用扫描线，自上而下扫描，对于同一纵坐标，先处理竖直线上端点，单点更新线段树+1，再处理水平线，区间查询增加ans值，再处理竖直线下端点，单点更新-1。
另外这里线段树可以不用建树，只需维护 $c n t$ 即可，可以节省一些时间和空间的复杂度。
要注意最后的 $a n s$ 是会爆int的，水平线和竖直线各 $\frac n 2$ 完全相交的情况可以达到 $\frac {n^2} 4$ 。
HDU上提交的时候选用C++编译器会TLE，选用G++编译器可AC
【代码】hdu\5862

二维线段树

综合题

2018百度之星程序设计大赛资格赛-1005-序列计数

【TAG】LIS DP 树状数组线段树前缀和随机
【题解】设 $d p [i] [k]$ 表示以第 $i$ 个数字结尾，长度为 $k$ 的上升子序列个数。
$ans[k]=\sum_{i=1}^{len}dp[i][k]$
$dp[i][k]=\left\{ \begin{aligned} 1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; &,&k=1 \\ \sum_{jdp[i][k]=⎩⎪⎨⎪⎧1j<i,num[j]<num[i]∑dp[j][k−1],,k=1k=1$

牛客网2018暑期多校5F-take

【题意】给定 $n$ 个盒子（数据规模 $1 e 5$ ），每个盒子有一个概率 $p$ 出现大小为 $d$ 的宝石（或者不出现任何东西），主人公开始的宝石大小为 $0$ ，从 $1$ 到 $n$ 顺次打开每个盒子，如果里面的宝石比手上的大就进行交换，求交换次数的期望值。（输出答案取模 $998244353$ ）
【TAG】概率期望前缀积树状数组线段树逆元
【题解】
设随机变量 $X_1,X_2,...,X_n$
其中 $X_i=\left\{ \begin{aligned} 0 &\;\;打开第i个盒子后不交换& \\ 1 &\;\;打开第i个盒子后交换& \end{aligned} \right.$
题目所求即为 $E(\sum_{i=1}^nX_i)$
根据期望的可加性（线性性）进行事件分解（注意这个性质对独立性没有要求）
$E(\sum_{i=1}^nX_i)=\sum_{i=1}^nE(X_i)$
因此我们主要关心 $E(X_i)$ 的求解
$E(X_i)=0\times P(X_i=0)+1\times P(X_i=1)=P(X_i=1)$
即第 $i$ 个盒子的期望交换次数等于打开第 $i$ 个盒子后交换的概率
打开第 $i$ 个盒子后会发生交换的情况是，第 $i$ 个盒子开出宝石，并且前 $i - 1$ 个盒子中那些潜在拥有比这个宝石大的盒子不能开出宝石。即：
$P(X_i=1)=Box[i].p \prod_{Box[k].size\geq Box[i].size}1-Box[k].p$
暴力求解复杂度不能接受，需要维护比当前盒子都要大的盒子的概率乘积（ $1 - p$ 的乘积）考虑将盒子大小从大到小排序，记录1个 $r a n k$ 值，开始的时候将维护的数组 $d$ 全部赋值1，当按照1到 $n$ 的顺序访问盒子的时候，比如访问到了第i个盒子，那么找到这个盒子的 $r a n k$ 值，那么在 $d$ 数组中所有比这个 $r a n k$ 值低的位置就是存放着那些比它大的盒子的概率，如果一个盒子还没有被访问过，那么里面存着1，不影响乘积结果，在计算完第i个盒子移到下一个盒子之前，把第 $i$ 个盒子的 $1 - b o x [i] . p$ 存入 $d$ 数组相应的 $r a n k$ 位置。这就是一个前缀积的问题，想要快速查询前缀积就是用树状数组或者线段树即可。
注意到题目中给定的 $p$ 值是乘了100的，所以在使用的时候需要除100再用，即乘上100的逆元。（ $998244353$ 显然是素数）。
看了别人的代码之后发现我的代码还可以再优化。那个前缀积的数组可以直接按照次序存，然后计算的时候按照从大到小的顺序来算，这样可以少排序一次，这样的话，每个盒子在计算的时候只会用到比它次序小的盒子的值，这样一个次序比它大的盒子先更新对它没有影响，只要确保一个盒子在计算的时候，所有比它次序小且比它大的盒子都更新过了，所以按照从大到小来更新就是对的。
【代码-树状数组版本】nowcoder\2018multi\5F

牛客网2018暑期多校1J-Different Integers

【题意】给定 $n$ 个数， $m$ 个查询，每次查询 $i, j$ 要求 $[1, i]$ 和 $[j, n]$ 这2个区间内有多少不同的数字。
【TAG】区间查询离线操作单点更新线段树树状数组
【题解】这道题在比赛期间可能可以用莫队算法苟过去，赛后加强数据之后会T，详见莫队算法中的描述。这里是采用了官方正解。
考虑一段区间内出现了多少种数字和考虑一段区间内没有出现多少种数字是一样的。
当我们调整一段区间的端点导致数字出现种数发生变化的实质是触碰到了2个值，某一个数字第1次出现的位置和某一个数字最后一次出现的位置。现在对于区间查询我们显然应该采用离线操作，于是可以固定一个端点使之单调增加，不妨使得右端点r单调增加。对于某一个数字 $x$ ，当 $r > l a s t [x]$ 时，我们根本不关心左端点的左侧是否出现过 $x$ ，因为右端点右侧一定有 $x$ ,而当我们移动右端点到 $r = l a s t [x]$ ，再往右移时，对于 $x$ 是否出现我们就会关心 $x$ 是否在左端点的左侧出现，当 $l > = f i r s t [x]$ 时， $x$ 在左端点的左侧出现，而当 $l < f i r s t [ x ] l时， x x 就没有出现了（既不在左端点左侧也不在右端点右侧）。对于某一个特定的 r r ，我们就关心在 [ l + 1 , r − 1 ] [l+1,r-1] 这个区间内有多少位置是 f i r s t [ x ] first[x] 所在的位置，我们只是需要统计那些 l a s t [ x ] last[x] 已经被 r r 超过了的 x x ，统计出了这个值之后我们拿总数减去这个值就是答案。我们的操作是这样的， r r 先放在最左边，这时候所有的数都被包含在内，我们用一个数组 d d 维护我们需要的值，开始数组 d d 清0，现在我们的r往右移动，移动到某一个值 r = = l a s t [ n u m [ r ] ] ] r==last[num[r]]] ，即在 r r 这个位置出现的数字是它最后一个出现了，那么这时候开始我们就开始关心这个数 n u m [ r ] num[r] 在左侧的命运了，以前我们并不关心它，因为它一定出现，这时候我们就要找到这个数第1次出现的位置 f i r s t [ n u m [ r ] ] first[num[r]] ，将 d [ f i r s t [ n u m [ r ] ] ] ] d[first[num[r]]]] 设置为1，这意味着，当 l l 在 f i r s t [ n u m [ r ] ] first[num[r]] 左侧的时候，这个数字就不在我们的范围里了，所以我们只要统计 [ l + 1 , r − 1 ] [l+1,r-1] 内 d d 数组的和，我们就知道有多少数字不在我们的范围里了。这里我们用线段树维护区间和。【代码-线段树版本】nowcoder\2018multi\1J$

HDU-5861-2016多校10-铜牌

【题干】
一条直线上 $n$ 个村庄， $n - 1$ 个道路，每个道路有一个每天开放的费用。开始的时候所有道路关闭，现在已知 $m$ 天的通行计划，每天给出 $a$ 和 $b$ ，要求a到b之间的道路开放，每个道路只能开放和关闭一次，要求总费用最小。
样例输入为4个村庄，3天计划，道路费用1,2,3，接下来3天计划
【题解】
$200000$ 的数据规模，想知道一个道路最早被使用的时间和最晚被使用的时间（如果被使用到的话），那么道路在此之前和之后都是关闭的，这样是最小的费用，假设我们知道了每个道路的最早和最晚使用时间，那么扫一遍时间，每天加上开放的，减去关闭的，这样输出费用复杂度为 $O (3 m)$ （每个道路最多出现2次）；它每次给出信息对一段区间进行操作，使用线段树，维护每个从开始到结束时每个节点得到的最大值和最小值（注意这里的最大值最小值不是区间的最大值和最小值，而是整个历史记录的最大值和最小值）
【代码】hdu\5861

树状数组

解决动态前缀和查询
单点修改/区间查询
区间加/单点查询
二维树状数组
题库
POJ-2352 二维偏序问题
BZOJ-1878
BZOJ-2743
BZOJ-1452
Codeforces-755D-PolandBall and Polygon

单调队列&单调栈

题库
单调队列
HDU 3415
HDU 3530
POJ 2796
单调栈
HDU 1506
HDU 5033
PKU 2796
PKU 3250

莫队算法

参考^【18】^【19】
适用于可以进行离线操作的区间询问，核心思想是分块。
时间复杂度 $O(m^{1.5})$
将 $m$ 个询问分成 $\sqrt m$ 块，先按照 $l$ 从左到右排序，每个块内再按照 $r$ 从左到右排序。
然后依次处理查询。
对于一道特定题目，应用莫队算法在于搞清楚如何快速（ $O (1)$ 复杂度）算出 $[l, r]$ 到 $[l, r + 1], [l, r - 1], [l - 1, r], [l + 1, r]$
另外一个相关的算法是曼哈顿距离最小生成树，时间复杂度 $O(mlog_2m)$ 这里 $m$ 是询问次数

牛客网2018暑期多校第1场J-Differenct Numbers

【题意】给定 $n$ 个数， $m$ 个查询，每次查询 $I, j$ 要求 $[1, i]$ 和 $[j, n]$ 这2个区间内有多少不同的数字。
【TAG】区间查询铜牌题
【题解】这题在比赛的时候用莫队是有时可以过的。不过赛后似乎加强了数据，原本比赛时候AC的代码赛后重交也TLE了。这里就放一个莫队的做法，不过现在提交是会TLE的。^【20】
【代码_莫队算法版本】nowcoder\2018multi\1J
题库
SPOJ-DQUERY-D-query
CF-86D- Powerful array
Codechef-GERALD07- Chef and Graph Queries
Codechef-GERALD3-Chef and Substrings
CF-375D- Tree and Queries
CF-351D- Jeff and Removing Periods
Codechef- IITI15- Sherlock and Inversions

ST表（Sparse Table）

解决静态RMQ问题（Range Minimum/Maximum Query）区间最值问题^【21】
ST表使用了动态规划的思想。
$d p [i] [j]$ 表示从i开始，长度为 $2^j$ 的区间
比方说对于最小值查询
$d p [i] [j] = m i n (d p [i] [j - 1], d p [i + 1 < < (j - 1)] [j - 1])$
更新的时候就是从区间长度为1的往上更新
查询的时候，比方说给定区间 $（ 5, 10 ）$ 长度为6
那么比这个区间小的最大2的幂次长度的区间为 $2^2$ （这个直接用）
那么拆成2个重叠区间的最小值， $(5, 8)$ 和 $(7, 10)$ ，这2个值都是 $d p$ 中现成的
即 $m i n (5, 10) = m i n (m i n (5, 8), m i n (7, 10))$

ST表与线段树

线段树的时空复杂度：
预处理 $O(nlog_2n)$ ，单次查询 $O(nlog_2n)$ ，空间复杂度 $O (n)$
ST表的时空复杂度：
预处理 $O(nlog_2n)$ ，单次查询 $O (1)$ ，空间复杂度 $O(nlog_2n)$
ST表相比线段树查询更快，空间复杂度更高（空间换时间）
题库
CDOJ-1591-An Easy Problem A-板子题

主席树（可持久化线段树）

可持久化线段树总结（可持久化线段树，线段树）

题库

金牌题-前置：无
2018杭电暑期多校3J-HDU6328-Rectangle Radar Scanner
【题意】
【TAG】区间维护区间查询
【题解】
【代码】
金牌题-前置：无
牛客网2018暑期多校4E-Skyline
【题意】
【TAG】概率线段树
【题解】
TLE-POJ-2155-Matrix
【TAG】二维线段树
【题意】
【题解】【17】

七、数学

指数循环节问题/扩展欧拉定理

牛客网2018暑期多校第4场-A

【题意】一个包含0、1、2的字符串，每秒每个1后面会多1个0，每个2后面会多1个1，在每一秒结束时，第1个字符会被删除。给定字符串（长度 $1 e 5$ ，所有测试数据总长度数量级 $1 e 6$ ），输出该字符串多久变为空串，如果永远不会变为空串，输出-1.
【题解】
解决本题要经过3道关卡
第一关：找规律得到递推式
首先，分析出一个字符串不会永远为空串。考虑1个字符串在第1个2之前出现的第1个1，其之前只有0，所以这个1会在有限时间内被消灭，考虑第1个2之前出现的第2个1，由于它前面的1会在有限的时间被消灭，之后第2个1也会变为与第1个1相同的情形，依次类推，第1个2之前的所有1都会在有限时间内被消灭，因此经过有限时间第1个2之前只有0，因此第1个2也会在有限时间被消灭，此时之后的1和2就相继在有限时间内变成了第1个1和第1个2，同理，所有的数都将在有限时间内被消灭。
考虑当消灭初始串的1个0时，需要花1个单位时间。
而当消灭初始串的1个1时，假定之前已经过去了 $n$ 个单位时间，那么这个1已经繁衍出了 $n$ 个0，于是要花费 $n + 1$ 单位时间才能将初始串的这个1及其后代都消灭。
当消灭初始串的1个2时，假定之前已经过去了 $n$ 个单位时间，则2在这 $n$ 个单位时间的繁衍规律如下：
2
21
2110
2101001000
2110100100010000
输入模拟程序，得到存活序列为
8,19,42，89,184…
（0）找（E）规（I）律（S）后可以发现满足如下式子
$a[n]=3*2^{n+1}-(n+1)-2$
即扫描原串，记录当前已经经过的时间 $t$
遇到 $0$ ， $t = t + 1$
遇到 $1$ ， $t = 2 * t + 2$
遇到 $2$ ， $t=3*2^{t+1}-3$
第二关：正确取模-应用扩展欧拉定理（指数循环节问题）
当通过第1关后就可以过样例了，然后就可喜的WA了。然后就会发现这里会有指数循环取模的问题，所以应用扩展欧拉定理进行解决，要维护模 $\phi(N)、\phi(\phi(N))……$ 的值。
第三关：优化时间复杂度
当弥补了取模的BUG后，就会可喜的发现有TLE了，于是要进行时间复杂度的优化……这里并没有理解的很到位，首先预处理掉要用到的 $\phi$ 值是很好理解的，毕竟这里 $\phi$ 值不多，能节省一些时间复杂度，单单这样还是不能解决TLE的问题。发现了网上可以AC的程序中有一个使用了DFS，可能由于对于上一层phi的维护值不需要算完，于是就可以剪枝。至于标程中顺推过程遇到2的优化，还没有很理解。可以考虑先解决以下问题：指数循环节^【22】
【代码1_dfs版本】nowcoder\2018multi\4A\Solution_dfs.cpp
【代码2_标程-顺推版本（优化方法不明）】nowcoder\2018multi\4A\Solution_standard.cpp

打表

OEIS

OEIS网站^【23】

ICPC2018南京站网络预选赛A题（计蒜客）- An Olympian Math Problem

【TAG】签到题找规律数学阶乘
【题解】尝试打表找规律
【打表】

猜想答案就是 $n - 1$
【打表代码】jisuanke\2018ICPC\nanjing_pre\Enumerate.cpp
【代码】jisuanke\2018ICPC\nanjing_pre\An Olympian Math Problem

快速幂

$2^x$ 次方直接写成1<

一般快速幂

ll fast_pow(ll a,ll b,ll N){
    a%=N;
    ll base=a,ans=1;
    while(b){
        if(b&1) ans=(ans*base)%N;
        b>>=1;
        base=(base*base)%N;
    }
    return ans;
}

根据递推式构造系数矩阵

参考^【24】

矩阵快速幂

快速傅里叶变换（FTT）

快速数论变换（NTT）

快速沃尔什变换（FWT）

参考^【25】

集合

交

并

差

不定积分

HDU-6362-Oval and Rectangle

【source】2018杭电暑期多校第6场1001
【难度】签到题
【TAG】不定积分数学期望概率论
【题解】
求出公式 $\pi a+2b$ 即可
注意推导公式过程中要乘概率密度函数
注意精度（去尾）
【代码】hdu\6362\Solution.cpp

数论

逆元

x对mod求逆元，应用费马小定理 $x^{mod-1}\equiv 1\mod{mod}$ ，x和 $m o d$ 互素，一般题目给的 $m o d$ 本身就是素数，于是 $x^{mod-2}x=x^{mod-1}\equiv 1\mod{mod}$ 所以 $x$ 的逆元就是 $x^{mod-2}$
使用快速幂求解

ll inv(ll x,ll mod)
{
    ll k=mod-2,ans=1;
    while(k)
    {
        if (k&1) ans=(ans*x)%mod;
        x=(x*x)%mod;
        k>>=1;
    }
    return ans;
}

阶乘逆元

fac[0]=fac[1]=1;
for(int i=2;i<=MAXN;i++)fac[i]=fac[i-1]*i%mod;
inv[MAXN]=quipow(fac[MAXN],mod-2);
for(int i=MAXN-1;i>=0;i--)inv[i]=inv[i+1]*(i+1)%mod;

【代码示例】

const long long mod=1000000007;
const int maxn=100000;
typedef long long LL;

LL fac[maxn+9],inv_fac[maxn];

LL quickpow(LL x,LL n)
{
    LL res=1;
    x=x%mod;
    while(n)
    {
        if(n%2==1)res=(res*x)%mod;
        n=n/2;
        x=(x*x)%mod;
    }
    return res;
}


void print()
{
    fac[0]=1;
    for(int i=1;i<=maxn;i++)
        fac[i]=(fac[i-1]*i)%mod;//阶乘取余打表

    //切记,求阶乘逆元时maxn最大值为mod-1，因为用这个公式时要保证待求逆元的数（此处为n!）要和mod互质。

    inv_fac[maxn]=quickpow(fac[maxn],mod-2);//最大阶乘逆元

    for(int i=maxn-1;i>=0;i--)
        inv_fac[i]=(inv_fac[i+1]*(i+1))%mod;//递推阶乘逆元
}

欧拉函数

//单个欧拉值
ll euler(ll x)
{
    ll num=x;
    for (ll i=2ll;i*i<=x;i++)
    {
        if (x%i==0ll)
        {
            num=(num/i)*(i-1ll);
            while (x%i==0ll) x/=i;
        }
    }
    if (x!=1ll) num=(num/x)*(x-1ll);
    return num;
}
//单个欧拉值
//模板未验证
#include 
int GetPhi(int n)
{
    int m = sqrt(n+0.5);
    int ans = n;
    for(int i=2; i<=m; ++i) if(n%i == 0)
    {
        ans = ans/i * (i-1);
        while(n%i == 0) n /= i;
    }
    if(n > 1) ans = ans/n * (n-1);
    return ans;
}
//下面的代码求出了1~n中所有数的欧拉函数值，并保存在了phi数组中
//模板未验证
const int MAXN = 3e6+5;
__int64 phi[MAXN];
 
void PhiTable(int n)
{
    for(int i=2; i<=n; ++i)
        phi[i] = 0;
    phi[1] = 1;
    for(int i=2; i<=n; ++i) if((!phi[i]))
        for(int j=i; j<=n; j+=i)
        {
            if(!phi[j]) phi[j] = j;
            phi[j] = phi[j]/i * (i-1);
        }
}
//求出了1~n中所有数的欧拉函数值的前缀和，并保存在了f数组中
//模板未验证
const int MAXN = 3e6+5;
__int64 f[MAXN];
void SumPhiTable(int n)
{
    f[1] = 1;
    for(int i=2; i<n; ++i)
    {
        if(!f[i])
        {
            for(int j=i; j<n; j+=i)
            {
                if(!f[j]) f[j] = j;
                f[j] = f[j]/i * (i-1);
            }
        }
        f[i] += f[i-1];
    }
}

威尔逊定理

p为素数，则((p-1)! + 1) % p == 0

幂取模(欧拉定理、费马小定理、扩展欧拉定理)

欧拉定理

$a, p$ 互质
$a^{\varphi(p)}\equiv 1\mod{p}$
$a^b\%p=a^{b\%\varphi(p)}\%p$

费马小定理

$a, p$ 互质且 $p$ 为质数则 $\varphi(p)=p-1$
$a^{p-1}\equiv 1\mod{p}$
$a^b\%p=a^{b\%(p-1)}\%p$

扩展欧拉定理

（不要求a,c互质）

当x

指数循环节问题

https://blog.csdn.net/acdreamers/article/details/8236942
FZU-1759
HDU-2837
ZOJ-1674
HDU-4335
https://blog.csdn.net/wust_zzwh/article/details/51966450
（HDU-5728-2016多校）

不定方程

√-HDU-6298-2018多校1-签到题

【题意】

【题解]

【代码】hdu\6298

综合题

√-ECNU ICPC/CCPC Trial Round #1-M-Memory Penalty

【TAG】签到题
【题意】求1,2,3,…,n中某一段区间，使得和为给定数字，并且区间长度最大

【代码】eoj\ICPC CCPC Trial Round#1-M-Memory Penalty

组合数学

组合数

https://blog.csdn.net/u010582475/article/details/47707739
求1个组合数，使用递推公式O(n)求解
求n个组合数，可以预处理阶乘逆元，O(n)求解，参考阶乘逆元

卢卡斯定理

LL Lucas(LL a, LL b)
{
    if(a < mod && b < mod)
        return C(a, b);
    return
        C(a % mod, b % mod) * Lucas(a / mod, b / mod);
}

https://blog.csdn.net/liangzhaoyang1/article/details/52132986?locationNum=7

卡特兰数

出栈次序
二叉树构成
凸多边形的三角形划分

Polya定理

https://www.bilibili.com/video/av6357073?from=search&seid=4827637457650479048

原理不会-HDU-3923-Invoker

【题意】n种元素（可以同一种元素拿多个）放m个位置，经过旋转和翻转重合的算一种，统计总的个数
【题解】应用（Burnsid引理）Polya定理，目前还不会
【参考AC代码】hdu\3923

HDU-1812-Count Teris

【题意】n*n的棋盘，用c种颜色染色，（旋转、反射算一种），问有多少种不同棋盘。
数据规模 n,c<31
【题解】
【代码】

计算几何

http://dev.gameres.com/Program/Abstract/Geometry.htm#

点到线段的最短距离——矢量法

const double eps=1e-6;
int fcmp(double x){
    if (fabs(x)<=eps) return 0;
    return x<0?-1:1;
}

double PointToSegDist(double px, double py, double xa, double ya, double xb, double yb){
    double AP_AB=(px-xa)*(xb-xa)+(py-ya)*(yb-ya);
    double AB_AB=(xb-xa)*(xb-xa)+(yb-ya)*(yb-ya);
    double AB=sqrt(AB_AB);
    double k=AP_AB/AB_AB;
    double AP_AP=(px-xa)*(px-xa)+(py-ya)*(py-ya);
    double AP=sqrt(AP_AP);
    double BP_BP=(px-xb)*(px-xb)+(py-yb)*(py-yb);
    double BP=sqrt(BP_BP);
    if (fcmp(k)<0){
        return AP;
    }else if (fcmp(k-1)<=0){
        double d=sqrt(AP_AP-(AP_AB/AB)*(AP_AB/AB));
        return d;
    }else{
        return BP;
    }
}

√-51nod-1298-圆与三角形

【题干】
给出圆的圆心和半径，以及三角形的三个顶点，问圆同三角形是否相交。相交输出"Yes"，否则输出"No"。（三角形的面积大于0）。
【题解】
圆与三角形是否相交转换为圆与三角形的每一条边是否相交，圆与一条线段相交的条件是圆心到线段的距离小于等于半径且线段的端点至少有一个在圆外（含边）
【代码】51nod\1298

四点共面

√-51nod-1265-四点共面

【题意】输入4个点判断是否在同一平面
【题解】使用如下公式进行判断

【代码】51nod\1265

线段相交

√（模板）-51nod-1264

【题意】输入2个线段的4个端点，判断是否相交
【题解】直接使用浙大计算几何模板（1.5浮点数），注意该模板使用时不能加using namespace std;

简单多边形与圆面积交

√-牛客网2018暑期多校第3场-J（简单多边形与圆面积交）

【题意】给定简单多边形（定点顺时针或逆时针给出），给定圆心，要求圆的和简单多边形的面积交为给定值，输出圆的半径,坐标绝对值1000以内,n最多300
【题解】使用模板简单多边形与圆面积交和凸多边形面积，这里二分半径r即可（最小0，最大3000）
【代码】nowcoder\2018multi\3J

两圆相交点

https://blog.csdn.net/u013021513/article/details/43984497

两圆相交弧长

√-HDU-6354-Everything Has Changed

【source】2018杭电暑期多校第5场1005-签到题
【题意】如图给定一个大圆，再给定若干其他圆，求图中红色部分的长度和，给定的若干其他圆不会相交。

【TAG】计算几何签到题弧长圆圆相交优弧劣弧
【题解】

可见优劣弧的情况下D的表达式都是一样的，所以只需要处理圆心角的不同即可
有可能给定的圆会大于原本的圆，这时候需要分类讨论，只要把上述情况中的R和r进行交换即可。
比赛的时候从头WA到尾，赛后对拍应该是哪里写错了而不是精度问题，有地方double炸了，可能开根号开出负的了。
【代码】hdu\6354

极角排序

凸包

其他题目

√-HDU-5858-2016多校10-签到

【题意】求阴影部分面积
【公式】

线性规划

单纯形法

http://www.cnblogs.com/zzqsblog/p/5457091.html
https://blog.csdn.net/u010336344/article/details/62422284
https://www.bilibili.com/video/av7847726?from=search&seid=8839682959904581481
http://www.doc88.com/p-846811841036.html
https://blog.csdn.net/hdu2014/article/details/51124340
https://blog.csdn.net/u012116229/article/details/44205943
https://blog.csdn.net/alan_cty/article/details/71716617

2018百度之星资格赛1003-应该就是单纯形法

【题目】

【模板代码】//偏工程的代码，目前没有拿他调通过题目,可以作为对拍
baidustar\2018zigesai\1003

综合题

√-牛客网2018暑期多校第1场-A（OEIS打表&组合数递推&逆元）

【题意】一个nm的矩阵，只包含0,1,2这3种数字，要求从左至右递增，从上至下递增，求符合条件的矩阵个数，数据规模，测试数据组数最多
【题解】
允许使用OEIS是铜牌题，不允许则是金牌题
合理的可以做的解题思路：
首先打表，接着在OEIS上查询
短时间大约能打88左右

拿着结果一行一行的到OEIS上查询
第1行到第6行每一行都能查询出一个不同的公式，但并没有明显的通用规律
第7行开始输进去，神奇的事情发生了

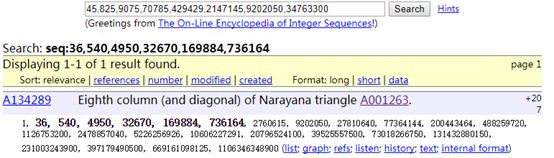
它说这是一个什么三角形的第8行，点开这个A001263

看到了一个通用公式，且其别名为Catalan三角形
以table形式显示

这显然就是我们打表出来的答案，所以初步肯定上面的通式就是本题的答案


并不是直接与我们上面那个表一一对应的，找到这里面出现的数字在我们上一张表中出现的位置的规律，发现这里面的每一行都是我们打表答案中的每一个斜行（对角行），再调整一下行列偏移，得到公式 $f (n, m) = T (n + m + 1, m + 1)$
这里面由于数字较大要对N取模，考虑到T的公式中出现除法，故还要使用逆元将/k变为*(inv(k))，同时开long long，注意分步取模
这里逆元用的板子的思路是根据费马小定理，a对p的逆元就是a^(p-2)，使用快速幂求解
标准官方解题思路（看看就好）：
考虑 01 和 12 的分界线
是 (n, 0) 到 (0, m) 的两条不相交（可重合）路径
平移其中一条变成 (n-1, -1) 到 (-1, m-1)
变成起点 (n, 0) 和 (n-1, -1)，终点 (0, m) 和 (-1, m-1) 的严格不相交路径
套 Lindström–Gessel–Viennot lemma
答案是 Cn+m, n 2 - Cn+m, m - 1 Cn+m, n-1
【代码】nowcoder\2018multi\1A

√-HDU-6304-2018多校1-铜牌题

【题意】

n范围10^{18，测试数据10}5

【代码】hdu\6304

√-EOJ-110-2018月赛7-数蝌蚪-签到题

【题意】n个数，要求变为公差为k的等差数列（均要为正），对每个数可以加1或减1算1次操作，求最小操作数
【题解】
【代码】eoj\110

√-HDU-6333-Harvest of Apples

【source】2018杭电暑期多校4B

用上述关系直接应用莫队算法即可。
【代码】hdu\6333

题库

银牌题-前置：凸包/随机化算法
牛客网2018暑期多校3I-Expected Size of Random Convex Hull
【题意】
【TAG】凸包
【题解】
【代码】
铜牌题-前置：凸包
2018杭电暑期多校3G-HDU6325-Instellar Travel
【题意】
【TAG】计算几何凸壳
【题解】
【代码】
（队友AC）签到题-前置：无
2018杭电暑期多校3F-Grab The Tree-HDU6324
【题意】
【TAG】异或二进制博弈
【题解】
【代码】
（队友AC）签到题-前置：无
2018杭电暑期多校3D-HDU6322-Euler Function
【题意】
【TAG】数论欧拉函数
【题解】
【代码】
（队友AC）签到题-前置：无
2018杭电暑期多校4L-HDU6343-Graph Theory Homework
【题意】
【TAG】数学最短路签到题
【题解】
【代码】
（队友AC）签到题-前置：无
2018杭电暑期多校2J-HDU6318-Swaps and Inversions
【题意】
【TAG】逆序对签到题
【题解】
【代码】
（队友AC）签到题-前置：无
2018杭电暑期多校1A-HDU6298-Maximum Multiple
【题意】
【TAG】数论签到题
【题解】
【代码】
（队友AC）签到题-前置：无
牛客网2018暑期多校3H-Diff-Prime Pairs
【题意】
【TAG】数论签到题
【题解】
【代码】
银牌题-前置：无
2018杭电暑期多校2F-HDU6314-Matrix
【题意】
【TAG】容斥组合数
【题解】
【代码】
金牌题-前置：莫比乌斯反演/伯努利数/卷积/NTT
2018杭电暑期多校4I-HDU6340-Delightful Formulas
【题意】
【TAG】
【题解】
【代码】
金牌题-前置：多项式插值
2018杭电暑期多校2B-HDU6310-Counting Permutations
【题意】
【TAG】数学多项式插值
【题解】
【代码】
金牌题-前置：Freshman’s Dream
2018杭电暑期多校2H-HDU6316-Odd Shops
【题意】
【TAG】
【题解】
【代码】
金牌题-前置：矩阵秩
牛客网2018暑期多校1C-Fluorescent 2
【TAG】数学矩阵秩
银牌题-前置：拉格朗日插值
牛客网2018暑期多校1F-Sum of Maximum
【TAG】数学拉格朗日插值

八、网络流

最大流

最小费用最大流

模板

//求网络最小费用最大流,邻接阵形式
//返回最大流量,flow返回每条边的流量,netcost返回总费用
//传入网络节点数n,容量mat,单位费用cost,源点source,汇点sink
#include
#define MAXN 210
#define inf 1000000000
using namespace std;
int min_cost_max_flow(int n,int mat[][MAXN],int cost[][MAXN],int source,int sink,int flow[][MAXN],int& netcost){
       int pre[MAXN],min[MAXN],d[MAXN],i,j,t,tag;
       if (source==sink) return inf;
       for (i=0;i<n;i++) for (j=0;j<n;flow[i][j++]=0);
       for (netcost=0;;){
              for (i=0;i<n;i++) pre[i]=0,min[i]=inf;
              for (pre[source]=source+1,min[source]=0,d[source]=inf,tag=1;tag;)
                     for (tag=t=0;t<n;t++)
                            if (d[t])
                                   for (i=0;i<n;i++)
                                          if (j=mat[t][i]-flow[t][i]&&min[t]+cost[t][i]<min[i])
                                 tag=1,min[i]=min[t]+cost[t][i],pre[i]=t+1,d[i]=d[t]<j?d[t]:j;
                                          else if (j=flow[i][t]&&min[t]<inf&&min[t]-cost[i][t]<min[i])
                                                 tag=1,min[i]=min[t]-cost[i][t],pre[i]=-t-1,d[i]=d[t]<j?d[t]:j;
              if (!pre[sink])  break;
              for (netcost+=min[sink]*d[i=sink];i!=source;)
                     if (pre[i]>0)
                            flow[pre[i]-1][i]+=d[sink],i=pre[i]-1;
                     else
                            flow[i][-pre[i]-1]-=d[sink],i=-pre[i]-1;
       }
       for (j=i=0;i<n;j+=flow[source][i++]);
       return j;
}

√-牛客网2018暑期多校5E-room

【题意】给定n个旧寝室组合和n个新寝室组合，问从旧寝室组合调整到
【TAG】最小费用最大流网络流建图铜牌题
【题解】每个旧寝室组合和新寝室组合都看成1个点，每个旧寝室组合和新寝室组合之间都有一条边，容量为1，最后最大流就是满流的情况，如果有流量流过这条边，就代表这个新寝室组合将会住进这个旧寝室组合所住的那个寝室，费用就是（4-新旧寝室相同人数），即这个新寝室组合住到这个旧寝室组合所在寝室会导致这个新寝室组合中有多少人换寝室。加上源点和汇点即可。
注意模板中的MAXN的值要做调整，否则可能段溢出。
【代码-使用最小费用最大流模板】nowcoder\2018multi\5E

二分图匹配

定理
无向图G=为二分图的充要条件是G的所有回路的长度均为偶数。
最大匹配
在G的一个子图M中，M的边集中的任意两条边都不依附于同一个顶点，则称M是一个匹配。选择这样的边数最大的子集称为图的最大匹配问题,最大匹配的边数称为最大匹配数.如果一个匹配中，图中的每个顶点都和图中某条边相关联，则称此匹配为完全匹配，也称作完备匹配。如果在左右两边加上源汇点后，图G等价于一个网络流，最大匹配问题可以转为最大流的问题。解决此问的匈牙利算法的本质就是寻找最大流的增广路径。
最优匹配
最优匹配又称为带权最大匹配，是指在带有权值边的二分图中，求一个匹配使得匹配边上的权值和最大。一般X和Y集合顶点个数相同，最优匹配也是一个完备匹配，即每个顶点都被匹配。如果个数不相等，可以通过补点加0边实现转化。一般使用KM算法解决该问题。
最小覆盖
二分图的最小覆盖分为最小顶点覆盖和最小路径覆盖：
最小顶点覆盖是指最少的顶点数使得二分图G中的每条边都至少与其中一个点相关联，二分图的最小顶点覆盖数=二分图的最大匹配数；
最小路径覆盖也称为最小边覆盖，是指用尽量少的不相交简单路径覆盖二分图中的所有顶点。二分图的最小路径覆盖数=|V|-二分图的最大匹配数；
最大独立集
最大独立集是指寻找一个点集，使得其中任意两点在图中无对应边。对于一般图来说，最大独立集是一个NP完全问题，对于二分图来说最大独立集=|V|-二分图的最大匹配数。
匈牙利算法
初始时最大匹配为空
while 找得到增广路径 do 把增广路径加入到最大匹配中去
增广路径
(1)有奇数条边。
(2)起点在二分图的左半边，终点在右半边。
(3)路径上的点一定是一个在左半边，一个在右半边，交替出现。
(4)整条路径上没有重复的点。
(5)起点和终点都是目前还没有配对的点，而其它所有点都是已经配好对的。
(6)路径上的所有第奇数条边都不在原匹配中，所有第偶数条边都出现在原匹配中。
(7)把增广路径上的所有第奇数条边加入到原匹配中去，并把增广路径中的所有第偶数条边从原匹配中删除（这个操作称为增广路径的取反），则新的匹配数就比原匹配数增加了1个。定理
如果从一个点A出发，没有找到增广路径，那么无论再从别的点出发找到多少增广路径来改变现在的匹配，从A出发都永远找不到增广路径。
应用定理描述匈牙利算法
初始时最大匹配为空
for 二分图左半边的每个点i
do 从点i出发寻找增广路径。如果找到，则把它取反（即增加了总了匹配数）

√-51nod-2006-飞行员配对

Input
第1行有2个正整数 m 和 n。n 是皇家空军的飞行员总数(n<100);m 是外籍飞行员数。外籍飞行员编号为 1~m;英国飞行员编号为 m+1~n。接下来每行有 2 个正整数 i 和 j，表示外籍飞行员 i 可以和英国飞行员 j 配合。输入最后以 2 个-1 结束。
Output
第 1 行是最佳飞行员配对方案一次能派出的最多的飞机数 M。如果所求的最佳飞行员配对方案不存在，则输出‘No Solution!’。
Input示例

5 10
1 7
1 8
2 6
2 9
2 10
3 7
3 8
4 7
4 8
5 10
-1 -1

Output示例

4

【代码】51nod\2006

上下界网络流

模板

const int inf=1000000000;
const int maxn=20000,maxm=500000;
struct dinic{
    struct Edge{
        int v,f,nxt;
    };
    int n,src,sink;
    int g[maxn+10];
    int nume;
    Edge e[maxm*2+10];
    void addege(int u,int v,int c){
        e[++nume].v=v;
        e[nume].f=c;
        e[nume].nxt=g[u];
        g[u]=nume;
        e[++nume].v=u;
        e[nume].f=0;
        e[nume].nxt=g[v];
        g[v]=nume;
    }
    void init(){
        memset(g,0,sizeof(g));
        nume=1;
    }
    queue<int> que;
    bool vis[maxn+10];
    int dist[maxn+10];
    void bfs(){
        memset(dist,0,sizeof(dist));
        while(!que.empty()) que.pop();
        vis[src]=true;
        que.push(src);
        while(!que.empty()){
            int u=que.front();
            que.pop();
            for(int i=g[u];i;i=e[i].nxt)
            if(e[i].f&&!vis[e[i].v]){
                que.push(e[i].v);
                dist[e[i].v]=dist[u]+1;
                vis[e[i].v]=true;
            }
        }
    }
    int dfs(int u,int delta){
        if(u==sink){
            return delta;
        }else{
            int ret=0;
            for(int i=g[u];delta&&i;i=e[i].nxt)
            if(e[i].f&&dist[e[i].v]==dist[u]+1){
                int dd=dfs(e[i].v,min(e[i].f,delta));
                e[i].f-=dd;
                e[i^1].f+=dd;
                delta-=dd;
                ret+=dd;
            }
            return ret;
        }
    }
    int maxflow(){
        int ret=0;
        while(true){
            memset(vis,0,sizeof(vis));
            bfs();
            if(!vis[sink]) return ret;
            ret+=dfs(src,inf);
        }
    }

}DINIC;

bool lowbound_flow(int n,int source,int sink,vector<int> u,vector<int> v,vector<int> L,vector<int> U){
        DINIC.init();
        vector<int> tot_in(n+1),tot_out(n+1);
        for(int i=0;i<(int)u.size();++i){
            if(U[i]<L[i]){
                return 0;
            }
            tot_in[v[i]]+=L[i];
            tot_out[u[i]]+=L[i];
            DINIC.addege(u[i],v[i],U[i]-L[i]);
        }
        DINIC.addege(sink,source,1000000000);
        int super_source=n+1;
        int super_sink=n+2;
        DINIC.src=super_source;
        DINIC.sink=super_sink;
        for(int i=1;i<=n;++i){
            DINIC.addege(super_source,i,tot_in[i]);
            DINIC.addege(i,super_sink,tot_out[i]);
        }
        int ans=DINIC.maxflow();
        //cout<
        for(int i=DINIC.g[super_source];i;i=DINIC.e[i].nxt){
            if(DINIC.e[i].f!=0){
                return 0;
            }
        }
        return 1;
}

√-ICPC网络预选赛沈阳站-F- Fantastic Graph

【Source】计蒜客
【TAG】上下界网络流网络流
【题解】比较裸的上下界网络流，注意我用的板子的建图里面下标要从1开始
【代码】jisuanke\2018ICPC\shenyang_pre\F

题库

银牌题-KM匹配
2018百度之星程序设计大赛资格赛-1002
【题意】
【TAG】整数规划 KM匹配
【代码】
【网上AC代码】

#include
using namespace std;
typedef long long ll;
const int inf=0x7f7f7f7f;
const int N=1010,M=1000100;

int TT,n,labx[N],laby[N],xx[N],yy[N],pre[N];
int e[N][N],q[N],flag[M],slack[N];
ll ans;

void find(int x){    
    for(int p;x;p=xx[pre[x]],yy[x]=pre[x],xx[pre[x]]=x,x=p);
}
void KM(int S){
    memset(flag,0,sizeof(flag));
    memset(slack,63,sizeof(slack));
    flag[q[1]=S]=1;
    for(int l=1,r=2;;){
        while(l<r){
            int x=q[l++]; 
            for(int y=1;y<=n;y++){
                int tmp=labx[x]+laby[y]-e[x][y];
                if(flag[yy[y]]||slack[y]<tmp) continue;
                pre[y]=x;
                if(!tmp){
                    if(!yy[y]) return find(y);
                    q[r]=yy[y]; flag[q[r]]=1;r++;
                }else slack[y]=tmp;
            }
        }
        int delta=inf; 
        for(int i=1;i<=n;i++)
            if(!flag[yy[i]]) delta=min(delta,slack[i]);
        for(int i=1;i<=n;i++){
            if(flag[i]) labx[i]-=delta;
            if(flag[yy[i]]) laby[i]+=delta;
            else slack[i]-=delta;
        }
        for(int i=1;i<=n;i++) if(!flag[yy[i]]&&!slack[i]){
            if(!yy[i]) return find(i);
            q[r]=yy[i]; flag[q[r]]=1;r++;
        }
    }
}
void KM(){
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
        labx[i]=max(labx[i],e[i][j]);
    for(int i=1;i<=n;i++)KM(i);
}

int main(){
    scanf("%d",&TT);
    for(int T=1;T<=TT;T++){ 
        scanf("%d",&n); ans=0;
        for(int i=1;i<=n;i++) for(int j=1;j<=n;j++)
            scanf("%d",&e[i][j]),e[i][j]*=-1;
        KM();
        for(int i=1;i<=n;i++) ans+=labx[i]+laby[i];
        printf("Case #%d: %I64d\n",T,-ans);
        memset(labx,0,sizeof(labx));
        memset(laby,0,sizeof(laby));
        memset(xx,0,sizeof(xx));
        memset(yy,0,sizeof(yy));
        memset(pre,0,sizeof(pre));
    }
    return 0;
}

未做-hdu-2063

九、博弈

√-51nod-1995-三子棋

【题干】
Input
第一行输入一个整数T，表示数据组数（1 第二行输入两个整数x,y,表示3×4格子里面的一个坐标(x,y)（1<=x<=3,1<=y<=4）；
Output
每组数据输出最后小明输赢的结果，如果小明一定能赢，第一行输出“Win”,第二行输出小明所需要花的最少步数；如果小明跟小花只能打成平手，第一行输出“Equal”，第二行输出数字0；如果小明不能赢也不能跟小花打成平手，第一行输出“Lose”,第二行输出小花赢小明所需要花的最少步数。
Input示例

2
2 1
2 4

Output示例

Equal
0
Equal
0

【思路】
将3*4的棋盘分成4种类型的位置（对称）
第1种（1,1）（1,4）（3,1）（3,4）枚举后手的第1个位置，都有必赢策略，其中最多需要6步
第2种（1,2）（1,3）（3,2）（3,3）枚举后手的第1个位置，都有必赢策略，其中最多需要4步
第3种（2,2）（2，3）枚举后手的第1个位置，都有必赢策略，其中最多需要4步
第4种（2,1）（2，4）根据题目样例，平局
【AC代码】51nod\1995

√-HDU-6312-多校2-签到题

【题意】1-n这n个正数，每个人可以拿走1个数连带它的所有因子都被拿走，谁先拿完谁赢，Alice先手，给定n问Alice是否有必赢策略。数据规模n为500
【题解】
比赛的时候先手算打表，一直算到n=7都是Alice赢，这时才开始比赛没几分钟，这题过的人已经井喷了，于是队友说估计是全Yes了，又稍微想了一会儿，交了果然全Yes…
具体严格的原因还没有想清楚。当时考虑到的一个就是如果剩下的都是互相互素的数的话，那么轮到一个人又偶数个的局就必输，反之奇数个就必赢。
赛后群里发的题解是“考虑将游戏变成初始时只有2~n，如果先手必胜的话，那么先手第一步按这样取就获胜了；如果后手必胜的话，那么先手第一步取走1就获胜了。所以全输出Yes就行了。”这有点强。。不过这个里面似乎没有出现题目中所要求的什么拿走因子之类的。。所以这个套路看来对很多种博弈都有效？（开局1-n，先手可以拿走1，谁先拿光谁赢，其他的拿法可以是任意某种确定的拿法）哦，不对，这里因为2-n里面随便拿走某一个都会导致1的被拿走，这一点是由本题的性质所决定的。

十、随机算法

随机除了可应用与某些随机算法的题目，还可以在代码提交前对代码进行大量的随机测试以判定代码是否正确

函数库

//随机序列
#include 
int a[100];
random_shuffle(a,a+n);
vector<int> a;
random_shuffle(a.begin(),a.end());

//生成一定范围内随机数
#include 
#include 
srand((unsigned)time(NULL));//用这个提交OJ可能会错，换成srand(i)尝试；
产生一定范围随机数的通用表示公式是：
取得(0,x)的随机整数：rand()%x；
取得(a,b)的随机整数：rand()%(b-a)；
取得[a,b)的随机整数：rand()%(b-a)+a；
取得[a,b]的随机整数：rand()%(b-a+1)+a；
取得(a,b]的随机整数：rand()%(b-a)+a+1；
取得0-1之间的浮点数：rand()/double(RAND_MAX)。

十一、其他

莫队算法
https://blog.csdn.net/hnshhslsh/article/details/50582926
https://www.cnblogs.com/137shoebills/p/7783739.html
https://blog.csdn.net/thinfatty/article/details/72581276
√-HDU-5857-2016多校10-签到
√-HDU-5867-2016多校10-签到

第三部分专项题库

https://blog.csdn.net/liuqiyao_01/article/details/9079611
ACM题集以及各种总结大全
https://blog.csdn.net/lingzidong/article/details/78472208
2013-2017 ACM/ICPC 区域赛&final 水题和铜牌题
https://blog.csdn.net/acm_1361677193/article/details/42873141
叉姐的训练指南
https://blog.csdn.net/qq_40688707/article/details/80602064
ACM训练史上最详细计划（大神养成记）
http://www.cnblogs.com/autsky-jadek/

杭电多校题库（2011-2017）

签到题&铜牌题库

6092
6095
6069
6070
6075
6077
6058
6060
6063
6066
6045
6047
6050
6053
6055
6033
6034
6035
6038
6043
5855
5821
5826
5828
5831
5810
5813
5816
5818
5793
5794
5795
5781
5783
5787
5791
5792
5763
5768
5769
5773
5774
5775
5752-5754
5761-5762
5734
5738
5742
5744
5745
5723
5724
5726
5733
5407
5410
5411
5412
5414
5416
5396
5399
5400
5402
5384
5386-5387
5389
5371
5373
5375
5379
5353
5355
5358
5360
5363
5344
5347
5348
5349
5351
5327
5328
5335
5336
5316
5317
5319
5323
5325-5326
5301
5305
5308
5288
5289
5294

银牌题库

6161
6164
6167
6169
6133
6136
6139
6141
6122
6125
6128
6096-6097
6102
6107
6093
6068
6071
6073
6074
6076
6078
6057
6059
6061
6064
6065
6046
6048-6049
6052
6040
6044
5845
5852-5853
5823
5829
5811-5812
5814-5815
5819-5820
5800
5802
5782
5784-5785
5765
5772
5755
5758
5735
5739
5741
5727
5729-5731
5406
5409
5413
5398
5401
5381
5385
5372
5374
5378
5357
5361
5362
5352
5334
5338
5318
5303
5299

金牌题库

6173-6177
6179
6163
6135
6137
6142
6120
6123
6126
6131-6132
6099-6101
6104
6087-6089
6091
6094
6067
6072
6079
6056
6062
6051
6054
6036-6037
6039
6041-6042
5844
5846-5851
5854
5856
5822
5824-5825
5827
5830
5809
5817
5796-5799
5801
5803
5786
5788-5790
5764
5766
5770-5771
5756-5757
5759-5760
5736-5737
5740
5743
5746
5725
5728
5732
5408
5415
5397
5403-5405
5380
5382-5383
5388
5390
5369-5370
5376-5377
5354
5356
5359
5343
5345-5346
5350
5329-5333
5337
5320-5322
5324
5300
5302
5304
5306-5307
5309
5290-5293
5295-5298

2018多校
2017多校-已处理
2016多校-已处理
2015多校-已处理
2014多校
10
9
8
7
6
5
4
3
2
1
2013多校
10
9
8
7
6
5
4
3
2
1
2012多校
10
9
8
7
6
5
4
3
2
1
2011多校
10
9
8
7
6
5
4
3
2
1

签到题题库

51nod（一级算法题）

1995-√
2006-√
1459-√
1384-√
1298-√
1265-√
1264-√（计算几何模板）
1205
1256
1240
1242
1212
1185
1183
1181
1079
1174
1137
1136
1135
1134
未完，共44题，上述快要做完时再补充展开，基础级完成后进入1级

补题题库（签到或专项）

ACM作业20180613-数学专题
FZU-1851-ACM作业20180613-签到/铜
HDU-2204-ACM作业20180613-签到/铜
HDU-1796-ACM作业20180613-签到/铜
HDU-1685-ACM作业20180613-签到/铜
UVA-1025-ACM作业20180606-签到/铜
UVA-437-ACM作业20180606-签到/铜
UVA-11584-ACM作业20180606-签到/铜
UVA-1256-ACM作业20180606-签到/铜
UVA-10003-ACM作业20180606-签到/铜
UVA-11400-ACM作业20180606-签到/铜
HDU-1502-ACM作业20180606-签到/铜

单调队列&单调栈

https://wenku.baidu.com/view/5f7222d3b14e852458fb57a2.html
（已完结）
已处理-HDU 3415
已处理-HDU 3530
已处理-POJ 2796

动态规划

背包-进阶
（https://blog.csdn.net/eagle_or_snail/article/details/50987044）
一、简单基础dp
这类dp主要是一些状态比较容易表示，转移方程比较好想，问题比较基本常见的。主要包括递推、背包、LIS（最长递增序列），LCS（最长公共子序列），下面针对这几种类型，推荐一下比较好的学习资料和题目。
1、递推：
递推一般形式比较单一，从前往后，分类枚举就行。
推荐：
zoj 3747 Attack on Titans
uva 10328 Coin Toss
hdu 4747 Mex
hdu 4489 The King’s Ups and Downs
hdu 4054 Number String
hdu 3369 矩阵快速幂（递推式构造系数矩阵）
hdu 3483 矩阵快速幂（递推式构造系数矩阵）
2、背包
经典的背包九讲：http://love-oriented.com/pack/
推荐博客：http://blog.csdn.net/woshi250hua/article/details/7636866
主要有0-1背包、完全背包、分组背包、多重背包。
简单：
hdu 2955 Robberies
hdu 1864 最大报销额
hdu 2602 Bone Collector
hdu 2159 FATE
推荐：
woj 1537 A Stone-I
woj 1538 B Stone-II
poj 1170 Shopping Offers 状压+背包
zoj 3769 Diablo III 带限制条件的背包
zoj 3638 Fruit Ninja 背包的转化成组合数学
hdu 3092 Least common multiple 转化成完全背包问题
poj 1015 Jury Compromise 扩大区间+输出路径
3、LIS
最长递增子序列，朴素的是o(n^2)算法，二分下可以写成o(nlgn)：维护一个当前最优的递增序列——找到恰好大于它更新
推荐：
uva 10635 Prince and Princess LCS转化成LIS
hdu 4352 XHXJ’s LIS　数位dp+LIS思想
srm div2 1000 状态压缩+LIS
poj 1239 Increasing Sequence 两次dp
4、LCS
最长公共子序列，通常o(n^2)的算法
uva 111 History Grading 要先排个序
poj 1080 Human Gene Functions
二、区间dp
推荐博客：http://blog.csdn.net/woshi250hua/article/details/7969225
区间dp,一般是枚举区间，把区间分成左右两部分，然后求出左右区间再合并。
hdu 4745 Two Rabbits 转化成求回文串
zoj 3541 The Last Puzzle 贪心+区间dp
poj 2955 Brackets
hdu 4283 You Are the One 常见写法
hdu 2476 String Printer
zoj 3537 Cake
CF 149D Coloring Brackets
zoj 3469 Food Delivery
三、树形dp
比较好的博客：http://blog.csdn.net/woshi250hua/article/details/7644959
一篇论文：http://doc.baidu.com/view/f3b19d0b79563c1ec5da710e.html
树形dp是建立在树这种数据结构上的dp,一般状态比较好想，通过dfs维护从根到叶子或从叶子到根的状态转移。
hdu 4514 求树的直径
poj 1655 Balancing Act
hdu 4714 Tree2Cycle 思维
hdu 4616 Game
hdu 4126 Genghis Kehan the Conqueror MST+树形dp 比较经典
hdu 4756 Install Air Conditioning MST+树形dp 同上
hdu 3660 Alice and Bob’s Trip 有点像对抗搜索
CF 337D Book of Evil 树直径的思想思维
hdu 2196 Computer 搜两遍
四、数位dp
推荐一篇论文：http://wenku.baidu.com/view/d2414ffe04a1b0717fd5dda8.html
数位dp,主要用来解决统计满足某类特殊关系或有某些特点的区间内的数的个数，它是按位来进行计数统计的，可以保存子状态，速度较快。数位dp做多了后，套路基本上都差不多，关键把要保存的状态给抽象出来，保存下来。
CF 401D Roman and Numbers 状压+数位dp
hdu 4398 X mod f(x) 把模数加进状态里面
hdu 4734 F(x) 简单数位dp
hdu 3693 Math teacher’s homework 思维变换的数位dp
hdu 4352 XHXJ’s LIS　数位dp+LIS思想
CF 55D Beautiful Numbers 比较巧妙的数位dp
hdu 3565 Bi-peak Numbers 比较难想
CF 258B Little Elephant and Elections 数位dp+组合数学+逆元
五、概率(期望) dp
推荐博客：http://www.cnblogs.com/kuangbin/archive/2012/10/02/2710606.html
推荐博客：http://blog.csdn.net/woshi250hua/article/details/7912049
推荐论文：
《走进概率的世界》
《浅析竞赛中一类数学期望问题的解决方法》
《有关概率和期望问题的研究》
一般来说概率正着推，期望逆着推。有环的一般要用到高斯消元解方程。期望可以分解成多个子期望的加权和，权为子期望发生的概率，即 E(aA+bB+…) = aE(A) + bE(B) +…
ural 1776 Anniversiry Firework 比较基础
hdu 4418 Time travel 比较经典BFS+概率dp+高斯消元
hdu 4586 Play the Dice 推公式比较水
hdu 4487 Maximum Random Walk
jobdu 1546 迷宫问题高斯消元+概率dp+BFS预处理
hdu 3853 LOOPS 简单概率dp
hdu 4405 Aeroplane chess 简单概率dp,比较直接
hdu 4089 Activation 比较经典
poj 2096 Collecting Bugs 题目比较难读懂
zoj 3640 Help me Escape 从后往前，比较简单
hdu 4034 Maze 经典好题，借助树的概率dp
hdu 4336 Card Collector 状态压缩+概率dp
六、状态压缩dp
这类问题有TSP、插头dp等。
推荐论文：http://wenku.baidu.com/view/ce445e4f767f5acfa1c7cd51.html
推荐博客：http://blog.csdn.net/sf____/article/details/15026397
推荐博客：http://www.notonlysuccess.com/index.php/plug_dp/
hdu 4568 Hunter 最短路+TSP
hdu 4539 插头dp
hdu 4529 状压dp
poj 1185 炮兵阵地
hdu 3811 Permutation
poj 2411 Mandriann’s Dream
poj 1038
poj 2441
hdu 2167
hdu 4026
hdu 4281
七、数据结构优化的dp
有时尽管状态找好了，转移方程的想好了，但时间复杂度比较大，需要用数据结构进行优化。常见的优化有二进制优化、单调队列优化、斜率优化、四边形不等式优化等。
1、二进制优化
主要是优化背包问题，背包九讲里面有介绍，比较简单，这里只附上几道题目。
hdu 1059 Diving
hdu 1171 Big Event in Hdu
poj 1048 Follow My Magic
2、单调队列优化
推荐论文：http://wenku.baidu.com/view/4d23b4d128ea81c758f578ae.html
推荐博客：http://www.cnblogs.com/neverforget/archive/2011/10/13/ll.html
hdu 3401 Trade
poj 3245 Sequece Partitioning 二分+单调队列优化
3、斜率优化
推荐论文：用单调性优化动态规划
推荐博客：http://www.cnblogs.com/ronaflx/archive/2011/02/05/1949278.html
hdu 3507 Print Article
poj 1260 Pearls
hdu 2829 Lawrence
hdu 2993 Max Average Problem
4、四边形不等式优化
推荐博客：http://www.cnblogs.com/ronaflx/archive/2011/03/30/1999764.html
推荐博客：http://www.cnblogs.com/zxndgv/archive/2011/08/02/2125242.html
hdu 2952 Counting Sheep
poj 1160 Post Office
hdu 3480 Division
hdu 3516 Tree Construction
hdu 2829 Lawrence

图论

POJ综合题
https://blog.csdn.net/liuqiyao_01/article/details/8477827

并查集&最小生成树（学习区）

https://blog.csdn.net/liuqiyao_01/article/details/8797356
【HDU】
1213 How Many Tables 基础并查集★
1272 小希的迷宫基础并查集★
1325&&poj1308 Is It A Tree? 基础并查集★
1856 More is better 基础并查集★
1102 Constructing Roads 基础最小生成树★
1232 畅通工程基础并查集★
2120 Ice_cream’s world I 基础并查集★
2122 Ice_cream’s world III 基础最小生成树★
1233 还是畅通工程基础最小生成树★
1863 畅通工程基础最小生成树★
1875 畅通工程再续基础最小生成树★
1879 继续畅通工程基础最小生成树★
3371 Connect the Cities 简单最小生成树★
1301 Jungle Roads 基础最小生成树★
1162 Eddy’s picture 基础最小生成树★
1198 Farm Irrigation 基础最小生成树★
1598 find the most comfortable road 枚举+最小生成树★★解题报告
1811 Rank of Tetris 并查集+拓扑排序★★ 解题报告
3926 Hand in Hand 同构图★
3938 Portal 离线+并查集★★
2489 Minimal Ratio Tree dfs枚举组合情况+最小生成树★
4081 Qin Shi Huang’s National Road System 最小生成树+DFS★★
4126 Genghis Khan the Conqueror 枚举+最小生成树+DFS(难)★★★★
2860 并查集
2144 LCS+并查集
1829&&poj2492 A Bug’s Life 基础种类并查集★
1558 Segment set 计算几何+并查集★
3461 Code Lock 并查集(有点难想到)★★
3367 Pseudoforest 最大生成树★
2473 Junk-Mail Filter 并查集+设立虚父节点(马甲)★★
3172 Virtual Friends 带权并查集★
3635 Dragon Balls 带权并查集★
3047 Zjnu Stadium 带权并查集★
3038 How Many Answers Are Wrong 种类并查集★★
2818 Building Block 带权并查集★
3234 Exclusive-OR 异或并查集(难)★★★
2121 Ice_cream’s world II 最小树形图(要输出根有点恶心)★★
4009 Transfer water 最小树形图(模板题)★
3311 Dig The Wells 斯坦纳树(状压DP)(模板题)★★
4085 Peach Blossom Spring 斯坦纳树(状压DP)(有可能是森林…)★★★
4253 Two Famous Companies
4263 Red/Blue Spanning Tree
4313 Matrix [最大生成森林]
4424 Conquer a New Region [最大生成森林]
4509 湫湫系列故事——减肥记II [可以用并查集，区间合并]
【POJ】
1258 最经典的MST★
1789 Truck History 最小生成树★
1287 Networking 简单★
2349 Arctic Network 简单★
1611 The Suspects 并查集★
2377 kruskal★
2524 Ubiquitous Religions 并查集★
2236 Wireless Network 并查集+计算几何★ 解题报告
2560 Kruskal 并查集★
1861 Kruskal★
3625 prim★
1679 - The Unique MST(基础) 判断MST是否唯一★
3522 - Slim Span(基础) 求一颗生成树，让最大边最小边差值最小★
2485 Highways MST中的最长边★
2395 最小生成树的最长边★
1751 Highways 求出方案★
POJ-1182 食物链种类并查集★★
POJ 1456 Supermarket 贪心+区间合并★
POJ-1703 种类并查集★
POJ-1988 种类并查集★
POJ-1733 Parity game 种类并查集，先要离散化一下，不影响结果★
POJ-1417 True Liars(难) 并查集+DP 种类并查集★★
POJ-2912 Rochambeau(难) baidu的题,很不错…是食物链的加强版.判断裁判比较难想.★★★
POJ 2728 - Desert King(中等) 最优比率生成树★★
POJ 1639 - Picnic Planning(较难) 顶点度数有限制的最小生成树★★
POJ 3164 - Command Network(难) 最小树形图★★
poj3723好题!!! ★★
poj3228好好题!!! ★★
POJ-1984 Navigation Nightmare二维曼哈顿距离并查集.
【ZOJ】
ZOJ-3261 逆向并查集 ★★
ZOJ-3613 斯坦纳树

拓补排序（学习区）

https://blog.csdn.net/liuqiyao_01/article/details/8478726
【HDU】
1285确定比赛名次
2094产生冠军
2647Reward
3342Legal or Not
1811Rank of Tetris 拓扑+并查集
3231 Box Relations 三维拓扑
【POJ】
1094 Sorting It All Out Floyd+拓扑
2367 Genealogical tree
3660 Cow Contest
3687 Labeling Balls 神奇的拓扑
1128Frame Stacking DFS版拓扑
1270Following Orders 拓扑+回溯
1420Spreadsheet 模拟拓扑
2762Going from u to v or from v to u? 强连通+拓扑
3553 Task schedule
最短路&差分约束（学习区）
https://blog.csdn.net/liuqiyao_01/article/details/8797353

最短路

【HDU】
1548 A strange lift基础最短路(或bfs)★
2544 最短路基础最短路★
3790 最短路径问题基础最短路★
2066 一个人的旅行基础最短路(多源多汇,可以建立超级源点和终点)★
2112 HDU Today基础最短路★
1874 畅通工程续基础最短路★
1217 Arbitrage 货币交换 Floyd (或者 Bellman-Ford 判环)★
1245 Saving James Bond计算几何+最短路★
1317 XYZZY Bellman-Ford判环,有负权★
1535 Invitation Cards 有向图的来回最短路,(反向建图)★
1546 Idiomatic Phrases Game 最短路★
2680 Choose the best route 最短路★
2923 Einbahnstrasse最短路★
3339 In Action 最短路+背包★
2224 The shortest path双调旅行商问题★★
2807 The Shortest Path矩阵运算+最短路(floyd)★★
1595 find the longest of the shortest枚举+最短路(删掉任意一条边的最长最短路)★★
3986 Harry Potter and the Final Battle 枚举+最短路(删掉任意一条边的最长最短路)★★
1599 find the mincost routefloyd求最小环★
1839 Delay Constrained… 二分下限+最短路(带限制最短路)★★
3631 Shortest Path Floyd插点法★★
4114 Disney’s FastPass 最短路+二维状压DP(难)★★★
3832 Earth Hour 三点连通(斯坦纳树)★
3873 Invade the Mars Dij变体(好题!,带限制最短路)★★★
4063 Aircraft 几何构图+最短路★★★★
hdu4179 Difficult Routes dis[][]开二维状态的最短路(带限制最短路)★★
2145 zz’s Mysterious Present 反向建边. 最短路
3268 最短路
3143 最短路
1869 六度分离 Floyd最短路★
1385 Minimum Transport Cost 最短路+输出路径(输出字典序最小路径,有点恶心)★★
1224 free DIY Tour 最短路+输出路径★
1142 A Walk Through the Forest 最短路+记忆搜索★★
1596 find the safest road 乘积最小的最短路★
1598 find the most comfortable road二分速度差+最短路(带限制最短路)★★
2722 Here We Go(relians) Again最短路★
2962 Trucking 二分+最短路(带限制最短路)★★
1690 Bus System 最短路★
2433 Travel 删边+最短路之和(预处理桥边)★★★
2363 Cycling 二分+最短路(带限制最短路)★★
2377 Bus Pass 最短路(寻找一个点的最长最短路最小)★★
2833 WuKong 最短路+记忆化搜索(求两条最短路的最多公共点)★★
1688 Sightseeing最短次短路条数★★
3191 How Many Paths Are There 次短路条数★★
2482 Transit search最短路★★★
3768 Shopping 最短路+dfs(或最短路+状压DP)★★
3035 War 平面图最小割(建图麻烦)★★
3870 Catch the Theves 平面图最小割(建图麻烦)★★
3860 Circuit Board 平面图最小割(建图麻烦)★★
4308 Saving Princess claire_ 最短路构图
4034 Graph [Floyd应用]
4157 Slalom 计算几何+最短路
4280 Island Transport [抠图+平面图最小割]
4293 Groups [最长路]
4318 Power transmission
4360 As long as Binbin loves Sangsang
4370 0 or 1
4396 More lumber is required
【POJ】
1062 昂贵的聘礼竟然可以和最短路联系起来★★ 解题报告
1094 Sorting It All OutFloyd 判环+拓扑排序★
1125 Stockbroker Grapevine Floyd★
1135 Domino Effect 最短路,比较有意思★★
1161 Walls 最短路(图太恶心了)★★
1502 MPI Maelstrom Floyd★
1511 Invitation Cards 来回最短路★
1556 The Doors 计算几何+最短路★★
1724 ROADS 带限制的最短路,dis[][]开二维来记录信息(或广搜)★★
1734 Sightseeing trip floyd最小环路径★
1797 Heavy Transportation 二分枚举+最短路★
1847 Tram 简单最短路★
1860 Currency Exchange 货币兑换★
1949 Chores 反向建边,求最长路★★
2139 Six Degrees of Cowvin Bacon Floyd★
2240 Arbitrage 货币兑换★
2253 Frogger 二分+最短路★
2312 坦克大战 spfa最短路本质变形–>广搜★
2387 Til the Cows Come Home 基础最短路★
2394 Checking an Alibi 最短路★
2449 Remmarguts’ Date A*求第K短路★★
2457 Part Acquisition 最短路 (输出路径)★★
2472 106 miles to Chicago 乘积最短路(log一下,乘变加)★★
2502Subway
2570 Fiber Network floyd
3013 圣诞树
3037Skiing
3072 Robot
3114 Countries in War 强联通+最短路
3160 Father Christmas flymouse 强联通+最长路
3255 Roadblocks
3259 Wormholes （寻找负权回路）
3268 Silver Cow Party
3311 Hie with the Pie floyd+状压
3328 Cliff Climbing
3439 Server Relocation
3463 Sightseeing 次短路条数
3159
3521 Geometric Map 计算几何+最短路
3549 GSM phone 计算几何+最短路
3594 Escort of Dr. Who How
3613 Cow Relays 经过N条边的最短路 // floyd + 二分矩阵
3615 Cow Hurdles
3621 最优比率环
3635 full tank?
3660 传递闭包
3662 Telephone Lines
4046 Sightseeing
【SGU314】一道神级求前k短路。。。

差分约束

【HDU】
1384 Intervals 基础差分约束★
1529 Cashier Employment 神级差分约束★★★★
1531 King 差分约束★
1534 Schedule Problem 差分约束输出一组解★
3440 House Man 比较好的差分约束★★
3592 World Exhibition 简单★
3666 THE MATRIX PROBLEM 中等★★
4274 Spy’s Work [先处理出欧拉序列,然后就是差分约束了…]
【POJ】
1201 Intervals
1275 Cashier Employment
1364 King
1716 Integer Intervals
2949 Word Rings
2983 Is the Information Reliable?
3159
3169
3687

二分匹配（学习区）

https://blog.csdn.net/liuqiyao_01/article/details/8797349
【HDU】
1068Girls and Boys 最大匹配★
1150Machine Schedule 最小点覆盖★
1151Air Raid 最小路径覆盖★
1179Ollivanders 最大匹配★
1281棋盘游戏行列匹配+求关键点★★
149850 years, 50 colors 行列匹配★
1507Uncle Tom’s Inherited Land* 黑白染色+奇偶匹配(1X2的矩形覆盖)★
1528Card Game Cheater 最大匹配★
1845Jimmy’s Assignment 最大匹配(HK算法)★
2063过山车最大匹配★
2119Matrix 行列匹配
2444The Accomodation of Students 并查集分集合+最大匹配(好题!)★★
2768Cat vs. Dog 最大独立集★★
3360National Treasures 黑白染色+最小点覆盖★★
1045Fire Net 行列匹配变形★★
1350Taxi Cab Scheme 最小路径覆盖★
1960Taxi Cab Scheme 最小路径覆盖★
3118Arbiter 二分匹配本质(好题!)★★★
3729I’m Telling the Truth最大匹配+输出字典序最大的匹配情况★★
2389Rain on your Parade 最大匹配(HK算法)★★
1054Strategic Game 最小点覆盖★
2819Swap 行列匹配+输出解★★
1669 Jamie’s Contact Groups 二分+多重匹配★★
3605Escape 多重匹配★
3861The King’s Problem 强连通+最小路径覆盖★★
2236无题II 二分+二分匹配★★
1083Courses 最大匹配★
1526A Plug for UNIX 最大匹配★
2458Kindergarten 行列匹配★
4160Dolls 最大匹配★
4185Oil Skimming 黑白匹配★
2413Against Mammoths 二分+二分匹配★★
3468Treasure Hunting 最短路+二分匹配★★★
3517 Adopt or not 最大独立集★★★
3026Chinese Chess 二分匹配必须边★★★
【POJ】
1087A Plug for UNIX
1274 The Perfect Stall
1469COURSES
1486 Sorting Slides 二分图的必须边
1548Robots
1698Alice’s Chance
1719Shooting Contest
2060 Taxi Cab Scheme 最小路径覆盖
2112 Optimal Milking 二分+多重匹配
2226 Muddy Fields 行列的覆盖
2239 Selecting Courses
2289 Jamie’s Contact Groups 二分+多重匹配
2446 Chessboard
2536 Gopher II
2584T-Shirt Gumbo
2594 Treasure Exploration 可相交最小路径覆盖
2672Hotkeys
2724 Purifying Machine
3020 Antenna Placement
3041 Asteroids 简单行列匹配
3189Steady Cow Assignment 二分+多重匹配
3216 Repairing Company
3343 Against Mammoths
3692 Kindergarten
poj2771最大独立集

欧拉回路&哈密顿回路（待学习）

https://blog.csdn.net/liuqiyao_01/article/details/8479339
https://blog.csdn.net/liuqiyao_01/article/details/26964205

连通&LCA（学习区）

https://blog.csdn.net/liuqiyao_01/article/details/8478730

网络流（学习区）

https://blog.csdn.net/shahdza/article/details/7779537
【HDU】
2732 Leapin’ Lizards(较难) [最大流]
3338 Kakuro Extension(较难，好题) [最大流][数和]神奇最大流行进列出
2883 kebab(中等) [最大流]判断满流
3605 Escape(中等，好题) 最大流
3081 Marriage Match II(中等，好题) [二分最大流]+并查集
3277 Marriage Match III(中等，好题) [二分最大流]同上,多了拆点
3416 Marriage Match IV(中等，好题) [最大流]最短路+最大流
2485Destroying the bus stations [最大流]最短路+最大流 [已验证最大流解法是错的]
3468 Treasure Hunting(中等) 最大流+最短路
3998 Sequence(较难) [DP+最大流]最长上升子序列
4309 Seikimatsu Occult Tonneru(中等) [最大流]枚举状态+最大流
3472 HS BDC(难) [混合欧拉]
1533 Going Home(入门题) [费用流]
3488 Tour(基础) [费用流]圈
3435 A new Graph Game(基础) [费用流]圈
1853 Cyclic Tour(基础) [费用流]圈
2686 Matrix(基础) [费用流]
3376 Matrix Again(基础) [费用流]
3667 Transportation(中等) [费用流]拆边
3315 My Brute(中等，好题) 费用流
3395 Special Fish(中等，好题) 费用流
2448 Mining Station on the Sea(中等) 费用流
4067 Random Maze(难) [费用流]
3947 River Problem(难) [费用流]神奇费用流,流量不等式建图
4406 GPA [好题] [官方题解为所谓的上下界费用流]
4411 Arrest [好题] [官方题解为所谓的上下界费用流]
3046 Pleasant sheep and big big wolf(入门题) [最小割]
1565 方格取数(1)(基础) [最小割]黑白染色
1569 方格取数(2)(基础) [最小割]黑白染色
3820 Golden Eggs(较难，好题) [最小割]方格加强
3491 Thieves(中等) [最小割]最小点割集
3657 Game(中等) [最小割]最大点权独立集
3313 Key Vertex(中等) [最小割]
3251 Being a Hero(中等) [最小割]
3452 Bonsai(基础) [最小割]一颗带边权的树,最小割求树根和叶子结点不连通
3987 Harry Potter and the Forbidden Forest(较难，好题) [最小割]最小割的情况下,求最少需要割掉多少条边.
2435 There is a war(较难，好题) [最小割]打造无敌桥
3917 Road constructions(中等) [最大权闭包]最大获利
3879 Base Station(中等) [最大权闭包]最大获利
3061 Battle(中等) [最大权闭包]最大获利
3996 Gold Mine(中等) [最大权闭包]最大获利
4307 Matrix(较难，好题) [最小割][项目分配问题]
4265 Science! (较难)
4289 Control(中等) [最小点权覆盖]
4292 Food(基础) [最大流]
4322 Candy(难) [好题][最大流]
【POJ】
二分匹配能做的题目（拿来玩最大流的模板用吧。。。）：
1087 A Plug for UNIX 最大流
1274 The Perfect Stall 最大流
1325 Machine Schedule 最大流
1698 Alice’s Chance 最大流
2239 Selecting Courses 最大流
2446 Chessboard 最大流好题啊
2536 Gopher II 最大流
2771 Guardian of Decency [最大流]二分匹配最大独立集
3041 Asteroids 最大流
2584 T-Shirt Gumbo 最大流
3189 Steady Cow Assignment 二分最大流
1149 PIGS(较难) [最大流] 绝对经典的构图题
1273 Drainage Ditches(入门题) [最大流]
1459 Power Network(入门题) [最大流]
3281 Dining(入门题) [最大流]
2112 Optimal Milking(中等) [二分最大流]
2289 Jamie’s Contact Groups(中等) [二分最大流]
2391 Ombrophobic Bovines(中等) [二分最大流]
2455 Secret Milking Machine(中等) [二分最大流]
3228 Gold Transportation(中等) 二分最大流
2699 The Maximum Number of Strong Kings(较难) [枚举人数 + 最大流]
3498 March of the Penguins(中等) [最大流]枚举汇点,满足点容量限制的网络流
1637 Sightseeing tour(难) [混合欧拉]
2135 Farm Tour(基础) [费用流] (来回最短路)
2175 Evacuation Plan(较难) [费用流] 消圈
2195 Going Home(入门题) [费用流]
2516 Minimum Cost(中等) [费用流]
3422 Kaka’s Matrix Travels(中等) [费用流]拆点
3680 Intervals(较难，好题) [费用流]经典,费用流+离散化
3686 The Windy’s(难，好题) 费用流
3762 The Bonus Salary!(较难) [费用流]
1815 Friendship(中等) [最小割]最小点割集
1966 Cable TV Network(中等) [最小割]最小点割集
2125 Destroying The Graph(难) [最小割]最小点权覆盖
3084 Panic Room(中等，好题) [最小割]边连通度
3204 Ikki’s Story I - Road Reconstruction(中等) [最小割]求关键边
3308 Paratroopers(较难) [最小割]乘积取对数,最小点权覆盖
3436 ACM Computer Factory [最小割]收集流,残留搜集找边
3469 Dual Core CPU(中等) [最小割]项目分配问题
2987 Firing(较难，好题) [最大权闭包]
3155 Hard Life(很挑战一题) [最大密度子图]
【其他OJ】
LightOJ 上面已经有分类了,所以自己可以在上面找网络流的题目切吧。。。

zoj3348 Schedule(基础，好题) [最大流]已经比了几场,还有几场没比.问DD能不能取得冠军
zoj2760 How Many Shortest Path(基础) [最大流]不相交最短路径数
zoj3460 Missile(中等) [最大流]按不同时间将每个点拆点,二分时间,判断是否是完美匹配.
zoj3362 Beer Problem(中等) [费用流]最大费用流,每次增广.直到费用归本时,break;
zoj2532 Internship(中等) [最小割]增加哪些边的流量,可以增大最大流.(求关键割边)
ZOJ2587 Unique Attack(中等) 最小割
ZOJ2539 Energy Minimization(较难，好题) [最小割]项目分配问题
ZOJ2071 Technology Trader(较难，好题) [最大权闭包]输出选择方案
ZOJ2332 Gems(中等) [最大流]

SGU326 Perspective (构图题，类似于 WHU 1124)
SGU438 The Glorious Karlutka River =) (按时间拆点)
SGU242 Student’s Morning (输出一组解)
SGU185 Two shortest (Dijkstra 预处理，两次增广，必须用邻接阵实现，否则 MLE)

HOJ2816 Power Line
HOJ2634 How to earn more
HOJ2811 Earthquake Damage (最小点割集)
HOJ2715 Matrix3
HOJ2739 The Chinese Postman Problem
HOJ2543 Stone IV

WHU1124 Football Coach (构图题)
JOJ2453 Candy (构图题)
TJU2944 Mussy Paper (最大权闭合子图)
BUAA1032 Destroying a Painting
BASHU2445(绝对经典的费用流) 餐巾问题

SPOJ 839 Optimal Marks (将异或操作转化为对每一位求最小割)
Spoj660：http://www.spoj.pl/problems/QUEST4/
Spoj377：http://www.spoj.pl/problems/TAXI/

[UVA]

753 , 820 , 10330 , 10735
11248 [最大流]先求起点到终点的最大流,然后在残留网络中,求起点到每个点的最大流,以及每个点到终点的最大流.然后枚举每条边增加容量能否满足题意.

[TC]:
Single Round Match 200 Round 1 – Division I, Level Three
Single Round Match 236 Round 1 – Division I, Level Three
Single Round Match 399 Round 1 – Division I, Level Three
2003 TCO Semifinal Round 4 – Division I, Level Three
2004 TCCC Championship Round – Division I, Level Three
2005 TCO Sponsor Track Round 3 – Division I, Level One

[RQNOJ]
306 破坏石油运输系统问题
338 [NOI08]志愿者招募
529 [NOI09]植物大战僵尸
556 [NOI06]最大获利

606 [NOI2010]海拔
【上下界网络流】
ZOJ 2314 可行流
Zoj 3229 最大流
zoj 1994 可行流

Pku 2396 可行流
poj 2594 最小流
Hdu3157 最小流
Sgu176 最小流
hust1342 最小流
【无向图最小割】
hdu3691
hdu3002
poj2914
poj1966
zoj2753
2-SAT（待学习）
https://blog.csdn.net/liuqiyao_01/article/details/8797336
KM匹配（待学习）
https://blog.csdn.net/liuqiyao_01/article/details/8797346
Dancing Links（待学习）
https://blog.csdn.net/liuqiyao_01/article/details/8478711
一般图匹配（待学习）
https://blog.csdn.net/liuqiyao_01/article/details/26963579
线段树
https://blog.csdn.net/trapper_c/article/details/51919980
练习区（单点更新-成段更新）
hdu1754
hdu1394
hdu2795
poj2828
poj2886
hdu4288
CodeforcesBeta Round #19 D
poj2481
hdu3950
hdu4521
CodeforcesBeta Round #99 (Div. 1) C
hdu 4605
URAL 1989 Subpalindromes
hdu 4777
hdu1698
poj3468
poj2528
poj1436
poj2991
uestc1425
uestc1546
CodeforcesRound #136 (Div. 2) D
Uva 12436
CodeforcesRound #169 (Div. 2) E
CodeforcesBeta Round #35 (Div. 2) E
Zoj3299
fzu2105
hdu 4533
URAL 1855
hdu 4578
hdu 4455
hdu 4614
hdu 4747
zoj 3724
cf343D
URAL 1977
学习区（区间合并-扫描线-其他）
hdu3397
hdu2871
hdu1540
CodeforcesBeta Round #43 D
hdu1828& poj 1177（同一题）
hdu1255
hdu 3642
poj2482
poj2464
hdu3255
uva 11983
hdu4052
uestc1525
hdu4419
zoj 3521
zoj 3525
hdu3954
hdu4027
hdu3333
hdu3016
hdu3340
ZOJ3511
UESTC1558
spojGSS21557
poj3162
hdu4358
hdu4267
hdu4417
UVALive4730
CodeforcesRound #163 (Div. 2) E
hdu 4638
hdu 4630
字符串算法
KMP
https://blog.csdn.net/chenguolinblog/article/details/16857765
（已完结）
字典树
https://blog.csdn.net/chenguolinblog/article/details/13625389
AC自动机
https://blog.csdn.net/liuqiyao_01/article/details/8798241
后缀数组
计算几何（模板库训练）
https://blog.csdn.net/feizaoSYUACM/article/details/54835327
https://blog.csdn.net/chm517/article/details/44892713
https://blog.csdn.net/liuqiyao_01/article/details/8750742
https://blog.csdn.net/liuqiyao_01/article/details/26964261
金银牌题库
HDU-5859-2016多校10-金牌题
HDU-5864-2016多校10-银牌题
HDU-5865-2016多校10-金牌题
HDU-5866-2016多校10-银牌题
牛客网2018暑期多校5B-div-银
牛客网2018暑期多校5C-grf-金
牛客网2018暑期多校5D-inv-金
牛客网2018暑期多校5H-subseq-银
牛客网2018暑期多校5I-vcd-银
牛客网2018暑期多校6B-Endless Pallet-金
牛客网2018暑期多校6E- Charmander-金
牛客网2018暑期多校6H- Eevee-金
牛客网2018暑期多校6F- Squirtle-银
牛客网2018暑期多校6G- Pikachu-银
2018百度之星程序设计大赛资格赛-1004-点集划分-金
HDU-6387-2018杭电多校10-1002-银牌题
HDU-6388-2018杭电多校10-1003-金牌题
HDU-6389-2018杭电多校10-1004-金牌题
HDU-6391-2018杭电多校10-1006-金牌题
HDU-6392-2018杭电多校10-1007-金牌题
金牌题（无明显前置）题集
金牌题-前置:无
2018杭电暑期多校4H-HDU6339-Eat Cards,Have Fun
【题意】
【TAG】
【题解】
【代码】
金牌题-前置：无
牛客网2018暑期多校4B-Interval Revisited
【题意】
【TAG】区间操作线段树优化
【题解】
【代码】
金牌题-前置：无
2018杭电暑期多校1F-HDU6303-Period String
【题意】
【TAG】字符串
【题解】
【代码】
金牌题-前置：无
2018杭电暑期多校3H-HDU6326-Monstor Hunter
【题意】
【TAG】
【题解】
【代码】
金牌题-前置：无
2018杭电暑期多校2I-HDU6317-Segment
【题意】
【TAG】动态规划
【题解】
【代码】
金牌题-前置：无
2018杭电暑期多校1E-HDU6302-Maximum Weighted Matching
【题意】
【TAG】图论 DP
【题解】
【代码】
金牌题-前置：无
2018杭电暑期多校2A-6309-Absolute
【题意】
【TAG】数学
【题解】
【代码】
金牌题-前置：无
2018杭电暑期多校3E-HDU6323-Find The Submatrix
【题意】
【TAG】动态规划矩阵
【题解】
【代码】
金牌题-前置：未知
牛客网2018暑期多校3F-Sum of Digits
【题意】
【TAG】
金牌题-前置：未知
牛客网2018暑期多校3G-Coloring Trees
【题意】
【TAG】
金牌题-前置：未知
2018杭电暑期多校1I-HDU6306-Lyndon Substring
【题意】
【题解】
【代码】
金牌题-前置：未知
2018杭电暑期多校1J-HDU6307-Turn off the light
【题意】
【题解】
【代码】
金牌题-前置：未知
牛客网2018暑期多校3B-Expected Number of Nodes
【题意】
【TAG】
金牌题-前置：未知
牛客网2018暑期多校3D-Encrypted String Matching
【题意】
【TAG】
金牌题-前置：无
2018杭电暑期多校4C-HDU6334-Problems on a Tree
【题意】
【TAG】并查集
【题解】
【代码】
金牌题-前置：数论银牌题
2018杭电暑期多校4A-HDU6332-Integers Exhibition
【题意】
【TAG】数论
【题解】
【代码】
银牌题-前置：笛卡尔树
2018杭电暑期多校1H-HDU6305-RMQ Similar Sequence
【题意】
【TAG】
【题解】
【代码】
金牌题-前置：树型DP
牛客网2018暑期多校2E-tree
【TAG】动态规划
金牌题-前置：网络流
牛客网2018暑期多校2F-trade
【TAG】
金牌题-前置：凸包
牛客网2018暑期多校2C-message
【题意】
【TAG】凸包
金牌题-前置：可持久化Treap
2018杭电暑期多校4F-HDU6337-Travel Through Time
【题意】
【TAG】可持久化
【题解】
【代码】
金牌题-前置：Steiner树/最小边数Dreyfus-Wagner算法
牛客网2018暑期多校1G-Steiner tree
【TAG】数据结构树
金牌题-前置：斜率优化/李超树
牛客网2018暑期多校1H-Longest Path
【TAG】最短路斜率优化
金牌-前置：回文树/回文自动机/回文后缀
2018杭电暑期多校3B-Cut the String-HDU6320
【题意】
【TAG】字符串回文串区间查询金牌题欧几里得算法
【题解】
【代码】
金牌：前置：Manacher算法/后缀数组
牛客网2018暑期多校4H-Double Palindrome
【题意】
【TAG】回文串字符串
【题解】
【代码】

第四部分

模板库

附录A 题目索引

附录B 常用平台

附录C 在线OJ

国内

ZJUT 浙江工业
ZJU 浙江大学
POJ 北京大学
TJU 天津大学
厦门大学
FZU 福州大学
HUST 华中科技
宁波理工
汕头大学
中国科大
西南科大
暨南大学
中山大学
福建师范
哈工业大
四川大学
哈工程大
武汉大学
同济大学
南开大学
湖南大学
上海大学
兰州大学
宁波大学
HDU 杭州电子科技大学
ECNUOJ 华东师范大学
浙江师范大学（ZJNU）
高效信息学在线判题系统(一个中学生做的)
91信息学
在线评测系统(面向中学生

国外

西班牙Valladolid大学
瓦拉杜利德大学（UVA）
俄罗斯Ural立大学
UsacoGate
Saratov State University
EL Judge(MIPT)
SPOJ
KRSU
ICPC

参考文献

【1】https://www.cnblogs.com/lenmom/p/7988635.html
【2】https://blog.csdn.net/swpu_yx32/article/details/52858684
【3】https://blog.csdn.net/yanggangclcsdn/article/details/49704089
【4】https://www.cnblogs.com/keshuqi/p/6257642.html
【5】http://www.sgi.com/tech/stl/Rope.html
【6】https://blog.csdn.net/Sirius_han/article/details/82313029
【7】https://blog.csdn.net/huzecong/article/details/8576908
【8】https://blog.csdn.net/acmore_xiong/article/details/52270748
【9】https://blog.csdn.net/f_zyj/article/details/51473493
【10】https://www.cnblogs.com/HarryGuo2012/p/4728243.html
【11】https://blog.csdn.net/yoer77/article/details/70943462
【12】https://blog.csdn.net/lzc504603913/article/details/82290576
【13】https://blog.csdn.net/qq_35392050/article/details/60779183
【14】https://www.bilibili.com/video/av3246487?from=search&seid=8616183992466782178
【15】https://www.bilibili.com/video/av25326779?from=search&seid=2767747169022162614
【16】https://blog.csdn.net/trapper_c/article/details/51919980
【17】https://blog.csdn.net/u013761036/article/details/46363605
【18】https://www.cnblogs.com/CsOH/p/5904430.html
【19】https://blog.csdn.net/thinfatty/article/details/72581276
【20】https://www.myblog.link/2016/01/26/MO-s-Algorithm/
【21】https://www.bilibili.com/video/av18735440?from=search&seid=1530520915414646384
【22】https://blog.csdn.net/acdreamers/article/details/8236942
【23】https://oeis.org/
【24】https://blog.csdn.net/u012061345/article/details/52224623
【25】https://www.cnblogs.com/ACMLCZH/p/8022502.html
【26】

ACM比赛经验、刷题记录及模板库总结（更新中）

前言

第一部分 经验分享及感受

第二部分 刷题记录

一、基础算法&程序语言

C++ string类

new&delete

创建并释放一维数组

创建并释放二维数组

STL

map

vector

next_permutation

优先队列（priority_queue）

C++11

auto

for循环

断言（assert）

数据对拍（输入输出重定向-freopen）

宏定义

大数模板（C/C++）

JAVA

BigDecimal

可持久化平衡树（C++ Pb_ds库 Rope）

bzoj1269 文本编辑器

牛客网2018暑期多校第3场-C（可持久化平衡树）

基础题

牛客网2018暑期多校第4场-F-Beautiful Garden-签到题

枚举

2018ICPC南京站网络预选赛- The writing on the wall

2018百度之星程序设计大赛资格赛1001-调查问卷

贪心

HDU-6385-rect

模拟

2018ICPC南京站网络预选赛-GDY

EOJ-3628- A Simple Convolution

牛客网2018暑期多校6A-Singing Contest

HDU-6330-Visual Cube-签到题

HDU-6342- Expression in Memories-签到题

搜索

深度优先搜索（DFS）

HDU-6341-Let Sudoku Rotate

HDU-6351-Beautiful Now

广度优先搜索（BFS）

二分

HDU-6383-p1m2

构造

ECNU ICPC/CCPC Trial Round #1-K-Kblack Playing Cards

ECNU ICPC/CCPC Trial Round #1-I-Intersections

EOJ-3630-Bad Queen

HDU-6300-Triangle Partion

曼哈顿距离最小生成树

输入输出外挂

题库

二、综合题（现场题）

题库

三、动态规划

递推

HDU-2050-折线分割平面

基础动态规划

最大连续子段和

HDU-1003

LIS（最长上升子序列）

单调栈优化

HDU-1087

LCIS（最长上升公共子序列）

HDU-1503-Advanced Fruits

HDU-1159-LCIS模板题

背包问题

0-1背包

HDU-2602-Bone Collector

完全背包

HDU-1114-Piggy Bank

多重背包

数位DP

HDU-2089-不要62

状态压缩DP

2018ICPC南京站网络预选赛-AC Challenge

概率DP

牛客网-第1场-E-Removal-铜牌

第一部分经验分享及感受

第二部分刷题记录