GACNN:利用遗传算法训练深度卷积神经网络
GACNN:利用遗传算法训练深度卷积神经网络
- 引言
- 背景
- 卷积神经网络
- 遗传算法
- 研究方法
- 稳态遗传算法
- 世代遗传算法
- 精英遗传算法
- 评估结果
- 结论
- 代码实现与结果
原文地址:GACNN: TRAINING DEEP CONVOLUTIONAL NEURAL NETWORKS WITH GENETIC ALGORITHM
这篇论文是《数据挖掘与应用》课程的期中汇报作业,借此机会记录下论文笔记与代码实现。
引言
目前,在用遗传算法训练卷积神经网络的领域,大多数工作在一些重要方面尚有缺陷,例如缺少不同深度网络与数据集之间的对比,缺乏对遗传算法参数的探索,在大规模网络中失效,缺乏对不同遗传算法方案的探索等。
针对以上问题,本文提出了一些新思路,主要贡献如下:
- 介绍Accordion染色体结构(Accordion Chromosome Structure):相比传统染色体编码方式规模更小、运算更快、进化更有效。
- 提出全新遗传算子(Genetic Operator)。
- 介绍三个创新性的遗传算法方案:稳态(Steady-State)、世代(Generational)、精英(Elitism)。
背景
卷积神经网络
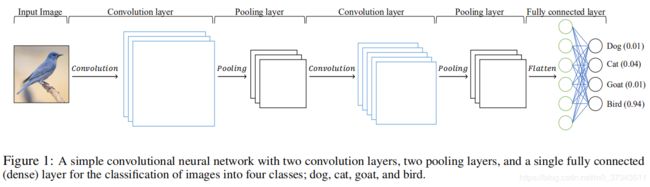
近年来,卷积神经网络(Convolutional Neural Network, CNN)在计算机视觉、语音识别等领域被认为是最有效和流行的工具之一。传统的人工神经网络(Artificial Neural Network, ANN)由于只用原生数据而不能检测到某些重要特征,因此无法高效处理大规模问题,而CNN则提供了一种解决方法。Figure 1展示了一个简单的CNN。
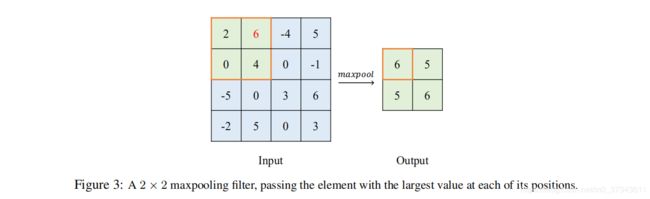
- 特征提取(Feature Extraction) :这部分利用卷积层(Convolution Layer)、池化层(Pooling Layer)检测图片中的某些特征,例如边缘、形状等,以达到降维的目的。在卷积层中,一个过滤器(Filter)与对应输入值相乘后求和,再通过激活函数得到输出。然后,这个过滤器遍历整张图片,以提取其重要特征,如Figure 2所示。接下来,池化层将进一步降低图片维度,如Figure 3所示。以上的过滤与池化过程将一直重复,直到图片维度降低到可接受的程度。下一步则交给分类部分来分类降维后的图片。
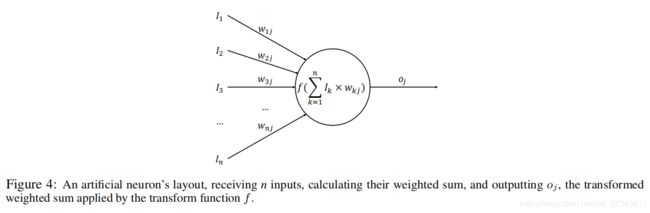
- 分类(Classification):这部分是一个简单的多层感知机(Multilayer Perceptron, MLP),如Figure 4所示。
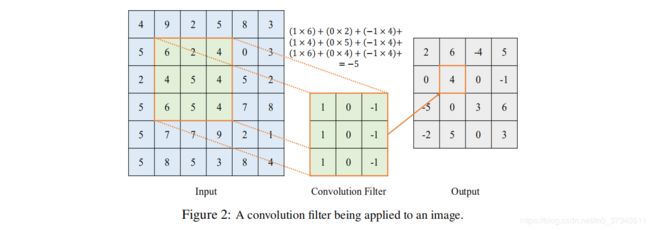
总结下来,CNN的训练过程就是通过改变其参数,尤其是过滤器与权重的值,来最小化损失函数。
遗传算法
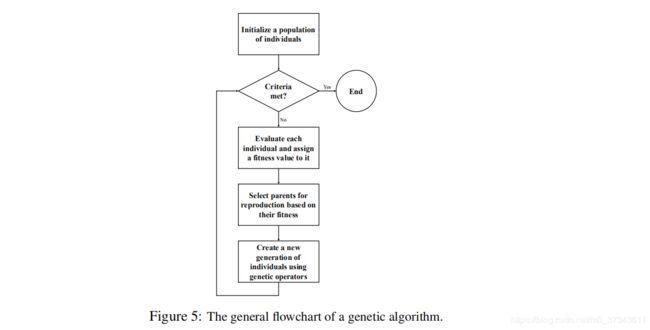
遗传算法(Genetic Algorithm, GA)基于达尔文的进化论,是一种由自然选择启发的,可用于解决有约束与无约束优化问题的全局优化方法。在每次迭代过程中,GA从当前种群中选择“最好”的个体作为双亲来产生子代,以使种群朝最优解“进化”。GA的流程图如Figure 5所示。
- 初始化(Initialization):初始种群包括一系列随机产生的可能解。
- 评估(Evaluation):通过适应度函数(FItness Function),即通常情况下的目标函数计算每个成员的适应度。
- 选择(Selection):在每次世代交替时,一般来说适应度更高的个体会被选择来产生下一代。常见的选择策略有轮盘赌选择(Roulette-wheel Selection)、锦标赛选择(Tournament Selection)和随机全局采样(Stochastic Universal Sampling)。
- 遗传算子(Genetic Operators):将交叉(Crossover)、变异(Mutation)等遗传算子应用到被选择的个体上来产生下一代。经过该步骤后,总体来说,种群的平均适应度会增加。
- 终止(Termination):若找到一个满足最小标准的解,达到设定的世代数或适应度达到稳定水平等条件,则终止。
研究方法
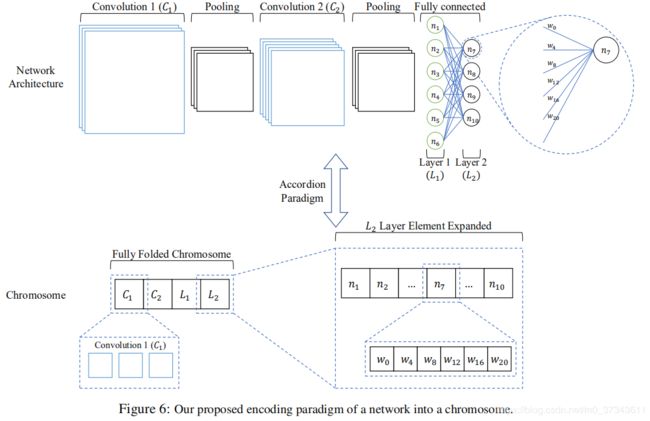
利用GA训练CNN的挑战在于如何将网络映射到染色体上。传统的编码模式将每个网络参数作为染色体的一个元素,而在大规模网络中,这种编码模式将使得染色体结构过于庞大,导致遗传算子失效等问题。一个解决方法是将每个卷积层与全连接层看作一个整体作为染色体的一个元素,即每个染色体元素要么包含一个层的所有连接权重,要么包含一个过滤器的所有值。这种编码模式大大缩减了染色体结构,使其具有更快的运算时间,更快的收敛速度以及更高的正确率。如Figure 6所示。
关于适应度,本文使用分类交叉熵(Categorical Cross-entropy)。
以上研究方法可以通过三个GA方案进行:
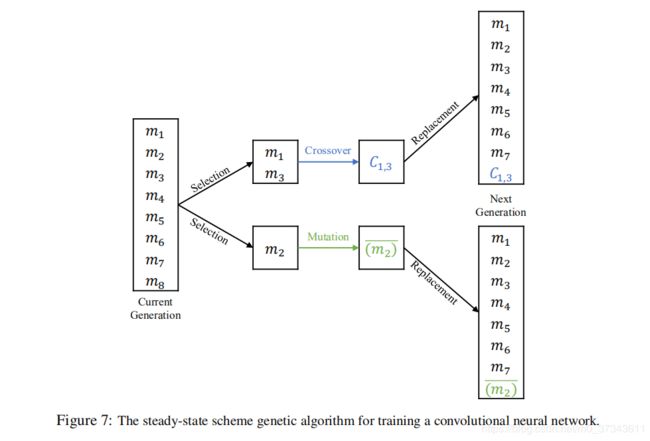
- 稳态(Steady-State):子代代替“最差”的成员。
- 世代(Generational):子代代替整个种群。
- 精英(Elitism):保留“最好”的成员。
稳态遗传算法
- 初始化(Initialization):利用Keras初始化数量为pop_size的种群,每个网络的过滤器与连接权重从均值为0的截尾正态分布中随机产生,该过程可利用Keras的Glorot normal initializer完成。
- 评估(Evaluation):每个网络的表现基于Keras的model.evaluate()函数给出,该步骤在multiprocess的使用下有更快的运行时间。
- 适应度赋值(Fitness Assignment):此处我们使用每个网络的正确率作为适应度。
- 选择(Selection):我们使用最有名的选择策略:适应度比率选择(Fitness Proportional Selection),也被称为轮盘赌选择(Roulette-wheel Selection),即一个网络的适应度越高,其被选择的可能性就更大。该过程的参数如Table 1所示。
交叉(crossover)算子由双亲产生一个子代,变异(mutation)算子由一个父代产生一个子代。如果选择变异,那么先从[0, 1]上的均匀分布中产生一个随机数并与 P i P_i Pi比较,如果小于 P i P_i Pi,那么第 i i i个个体就会被选择。如果选择交叉,那么以上过程将进行两次,选择两个个体。 - 交叉(Crossover):对卷积层,该过程随机选择双亲的其中一个,并将对应的过滤器拷贝到子代。对全连接层的每一个神经元,该过程仍然随机选择双亲的其中一个,并将所有权重拷贝到子代。如Figure 8所示。
- 变异(Mutation):如果被选择的是卷积层,那么其中的每一个值由均值为该值,标准差为0.5的高斯噪音代替。如果是神经元,则将每一个权重加上一个来自初始分布的随机数。如Figure 9所示。
- 代替(Replacement):新产生的子代将取代最不适应的个体,pop_size保持不变。



以上流程从第2步开始重复,直到达到某个标准(如世代数、正确率等)。这种方案将保留“最好”的个体,并且只有在更好的个体出现时才改变种群。这会使得其稳定但缓慢地收敛到全局最优解。在选择的过程中,适应度更高的个体将更频繁地被选择。
为简单起见,我们不考虑权重中的bias和dropout层。
世代遗传算法
该算法的【1. 初始化、2. 评估、3. 适应度赋值】步骤与稳态遗传算法相同,不再赘述。
4. 选择:每个个体被选择的概率的计算方式与稳态遗传算法相同。接下来,一些个体将被选择进入交配池(Mating Pool),交配池大小与种群大小一致,这意味着一些个体将被选择多于一次。下一步是将交配池中的个体随机配对。
5. 交叉:每一对产生两个互补的子代,产生过程与稳态遗传算法相同。这将产生一群数量为pop_size的子代。
6. 变异:基于变异比例(mutation_ratio),子代中的一些个体将被随机选择经历变异,变异过程与稳态遗传算法相同,变异后的个体将取代自身。
7. 代替:新一代将完全取代上一代,标志着一次迭代的完成。
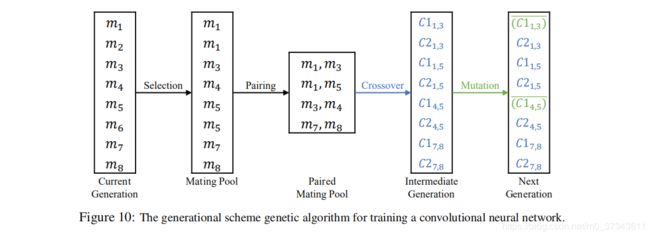
该算法的流程如Figure 10所示。
精英遗传算法
该算法的【1. 初始化、2. 评估、3. 适应度赋值】步骤与稳态遗传算法和世代遗传算法相同,不再赘述。

4. 选择:与世代遗传算法不同的是,交配池大小与种群大小不相同。这是因为最适应的个体(如前10个),即精英,将直接进入下一代。此外,交配池中的个体将不会被随机配对,而是随机选择双亲通过交叉产生一个子代,然后将双亲放回交配池。
5. 交叉:双亲使用与稳态遗传算法相同的交叉算子产生一个子代,直到子代填满下一代种群。
6. 变异:与世代遗传算法相同,一些子代将经历变异。
7. 代替:新子代与精英共同组成了下一代种群,标志着一次迭代的完成。
该算法的流程如Figure 11所示。
容易发现,这种算法将可能产生前两种算法的最好结果。一方面,稳态遗传算法收敛稳定但是缓慢;另一方面,世代遗传算法进化得更快,但达到最优解的过程更加震荡。我们希望通过结合这两种算法能产生最好的结果。
评估结果
首先,我们在MNIST和CIFAR10数据集上进行评估,Table 2与Table 3展示了网络结构。MNIST的网络结构是自定义的,而CIFAR10的网络结构是著名的LeNet网络。
对于稳态遗传算法,有70%的可能性选择交叉,30%的可能性选择变异。变异比例(mutation_ratio)设为10%.
对于世代遗传算法,变异概率设为20%,变异比例设为10%.
对于精英遗传算法,前10个最适应的个体直接进入下一代。选择20个个体进入交配池,产生剩下的90个子代。
对于MNIST数据集,70000张图片用于训练和验证,10000张图片用于测试。对于CIFAR10数据集,50000张图片用于训练和验证,10000张图片用于测试。batch_size设为32.
值得注意的是,对于每个网络,我们初始化一个种群,再用不同的算法进化,这会使得初始正确率相等。当与反向传播(Back Propagation,BP)算法比较时,初始化种群中适应度最高的个体将被选择用BP算法训练。
Accordion编码与传统编码在两个数据集,三种遗传算法上的表现如Figure 12-14所示。
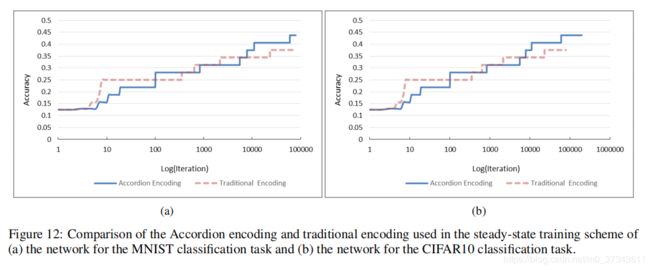

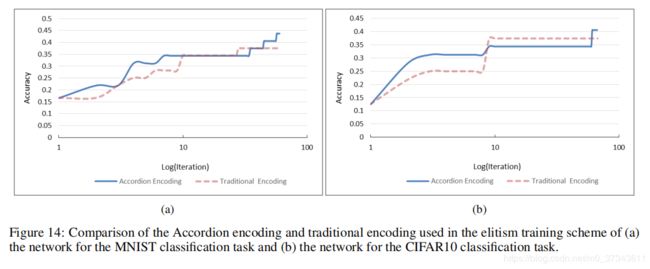
Figure 15展示了在Accordion编码方式下,三种遗传算法在两个数据集上的表现的对比。
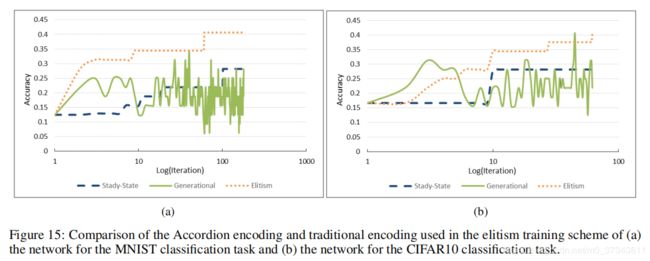
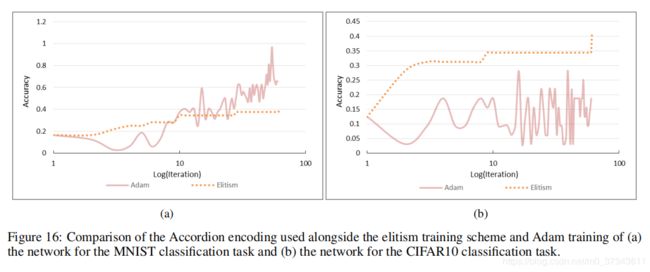
Figure 16展示了表现最好的精英算法与传统Adam算法在两个数据集上的表现的对比。
结论
本文提出的全新的编码方式极大缩小了染色体大小,并且表现好于传统编码方式。通过对三种遗传算法收敛性与正确率的分析,本文推断出稳态算法收敛稳定但是缓慢;世代算法进化得更快,但达到最优解的过程更加震荡;精英算法收敛得更快也更稳定。
代码实现与结果
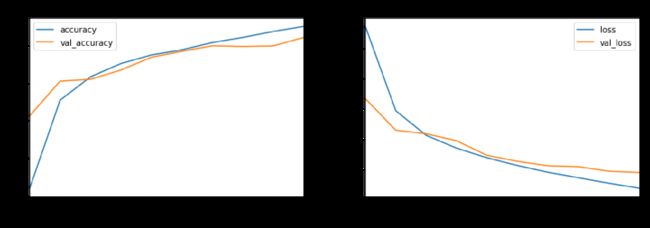
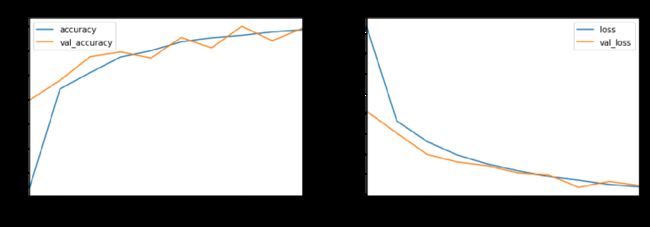
三种遗传算法在CIFAR10数据集上的表现如下。