数据结构 排序
知识要点:
1、插入排序法(含折半插入排序法)、选择排序法、泡排序法(冒泡排序)、快速排序法、
堆积排序法(堆排序)、归并排序、基数排序等排序方法排序的原理、规律和特点;
2、各种排序算法的时空复杂度的简单分析。
排序的稳定性:排序后不改变原序列中相同元素的相对顺序,则此排序方法是稳定的,反之是不稳定的;
一般情况下,排序的稳定性与其效率成反比;
插入排序法(含折半插入排序法):
算法思想:每次将一个待排序的数据,跟前面已经有序的序列的数字一一比较找到自己合适的位置,插入到序列中,直到全部数
据插入完成。(找位置+挪位置)
void InsertSort(int data[],int n){
int j;
for(int i=1;i0;j--){
if(data[j-1]>t){
data[j]=data[j-1];
//元素后移;
}
else{
break;
//找到插入位置
}
}
data[j]=t;
}
} 折半插入排序和插入排序的时间复杂度相同,两者的区别在于比较的次数不同 ,对于插入排序最坏比较次数为n(n-1)/2,即平均
比较次数为n^2数量级;而对于折半插入排序,采用折半查找的方式查找元素的插入位置,平均比较次数为nlogn数量级;两者的
就在于确定元素插入位置的比较次数;
时间复杂度:O(n^2); 稳定性:稳定;
选择排序法:
算法思想: 数组分成有序区和无序区,初始时整个数组都是无序区,然后每次从无序区选一个最小的元素直接放到有序区的最
后,直到整个数组变有序区。每一次选择待排序列中的最小(最大)的值放入有序序列为尾部;
void SelectSort(int data[],int n){
for(int i=0;i时间复杂度:O(n^2); 稳定性:不稳定/稳定;(基于交换的是不稳定的,基于插入的是稳定的)
泡排序法(冒泡排序):
算法思想:依次比较相邻的两个数,将小数放在前面,大数放在后面,主观上看就是大数依次排到末尾位置;
void BubbleSort(int data[],int n){
for(int i=0;i时间复杂度:O(n^2); 稳定性:稳定;
快速排序法:
算法思想:选取一个基准,从后往前找比此数值大(小)的元素的位置,从前往后找比此数值小(大)的元素的位置
经过每一次排序都可将数值划分为两部分(比基准大和小的两部分),在采用递归的方式分别将基准两侧的待排序列
进行同样的操作,直至各个待排序列均有序;
void QuickSort(int data[],int start,int end){
int t=data[start];//比较基准
if(startt){
break;
}
i++;
}
if(i 在快速排序中如果每次选择的中枢值可以将待排子表划分为长度近似相等的子表是,排序的速度是最快的,当元素本身有序时
则速度是最慢的,快速排序的递归树最高为n,最小为nlog2n;
一道例题:求下列数据经理一次快排后的序列(排序序列由小到大);
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| data | 49 | 38 | 65 | 97 | 76 | 13 | 27 | 49 |
起始基准为49,i=0,j=7,从后向前找第一个比49小的数;当j=6时此时满足要求,data[0]=data[6]=27,i=1,j=6;
在从前往后找第一个比49大的数,当i=2时满足要求,data[6]=data[2]=65,i=2,j=5;
重复以上步骤直至i与j相等为止;则最终一次快排序列为
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| data | 27 | 38 | 13 | 49 | 76 | 97 | 65 | 49 |
时间复杂度:最优时间复杂度O(nlog2n),最坏时间复杂度O(n^2); 排序的稳定性:不稳定;
堆积排序法(堆排序):
大根堆(根结点的关键字的值不小于其孩子结点的值)
小根堆(根结点的关键字的值不大于其孩子结点的值)
堆的结构形式为完全二叉树,可采用一维数组的方式进行存取,父节点对应数组下标为i,其左右孩子结点如果有分别
对应数组下标2i+1和2i+2;(最后一个非叶子结点为(n/2)-1,n为结点的个数)
堆排序就是交换根结点与最后一个结点,并重新调整堆的过程,对于大根堆全部序列"删除"完后,其数组有小到大
对于小根堆其全部序列“删除”完后,其数组由大到小;
void Swap(int *a,int *b){
int t=*a;
*a=*b;
*b=t;//交换元素的值
}
void AdjustHeap(int data[],int loc,int n){
//调整为大根堆
if(loc<=(n/2)-1){
int maxloc=2*loc+1;//非叶子结点一定有左孩子
if(2*loc+2=0;i--){
AdjustHeap(data,i,n);
//叶子结点一定都满足堆定义,从第一个非叶子
//结点开始调整堆,第一个非叶子结点为(n/2)-1
}
}
void HeapSort(int data[],int n){
for(int i=n;i>0;i--){
Swap(data,data+i-1);
AdjustHeap(data,0,i-1);
}
} 一道例题:以上代码是按照大根堆调整得出的,小根堆调整只需要修改比较参数即可;
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 |
| data | 7 | 3 | 5 | 9 | 1 | 12 |
拿到此类题目首先计算结点个数,找出最大的非叶子结点开始调整;最大非叶子结点下标为(n/2)-1;
6个元素非叶子结点为2号,其孩子结点只有左孩子且满足小根堆的定义无需调整;
在调整1号结点,其值为3,有一个比其小的右孩子(data[4]=1),交换得到一个小根堆满足要求;
最后调整0号结点,其值为7,有一个比其小的左孩子(data[1]=1),交换后其左子树部分不满足小根堆定义,
此时一号结点为7,有一个比其小的右孩子(data[4]=3),交换后满足要求;
最后得到的建堆序列为:
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 |
| data | 1 | 3 | 5 | 9 | 7 | 12 |
建堆图示:
时间复杂度:O(nlog2n); 稳定性:不稳定;
希尔排序(缩小增量排序):
定义:每一次取不同的增量,在每一组增量内部采用直接插入排序,每一次排序完成增量内部元素有序,在排序的最后一次
所取得增量必为1。(一般情况下理】第一次增量区间d选取为n/2(表长的一半),之后依次为上一次的一半)
}
void ShellSort(int data[],int n){
//默认增量为序列长度的1/2
for(int i=n/2;i>=1;i=i/2){
for(int j=i;j=i&&temp 归并排序:(分治法)
算法思想: 归并排序主要分为两步:分数列(divide),每次把数列一分为二,然后分到只有两个元素的小数列;合数列
(Merge),合并两个已经内部有序的子序列,直至所有数字有序。用递归可以实现。
时间复杂度:O(nlog2n); 稳定性:稳定;
基数排序(桶排序):(非重点)
基数排序,第一步根据数字的个位分配到每个桶里,在桶内部排序,然后将数字再输出(串起来);然后根据十位分桶,继续排
序,再串起来。直至所有位被比较完,所有数字已经有序。
时间复杂度:O(d(n+r)); 稳定性:稳定;
排序的每一次过程中是否可以确定一个待排元素的位置:
| 排序名称 | 位置是否确定 | 原因 |
| 冒泡排序 | 是 | 每一次排序最大(最小)的元素总位于相应的位置 |
| 直接插入排序 | 不一定 | 无序序列中仍可能有元素改变有序序列元素的位置 |
| 折半插入排序 | 不一定 | 无序序列中仍可能有元素改变有序序列元素的位置 |
| 希尔排序 | 不一定 | 元素在最后一次排序中达到稳定 |
| 快速排序 | 是 | 确定为基准的元素位于排序后的位置 |
| 堆排序 | 是 | 大(小)根堆根部元素与最后一个元素交换位置 |
| 简单选择排序 | 是 | 每一次选择的是序列中的最大(小)值,位置确定 |
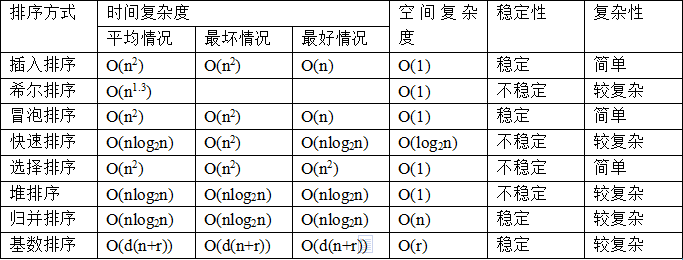
各个排序算法的时间/空间复杂度以及稳定性分析:
![]()
总结:对于时间复杂度小的,其排序大多情况下是不稳定的;