要点初见:反用OpenCV3中的卡尔曼滤波器(KalmanFilter)进行运动预测
卡尔曼滤波器是一种由卡尔曼(Kalman)提出的用于时变线性系统的递归滤波器。这个系统可用包含正交状态变量的微分方程模型来描述,这种滤波器是将过去的测量估计误差合并到新的测量误差中来估计将来的误差。OpenCV中自带Kalman滤波器,相关原理可以参考这位博主的博客,本文不做详述:
学习OpenCV2——卡尔曼滤波(KalmanFilter)详解
运动预测方面,起因是博主在通过视觉算法控制PID云台指向运动目标时遇到的延迟问题:从 摄像头捕获目标坐标 到 机械云台转到对应的角度 有一定的延迟,在这段时间内目标可能已运动到一个新的角度位置,因此需要在捕获坐标后即要对目标的位置进行提前预测。一般运动预测需要建立运动模型,但比较困难;博主被安利了Kalman滤波器后,参考PID控制原理,发现Kalman滤波器在某种情况下也可实现运动预测。
直接使用Kalman滤波器对实际坐标点进行处理是不能立即得到预测点的,从实际使用中可见处理的结果会先延迟于当前坐标点(摄像头识别到目标的那个时刻的坐标点),之后再回归、超前于当前点,但又会再次落后于当前点,再回归、超前,如此反复。典型的例子是OpenCV3.3的Sample中自带的一维Kalman滤波器——对旋转的角度进行Kalman预测:
#include "opencv2/video/tracking.hpp"
#include "opencv2/highgui.hpp"
#include
using namespace cv;
static inline Point calcPoint(Point2f center, double R, double angle)
{
return center + Point2f((float)cos(angle), (float)-sin(angle))*(float)R;
}
static void help()
{
printf( "\nExample of c calls to OpenCV's Kalman filter.\n"
" Tracking of rotating point.\n"
" Rotation speed is constant.\n"
" Both state and measurements vectors are 1D (a point angle),\n"
" Measurement is the real point angle + gaussian noise.\n"
" The real and the estimated points are connected with yellow line segment,\n"
" the real and the measured points are connected with red line segment.\n"
" (if Kalman filter works correctly,\n"
" the yellow segment should be shorter than the red one).\n"
"\n"
" Pressing any key (except ESC) will reset the tracking with a different speed.\n"
" Pressing ESC will stop the program.\n"
);
}
int main(int, char**)
{
help();
Mat img(500, 500, CV_8UC3);
KalmanFilter KF(2, 1, 0);
Mat state(2, 1, CV_32F); /* (phi, delta_phi) */
Mat processNoise(2, 1, CV_32F);
Mat measurement = Mat::zeros(1, 1, CV_32F);
char code = (char)-1;
for(;;)
{
randn( state, Scalar::all(0), Scalar::all(0.1) );
KF.transitionMatrix = (Mat_(2, 2) << 1, 1, 0, 1);
setIdentity(KF.measurementMatrix);
setIdentity(KF.processNoiseCov, Scalar::all(1e-5));
setIdentity(KF.measurementNoiseCov, Scalar::all(1e-1));
setIdentity(KF.errorCovPost, Scalar::all(1));
randn(KF.statePost, Scalar::all(0), Scalar::all(0.1));
for(;;)
{
Point2f center(img.cols*0.5f, img.rows*0.5f);
float R = img.cols/3.f;
double stateAngle = state.at(0);
Point statePt = calcPoint(center, R, stateAngle);
Mat prediction = KF.predict();
double predictAngle = prediction.at(0);
Point predictPt = calcPoint(center, R, predictAngle);
randn( measurement, Scalar::all(0), Scalar::all(KF.measurementNoiseCov.at(0)));
// generate measurement
measurement += KF.measurementMatrix*state;
double measAngle = measurement.at(0);
Point measPt = calcPoint(center, R, measAngle);
// plot points
#define drawCross( center, color, d ) \
line( img, Point( center.x - d, center.y - d ), \
Point( center.x + d, center.y + d ), color, 1, LINE_AA, 0); \
line( img, Point( center.x + d, center.y - d ), \
Point( center.x - d, center.y + d ), color, 1, LINE_AA, 0 )
img = Scalar::all(0);
drawCross( statePt, Scalar(255,255,255), 3 );
drawCross( measPt, Scalar(0,0,255), 3 );
drawCross( predictPt, Scalar(0,255,0), 3 );
line( img, statePt, measPt, Scalar(0,0,255), 3, LINE_AA, 0 );
line( img, statePt, predictPt, Scalar(0,255,255), 3, LINE_AA, 0 );
if(theRNG().uniform(0,4) != 0)
KF.correct(measurement);
randn( processNoise, Scalar(0), Scalar::all(sqrt(KF.processNoiseCov.at(0, 0))));
state = KF.transitionMatrix*state + processNoise;
imshow( "Kalman", img );
code = (char)waitKey(100);
if( code > 0 )
break;
}
if( code == 27 || code == 'q' || code == 'Q' )
break;
}
return 0;
}

其中黄色、红色线之间即为实际的坐标点,黄色线不相连的一端为预测点,红色线不相连的一端为观察点(实际点+噪声,因此有时超前,有时落后,加噪声目的在于显示Kalman滤波器对噪声的鲁棒性)。明显可见,预测点先落后于实际坐标点与测量点,从而使Kalman的预测变得激进,从而之后超前于实际坐标点,但一段时间后又落后,如此反复。
其实也可以理解,因为Kalman滤波器本身主要是用于对较杂乱目标的坐标进行滤波,以实现轨迹跟踪,因此有“迟钝性”,能将偏激的运动“折半”,从而将轨迹稳定。如果我们直接将其用在二维坐标的运动上,结果如下方这个C++类封装的Kalman滤波器所示:
该例简单的说,是用Kalman滤波器对一个横向匀速运动的点用Kalman滤波器进行“预测”,为方便观察Kalman滤波器的效果,输入数据中暂时不加入噪声(加入噪声则可使Kalman滤波器的预测效果更明显)。功能大多数在注释中描述:
#include
/*
"**" after "//" means the values are relative to Kalman regression speed.
*/
using namespace std;
using namespace cv;
namespace Kalman_example
{
class KalmanFilter
{
public:
KalmanFilter(int x, int y):
KF_(4, 2)
/*
KalmanFilter( int dynamParams, int measureParams, int controlParams = 0, int type = CV_32F )
"dynamParams = 4": 4*1 vector of state (x, y, delta x, delta y)
"measureParams = 2": 2*1 vector of measurement (x, y)
*/
{
measurement_ = Mat::zeros(2, 1, CV_32F);// (x, y)
KF_.transitionMatrix = (Mat_(4, 4) << 1, 0, 1, 0,//**Latter 1: Larger, faster regression
0, 1, 0, 1,//**Latter 1: Larger, faster regression
0, 0, 1, 0,
0, 0, 0, 1);
setIdentity(KF_.measurementMatrix, Scalar::all(1));
setIdentity(KF_.processNoiseCov, Scalar::all(1e-3));//**3: Larger, slower regression
setIdentity(KF_.measurementNoiseCov, Scalar::all(1e-1));//1: Larger, quicker regression
setIdentity(KF_.errorCovPost, Scalar::all(1));
KF_.statePost = (Mat_(4, 1) << x, y, 0, 0);//Ensure beginner is default value
}
Point2f run(float x, float y)
{
Mat prediction = KF_.predict();
Point2f predict_pt = Point2f(prediction.at(0),prediction.at(1));
measurement_.at(0, 0) = x;
measurement_.at(1, 0) = y;
KF_.correct(measurement_);
return predict_pt;
}
private:
Mat measurement_;
cv::KalmanFilter KF_;//Differ from Kalman_example::KalmanFilter
};
}
int main()
{
float size_x = 1280;//cols of side
float size_y = 480;//rows of side
float x = 20;//CV_32F: float
float y = 240;//CV_32F: float
int color = 0;//gradually varied color
Mat image(size_y, size_x, CV_8UC3);
Kalman_example::KalmanFilter kf(x, y);//Differ from cv::KalmanFilter
Point2f currentPoint(x,y);
Point2f kalmanPoint(x,y);
while(1)
{
//image = Scalar(0,0,0);//Clear points before
currentPoint = Point2f(x,y);
kalmanPoint = kf.run(x,y);
circle(image,kalmanPoint,3,Scalar(0,255,0 + color),2);//predicted point with green
circle(image,currentPoint,3,Scalar(255,0,0 + color),2);//current position with red
imshow("KalmanPoint", image);
cout << "Current: " << currentPoint << " Kalman: " << kalmanPoint << endl;
x+=105;
//y+=10;
color+=20;
waitKey(1000);
if(color>=255)
{
color = 255;
}
if((x>=size_x) || (y>=size_y) || (x<=0) || (y<=0))
{
imwrite("KalmanPoint.jpg", image);
break;
}
}
return 0;
}
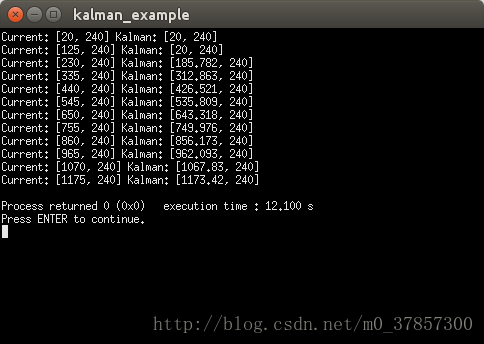
其实上例中的这个Kalman滤波器处理的仍暂时是一维数据,若将其中的y+=10从注释里释放出来,则是二维Kalman处理。其输出结果如下:
该例中的点从左到右运动,绿色为Kalman滤波器的预测点,蓝色为实际的匀速运动坐标点。随着时间的递增,点的颜色也渐变。可见,预测点先大幅度落后于蓝色的实际点,但逐渐追上并与蓝色的点重合。这在下方输出的数据中体现得更为明显:
从数据中可见,预测点的横坐标先大幅度落后于实际点的横坐标,但在若干帧后逐渐缩小了与目标的差距。若在系统中加上高斯噪声,预测点有可能在一定时间后超过目标点,实现运动预测。但这段时间也未免太长了!!在摄像头有限的视角内明显爆发性的运动更多,而在初始的这段时间内一直落后于当前点的“设定”对于运动爆发力较强的目标完全无用,即使后续的预测追上了实际点,目标也可能已经改变运动方向或移出视野,那还不如直接使用实际点呢。博主试过试图通过加速Kalman滤波器的回归速度来减少这段落后的时间,但这样却又大大削弱了预测的效果:从原理上说,回归速度越慢,预测的幅度越大。从减少落后时间着手似乎是个悖论。
所以应该如何将Kalman滤波器修改得更适应爆发性运动呢?
不如将Kalman滤波器的“落后”反过来用吧!
如上例中所示,Kalman滤波器将先大幅度落后于实际点:那我们可以考虑将实际点与Kalman预测点相减,将结果乘以一个系数,加在实际点的坐标上,从而实现“爆发性的运动”:我们将这个爆发性运动的点成为“反Kalman滤波器预测点”——当Kalman滤波器的预测点与实际点超过一定的距离时,该点将如脱缰的野马,出现在预测点的反方向较远的一个位置;而随着Kalman的结果逐渐回归,这个“反Kalman滤波器预测点”将逐渐靠近实际点(在这个过程中仍是一直超前于实际点);当Kalman的结果开始超前于实际点时,该点的作用相当于踩了一脚刹车(因为当前目标大概率已经停止运动);当Kalman滤波器的预测点与实际点小于一定的距离时,人为将预测点与实际点重合,避免抖动。
这个“反Kalman滤波器预测点”考虑到了云台PID的控制原理:PID在运动距离较大时,将先转一个较大的角度,再逐渐修正若干个较小的角度,从而达到目的点。而“反Kalman滤波器预测点”恰好先提供了一个较远的点,使云台快速转动,因PID的这个特点,云台又不至于立即转到那个较远的点上,从而避免了过度预测。考虑到从 视觉识别得到结果 到 机械云台转动到对应的位置 的时间延迟,“反Kalman滤波器预测点”的效果恰好能预测、追上这段时延。
**重要:反Kalman滤波器预测点只有摄像头中心跟着目标运动时,才能看出提前的效果。若摄像头视野并不随着目标点运动,该方法只会显示出一个不断累积的值,该值没有任何意义。
在摄像头中,三维目标一般是x、y轴线性运动的(除非车辆在转弯),用麦克纳姆轮的机器车辆更如是,因此在博主的测试中,“反Kalman滤波器预测点”在通过视觉算法控制PID云台指向运动目标方面的实时性较为良好,通过修改相关参数(回归速度、激进程度)能胜任对不同爆发性运动的预测。以下是对上例进行改动,实现“反Kalman滤波器预测点”(功能大多数在注释中描述):
#include
/*
"**" after "//" means the values are relative to Anti-Kalman regression speed and radical range.
*/
using namespace std;
using namespace cv;
namespace Kalman_example
{
class KalmanFilter
{
public:
KalmanFilter(int x, int y):
KF_(4, 2)
/*
KalmanFilter( int dynamParams, int measureParams, int controlParams = 0, int type = CV_32F )
"dynamParams = 4": 4*1 vector of state (x, y, delta x, delta y)
"measureParams = 2": 2*1 vector of measurement (x, y)
*/
{
measurement_ = Mat::zeros(2, 1, CV_32F);// (x, y)
KF_.transitionMatrix = (Mat_(4, 4) << 1, 0, 1, 0,//**Latter 1: Larger, faster regression
0, 1, 0, 1,//**Latter 1: Larger, faster regression
0, 0, 1, 0,
0, 0, 0, 1);
setIdentity(KF_.measurementMatrix, Scalar::all(1));
setIdentity(KF_.processNoiseCov, Scalar::all(1e-10));//**10: Larger, slower regression
setIdentity(KF_.measurementNoiseCov, Scalar::all(1e-1));//1: Larger, quicker regression
setIdentity(KF_.errorCovPost, Scalar::all(1));
KF_.statePost = (Mat_(4, 1) << x, y, 0, 0);//Ensure beginner is default value
}
Point2f run(float x, float y)
{
Mat prediction = KF_.predict();
Point2f predict_pt = Point2f(prediction.at(0),prediction.at(1));
measurement_.at(0, 0) = x;
measurement_.at(1, 0) = y;
KF_.correct(measurement_);
return predict_pt;
}
private:
Mat measurement_;
cv::KalmanFilter KF_;//Differ from Kalman_example::KalmanFilter
};
}
int main()
{
float size_x = 1280;//cols of side
float size_y = 480;//rows of side
float x = 20;//CV_32F: float
float y = 240;//CV_32F: float
int color = 0;//gradually varied color
float anti_range = 0.5;//**Larger, anti-kalman more radical
Mat image(size_y, size_x, CV_8UC3);
Kalman_example::KalmanFilter kf(x, y);//Differ from cv::KalmanFilter
Point2f currentPoint(x,y);
Point2f kalmanPoint(x,y);
Point2f anti_kalmanPoint(x,y);
while(1)
{
//image = Scalar(0,0,0);//Clear points before
currentPoint = Point2f(x,y);
kalmanPoint = kf.run(x,y);
if((currentPoint.x + anti_range*(currentPoint.x - kalmanPoint.x))<=size_x
|| (currentPoint.x + anti_range*(currentPoint.x - kalmanPoint.x))>=0)//Prevent Anti-kal out of Mat
{
if(abs(currentPoint.x - kalmanPoint.x) > 3)//When points are closed, no Anti-kalman to reduce shaking
anti_kalmanPoint.x = currentPoint.x + anti_range*(currentPoint.x - kalmanPoint.x);
else
anti_kalmanPoint.x = currentPoint.x;
}
else
{
anti_kalmanPoint.x = currentPoint.x;
}
//y is the same.
circle(image,anti_kalmanPoint,3,Scalar(0,255,0 + color),2);//predicted point with green
circle(image,currentPoint,3,Scalar(255,0,0 + color),2);//current position with red
imshow("Anti-KalmanPoint", image);
cout << "Current: " << currentPoint << " Kalman: " << kalmanPoint << " Anti-Kalman: " << anti_kalmanPoint << endl;
x+=105;
//y+=10;
color+=20;
waitKey(1000);
/*
if(TargetLost_times > 60)//Initialize Kalman Filter when losing target in a long time
{
KalmanFilter();
}
*/
if(color>=255)
{
color = 255;
}
if((x>=size_x) || (y>=size_y) || (x<=0) || (y<=0))
{
imwrite("Anti-KalmanPoint.jpg", image);
break;
}
}
return 0;
}
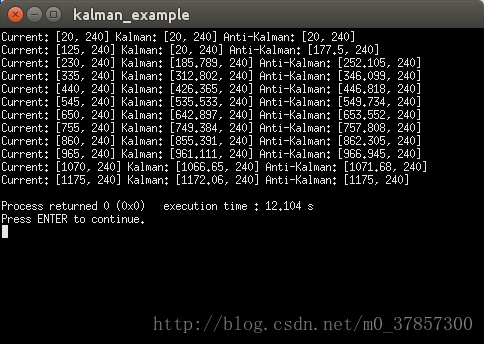
同上一个例子,若将该例中的y+=10从注释里释放出来,则是二维Kalman处理。其输出结果如下:

该例中的点从左到右运动,绿色为反用Kalman滤波器得到的预测点,蓝色为实际的匀速运动坐标点。随着时间的递增,点的颜色也渐变。可见,预测点先大幅度超前于蓝色的实际点,但逐渐缩短于蓝色点的距离,最终重合。这在下方输出的数据中体现得更为明显:
很明显,这种反用Kalman滤波器的方法可以有效地进行运动预测,对运动爆发性较好的目标效果明显,非常适合需通过PID控制机械结构运动的视觉算法。可能存在的问题是,反用Kalman滤波器对突然改变运动方向的目标容易过度预测。
上例中大部分细节都在注释中进行了解释,但博主特别想强调其中
/*
if(TargetLost_times > 60)//Initialize Kalman Filter when losing target in a long time
{
KalmanFilter();
}
*/博主对卡尔曼滤波器的理解还较为初步,这篇博文大多数是基于先前项目的结果进行的总结。欢迎交流讨论!