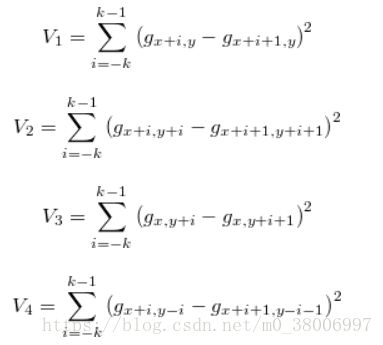数字摄影测量之——Matlab实现Moravec算子的边缘点提取
一、Moravec算子简介
Moravec(1977)是第一个提出兴趣点这一概念的人。所谓兴趣点也即图像的点特征,是影像曲面上具有确定的、明显表现(或特殊性质)的像点,如灰度值变化明显的点或亮度特别明显的小区域(Blob)、边缘的焦点及一些区域或轮廓的交点及一些区域或轮廓的角点等。
Moravec算子在四个方向上计算非归一化的影像局部灰度差方差,将最小值作为兴趣值测度。因此,该算子检测的特征点是那些影响强度值在每个方向上变化剧烈的点。
二、算法步骤:
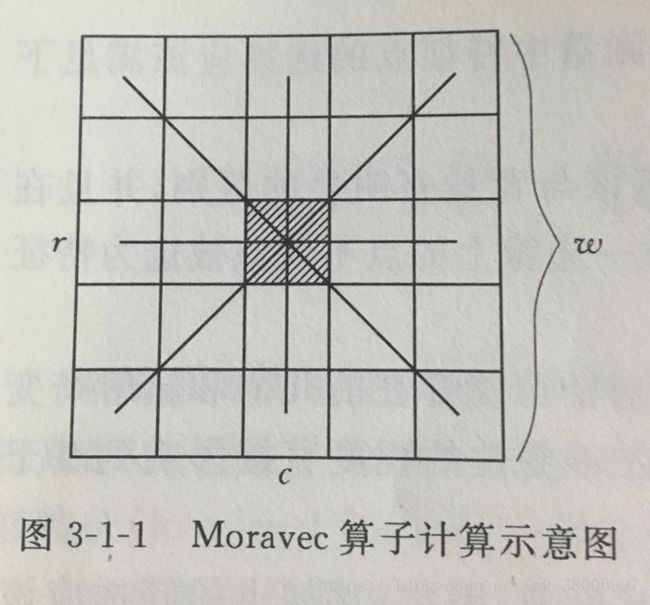
1、首先计算各像素的兴趣值。在以像素(r,c)为中心的w×w的影像窗口内,计算四个方向相邻像素灰度差的平方和。然后取四个方向上值最小者作为该像素的兴趣值。
2、给定阈值,将兴趣值大于该阈值的店(即兴趣值计算窗口的中心点)作为候选点。阈值的选择以候选点中包括所需要的特征点而又不含过多的非特征点为原则。
3、选候选点中兴趣值极大的点作为特征点。在一定大小的窗口内(可不同于兴趣值计算的窗口大小),将候选点中兴趣值不是最大者去掉,仅留下兴趣值最大者,该像素即为特征点,该过程成为抑制局部非最大。
以上即为Moravec算子的基本实现算法,下面附上Matlab实现的代码。
close all;
clear all;
clc;
img=(imread('lena512color.tif'));
img = double(rgb2gray(img));
[X,Y]=size(img);
img2 = imread ('lena512color.tif');
img2 = rgb2gray(img2);
figure;
subplot (1,2,1);
imshow(img2);
title('原图像');
imgn=zeros(X,Y);
n=2;%控制窗口大小。窗口大小为 2*n+1
for x=1+n:X-n
for y=1+n:Y-n
window=img(x-n:x+n,y-n:y+n);%窗口为5*5
V=zeros(1,4);
for i=2:2*n+1 %垂直,水平,对角,反对角四个方向领域灰度差的平方和
V(1)=V(1)+(window(i,n+1)-window(i-1,n+1))^2;%垂直
V(2)=V(2)+(window(n+1,i)-window(n+1,i-1))^2;%水平
V(3)=V(3)+(window(i,i)-window(i-1,i-1))^2;%正对角线
V(4)=V(4)+(window(i,(2*n+1)-(i-1))-window(i-1,(2*n+1)-(i-2)))^2;%反对角线
end
IV=min(V); %四个方向中选最小值
imgn(x,y)=IV;
end
end
% count1 = X*Y;
% T=0.01*max(max(imgn)); %取最大值的0.01倍
T=2000; %手动经验阈值 % 效果最好
% % % sortarray= sort(imgn(:),'descend');%降序排序
% % % T = mean(sortarray(1:(count1*0.2)));%求降序排序的前百分之20的均值
% T = mean(imgn(:)); %均值阈值
ind=find(imgn
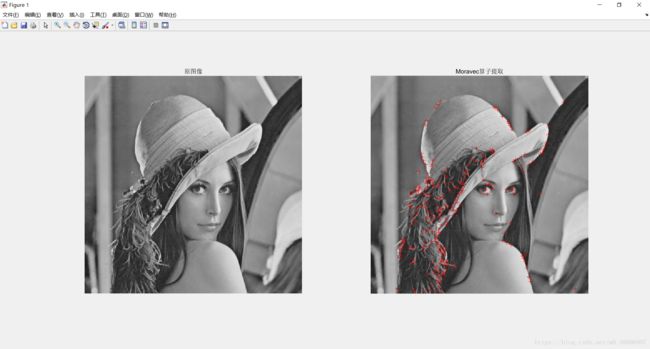
程序运行结果如下:
代码为原创,感谢阅读,欢迎交流和指正。