机器学习入门(2)----程序员薪资建模(未完)
1.线性回归的简单模拟
#数据分析库
import pandas as pd
#科学计算库
import numpy as np
from pandas import Series,DataFrame
import matplotlib.pyplot as plt
import seaborn as sns
import random
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
data_all = pd.read_excel("alldata.xlsx")
#这里如果使用read—_csv会产生报错,因为d.read.csv默认分隔符是“,”,倘若文档中存在该字符,则会自动分割
#解决办法:改变默认的分隔符
'''
在pd.read_csv中加入参数sep设置为None或者别的字符如\t
如:
data = pd.read_csv(“E:/test/datas/new/11-new.txt”,encoding=“utf-8”,header=None,sep = None)
'''
print(data_all.head(5))#查看前五行
print(data_all.info())#查看 基本信息
#可以看到,数据共1305条,数据类型,以及数据并无缺失,这里省略数据空值处理的过程
'''公司代号与其他关系不大,暂且忽略'''
print('数据集划分')
from sklearn.utils import shuffle
df = shuffle(data_all,random_state = 25)#使用sklearn打乱数据集
data_train= df[0:900]
data_test= df[901:1305]
from sklearn.linear_model import LinearRegression
#训练集交叉验证,得到平均值
#from sklearn.cross_validation import KFold
from sklearn.model_selection import KFold
#选取简单的可用输入特征
#初始化现行回归算法
alg = LinearRegression()
#样本平均分成3份,3折交叉验证
#kf = KFold(data_train.shape[0],n_folds=3,random_state=1)
kf = KFold(n_splits=3,shuffle=False,random_state=1)
#这里 为了分类方便,将python工程师设定为0,数据分析师设定为1,前端工程师设定为2
#工作年限,公司规模等也以均值代替,并且需要进行数据归一化处理
from sklearn import preprocessing
X = np.array(data_all['公司规模']).reshape(-1, 1)
y = np.array(data_all['最小值']).reshape(-1, 1)
from sklearn import linear_model
model = linear_model.LinearRegression()
model.fit(X, y)
display(model.intercept_) #截距
display(model.coef_) #线性模型的系数
a = model.predict([[2000]])
# a[0][0]
print("预测",int(model.predict([[2000]])[0][0]))
a = int(model.predict([[2000]])[0][0])
#准确率比较低,说明拟合效果并不好
#加入特征公司规模后拟合准确率提升
list = []
for i in data_all['最小值']:
if abs(int(a)- i)<=2000:
list.append(i)
print('模型预测准确率为:',len(list)/sum(data_all['公司规模']==2000))
输出
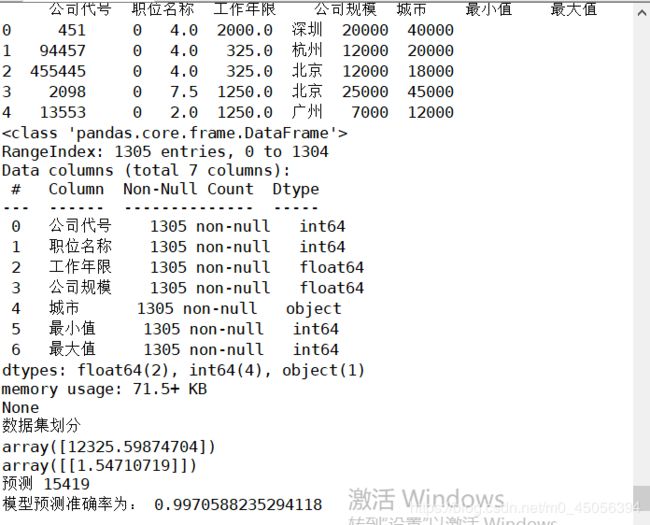
此处拟合了公司规模和工资最小值,以公司规模2000人作为预测值,预测结果为15419,与预测结果误差在2000以内的准确率为99.7%。
可以看到简单的线性回归拟合公司规模及工资最小值的准确率较高,此处的数据因为是范围直接取平均值,所以多为离散而不连续的点。因此误差范围定于2000,实际数据应该更加连续,拟合效果会更好。
如图

plt.title(u'散点图')
plt.scatter(data_all['公司规模'], data_all['最小值'],color='b',marker='*')
plt.scatter(data_all['公司规模'], data_all['最大值'],color='r')
plt.legend(['最小值','最大值'])
plt.show()
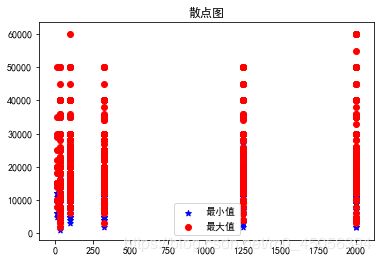
接下来我们来尝试一下多元线性回归,计算出每个因素的权重,因为公司代号和职位影响较小暂且去掉,保留公司规模和工作年限对工资最小值进行拟合
predictors = ["最小值","最大值"]
#初始化逻辑回归算法
#sns.pairplot(data_all, x_vars=['工作年限','公司规模','城市','最小值'], y_vars='最大值',kind="reg", size=5, aspect=0.7)
#plt.show()
#数据归一化
from sklearn.model_selection import train_test_split #这里是引用了交叉验证
from sklearn.linear_model import LinearRegression #线性回归
def build_lr():
X = data_all.loc[:, ('工作年限','公司规模')]
y = data_all.loc[:, '最小值']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=532)#选择20%为测试集
print('训练集测试及参数:')
print('X_train.shape={}\n y_train.shape ={}\n X_test.shape={}\n, y_test.shape={}'.format(X_train.shape,
y_train.shape,
X_test.shape,
y_test.shape))
print(X_train,X_test,y_train,y_test)
linreg = LinearRegression()
#训练
model = linreg.fit(X_train, y_train)
print('模型参数:')
print(model)
# 训练后模型截距
print('模型截距:')
print (linreg.intercept_)
# 训练后模型权重(特征个数无变化)
print('参数权重:')
print (linreg.coef_)
y_pred = linreg.predict(X_test)
sum_mean = 0
for i in range(len(y_pred)):
sum_mean += (y_pred[i] - y_test.values[i]) ** 2
sum_erro = np.sqrt(sum_mean /len(y_pred)) # 测试级的数量
# calculate RMSE
print ("RMSE by hand:", sum_erro)
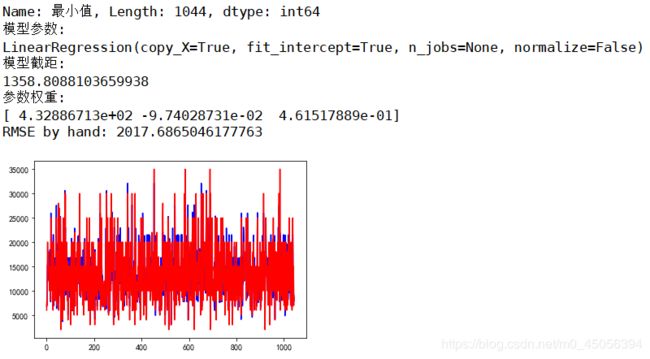
# 做ROC曲线
plt.figure()
plt.plot(range(len(y_pred)), y_pred, 'b', label="predict")
plt.plot(range(len(y_pred)), y_test, 'r', label="test")
plt.show()
build_lr()
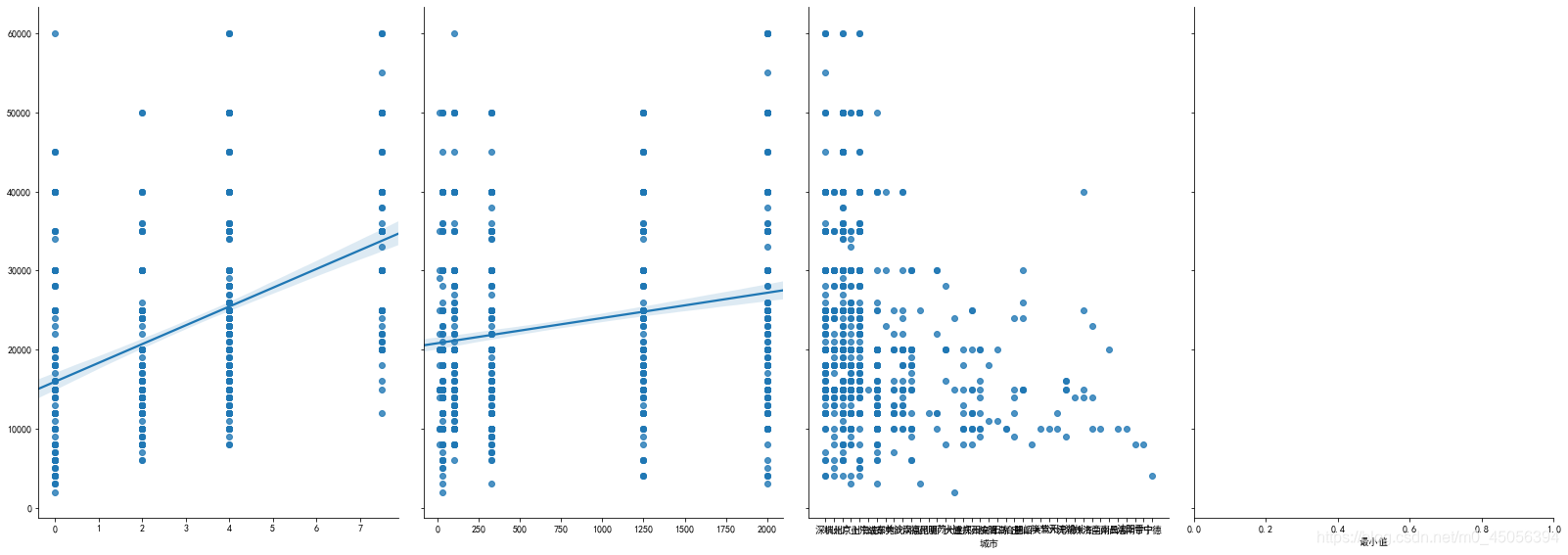
这个图纯粹就是看着开心,因为数据本身非常分散且不连续,象征性看一下,但是还是能看出来不同水平城市对IT工作人员的需求量还是有普遍差别的
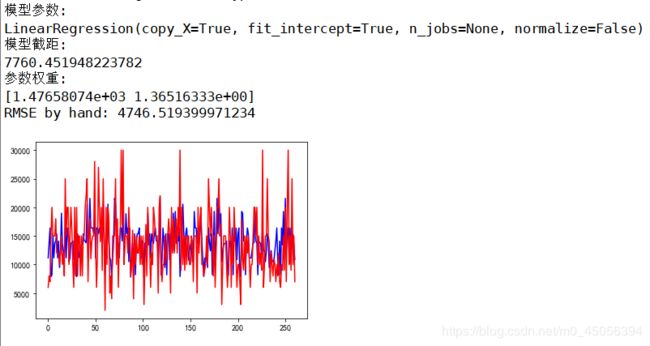
可以看出工作年限和公司规模对薪资最小值影响的权重还是非常相近的,但是模型拟合效果并不好,因为数据本身和没有进行归一化等等 原因。蓝色代表测试数据集,红色代表训练数据集,可以看出效果还是非常勉强
这时候我们加入一个特征 最大值,想也知道其实应该是会大幅度提升预测准确率的
RMSE为均方根误差。