算法与数据结构-算法篇-快速排序

快速排序

Java里的Arrays有一个sort()方法，具体的排序细节就是使用快速排序进行的实现，它是一个不稳定的，追求排序速度的排序算法 ，时间复杂度O(N* logN)
它与归并的思路有相近之处，都是先保证局部有序，再保证整体有序
在引入快速排序前，需要先去引导出两个问题

一、如何在一个无序数组里指定一个数K，保证左侧所有数都小于等于K,右侧数都大于K

例1，数组[2,1,3,4,5,1,3],k=3,返回 [2,1,1,3,3,4,5]即可
例2，数组[2,1,4,2,4,5,3,6],k=6.返回原数组即可

思路

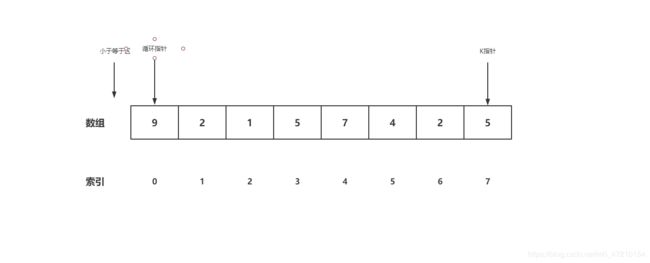
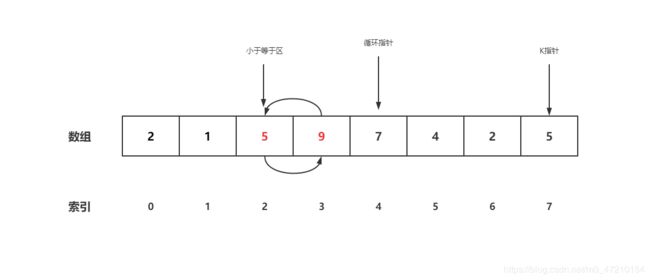
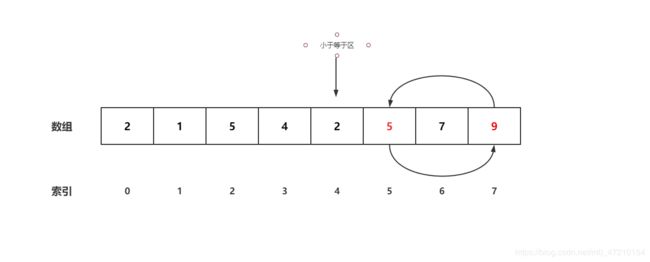
1. 将数组最右侧当成K，同时设计一个小于等于区，初始指针指向索引-1
2. 从0到length-2范围进行循环，循环时会遇到两种情况
3. 一、当前数小于等于K，将数字与小于等于指针前面一位的数进行交换，同时将指针向前移动
4. 二、当前数大于K，直接跳过
5. 走完一次循环后，小于等于区里的数都是小于等于K的，不在小于等于区里的数都是大于K的，此时，将小于等于区右侧第一个数和length-1位置交换，即可完成

示例

• 起始状态如图，将数组最后一个值当做K，同时设置一个小于等于区的指针
  
• 然后对比，发现9是大于5的，不做处理，循环的指针指向1号位置，结果如下

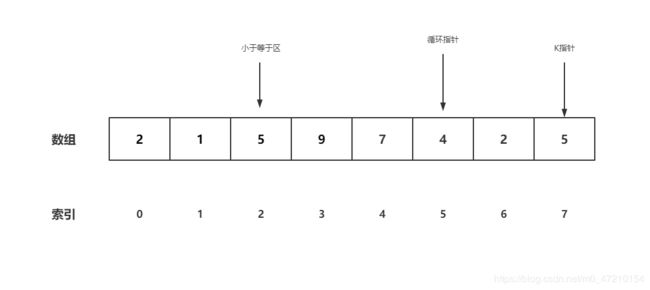
• 接下来再比较1号位与7号位，发现1号位小，开始进行交换，交换的对象是当前的循环指针与小于等于区右侧第一位，即交换0号位与1号位，小于等于指针右移，结果如下

• 比较2号位与7号位，发现2号位小，再交换，同时偏移小于等于指针，结果如下

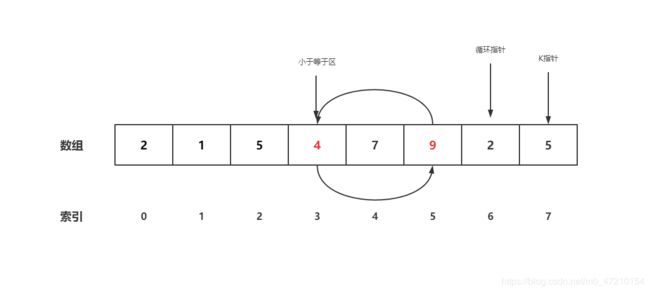
• 轮到3号位与7号位比较，发现相等，继续交换，同时偏移小于等于指针，结果如下

• 接着来，7大于5，不处理，结果如下
  
• 再比较5号位与7号位，4小于5，交换3号位与5号位，结果如下

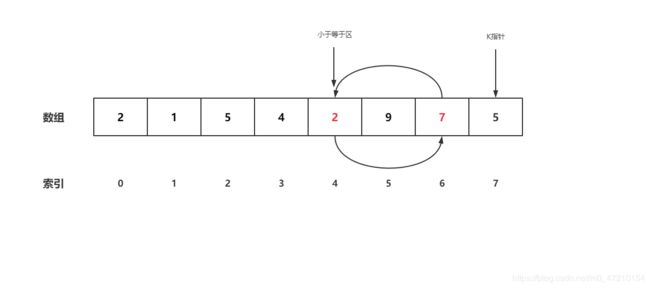
• 循环到倒数第二位，循环结束 ，2 小于5，交换 4与6号位置

• 到这里循环就已经走完，小于等于区里的五个数都是小于等于5的，此时只需要将小于等于区右侧的数与7号位进行交换，即可完成
  

demo

	public static void main (String[] args) {
        int[] arr = new int[]{1, 4, 76, 2, 3, 673, 5, 6, 73, 7, 9, 9, 8};
        new PartitionSort().partition(arr, 0, arr.length - 1);
        for (int i : arr) {
            System.out.printf(i + ",");
        }
    }

    public int partition (int[] arr, int left, int right) {
        if (left > right) {
            return -1;
        }
        if (left == right) {
            return left;
        }
        // 左边界
        int leftIndex = left - 1;
        //对数
        int num = arr[right];
        for (int i = left; i < right; i++) {
            //只要当前数小于等于对数，与小于区相邻的数交换
            if (arr[i] <= num) {
                //++left即小于区的相邻数
                swap(arr, ++leftIndex, i);
            }
        }
        swap(arr, ++leftIndex, right);
        return leftIndex;
    }

二、荷兰国旗问题

即如何在上一题的基础上，将数组分为三块，小于区，等于区，大于区

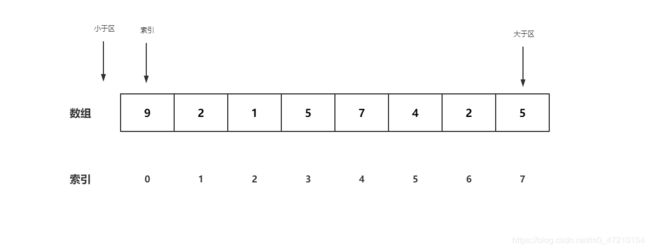
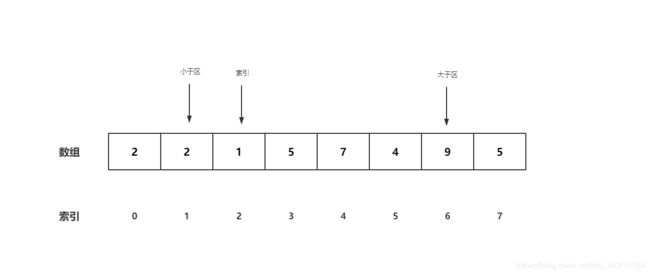
示例

• 还是和刚才一样，从0循环到length-2位置，不同的是同时设置了一个大于区
  

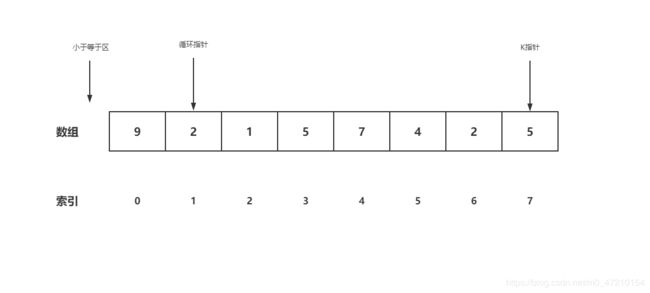
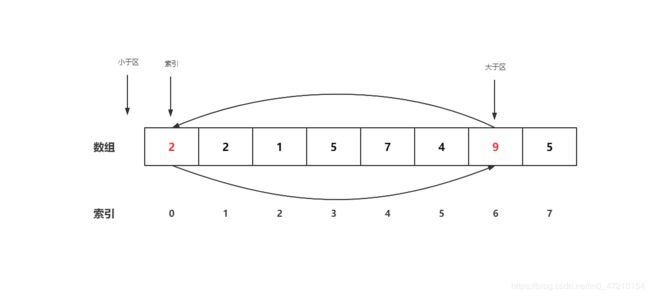
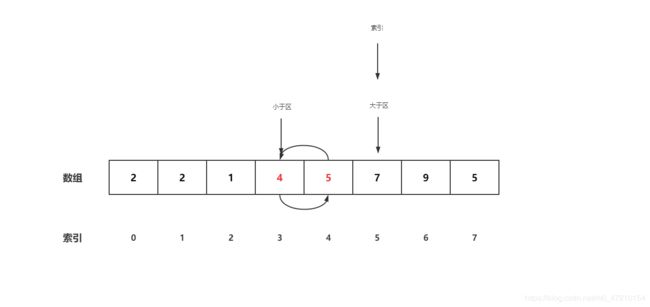
• 比较0号位与7号位，9大于5，向大于区左侧进行交换，即交换0号位与6号位，大于区左移。

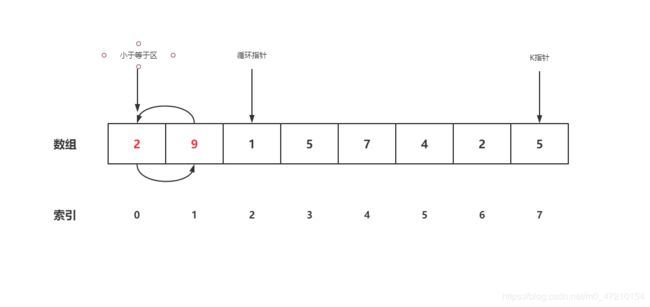
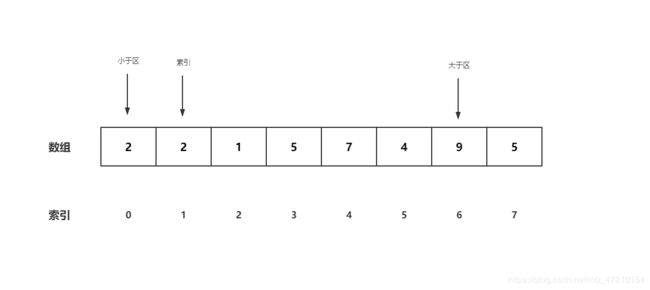
• 交换完有个细节，就是索引不加一，保持原位不动

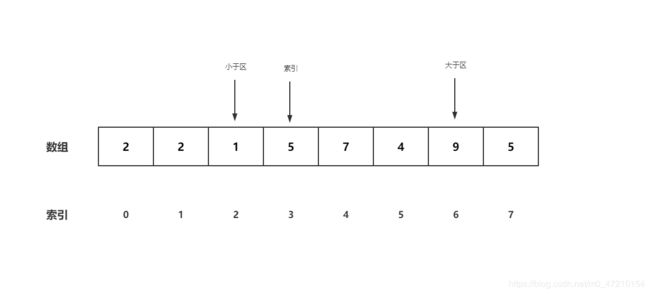
• 因为索引没有动，继续比较0号位，2小于5，OK，不需要处理，索引右移，小于区索引右移

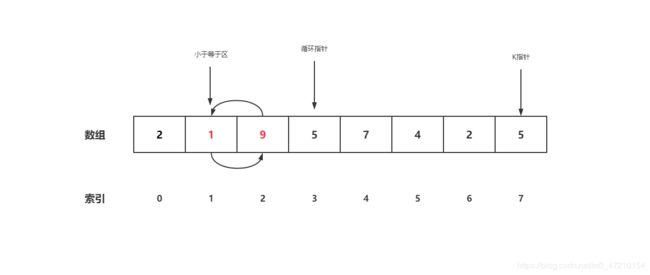
• 看下1号位，还是小于5，继续向前移动小于区索引和循环索引

• 再看2号位，1小于5，继续

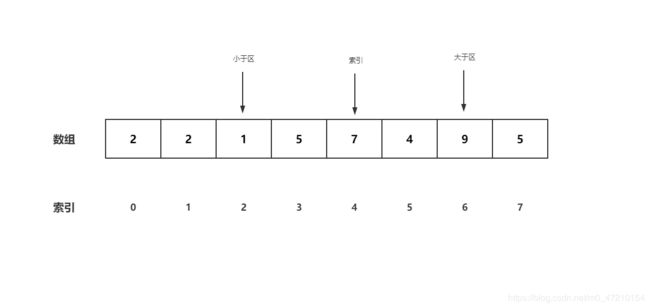
• OK，到了3号位，发现与5是等于关系 ，小于区不动，索引右移

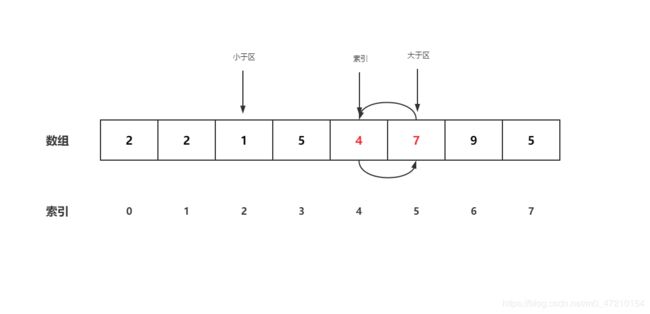
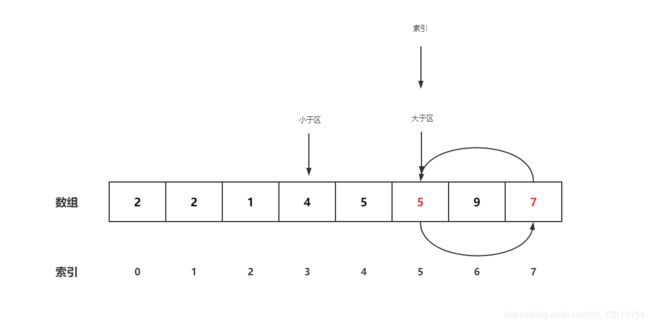
• 比较4号位，发现7大于5，OK，与大于区左侧交换，索引保持不动

• 因为索引没有动，再检查4号位置，发现小于5，和小于区右侧交换，即交换3号位和4号位，小于区右移，索引右移

• 此时发现索引和大于区相撞，说明排序已经完成，只需将大于区的第一个数和7号位置交换一下，完成

demo

	public int[] sort (int[] arr, int left, int right) {
        if (arr == null || right - left < 2) {
            return new int[]{-1, -1};
        }
        int num = arr[right];
        int position = left;
        int leftIndex = left - 1;
        int rightIndex = right;
        while (position <= rightIndex) {
            if (arr[position] < num) {
                swap(arr, position++, ++leftIndex);
            } else if (arr[position] > num) {
                swap(arr, position, --rightIndex);
            } else {
                position++;
            }
        }
        swap(arr, arr.length - 1, rightIndex);
        return new int[]{leftIndex, rightIndex};
    }

三、快速排序

从荷兰国旗问题中可以看出，给定一个数组，我可以在O(N)复杂度内，让他在某一小块上有序，即等于区的起止点，因此结合归并的思想，只要让每一小块排序都能确定出一部分以后不再需要排序的序列，合并后就是一个完整的排好序的集合

demo

public void quickSort (int[] arr, int left, int right) {
        if (left >= right) {
            return;
        }
        int[] partition = partition(arr, left, right);
        quickSort(arr, left, partition[0] - 1);
        quickSort(arr, partition[1] + 1, right);
    }

    private int[] partition (int[] arr, int left, int right) {
        if (right > left + 1) {
            int randomIndex = RANDOM.nextInt(right - left) + left;
            swap(arr, randomIndex, right);
        }
        int num = arr[right];
        int position = left;
        int leftIndex = left - 1;
        int rightIndex = right;
        while (position < rightIndex) {
            if (arr[position] < num) {
                swap(arr, position++, ++leftIndex);
            } else if (arr[position] > num) {
                swap(arr, position, --rightIndex);
            } else {
                position++;
            }
        }
        swap(arr, right, rightIndex);
        return new int[]{leftIndex + 1, rightIndex - 1};
    }