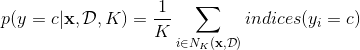MLAPP————第一章 简介
个人说明:
本人是机器学习方向的小白一个,虽然多次暗下决心想要认真看完例如PRML,MLAPP这两本书,却都坚持不下去,往往都是看完前几章就顿感力不从心,每次遇到问题解决不了就会搁置。至今在机器学习方面都是零零散散的学,西瓜书,李航的统计学习方法,也都并没有看完。所以主要想通过此博客来勉励促进自己,希望自己能够一步一个脚印坚持走下去,不想半途而废。当然如果该博客能够给他人带来哪怕一丝丝的帮助,那么也算是意外收获。
文中必然存在很多错误的地方,毕竟博主水平比较次,所以希望如有大牛发现,能给出点评。博主在看书时可能会遇到很多的问题,也会在上面呈现,对于这些问题,如若有人能给出指点,将会不胜感谢。此外如有同时看此书志同道合之人,欢迎交流。
最后希望自己能够在机器学习这条路上坚持的走下去,不要因为一时的挫折而气馁!
第一章 介绍
1.1 什么是机器学习
我们当前处于一个大数据的背景下(big data),机器学习是能够自动处理大量数据的方法。我们定义机器学习为从数据中自动检测模式的一系列方法,利用学习到的模式对新的数据进行预测。Murphy的这本书是从概率论的角度对机器学习进行深入的分析。
1.11 机器学习的分类
机器学习总共分为三类:监督学习(supervised learning),无监督学习(unsupervised learning)和强化学习(reinforcement learning),该书主要介绍监督学习和无监督学习。
监督学习主要是从训练数据![]() 中学习输入
中学习输入![]() 到输出y的映射关系,也称之为预测(predictive)。
到输出y的映射关系,也称之为预测(predictive)。![]() 我们一般称之为属性。当输出y是连续量是,此时问题称之为回归(regression),当输出y是离散量时,此时问题称之为分类(classification)。当我们的标记空间
我们一般称之为属性。当输出y是连续量是,此时问题称之为回归(regression),当输出y是离散量时,此时问题称之为分类(classification)。当我们的标记空间![]() 是有一些自然的顺序的,比如成绩A-F,此时归为传统的分类问题就不合适,因为没有利用A>B>C>D>E>F的特性,该类问题称为有序回归(ordinal regression)或有序分类(ordinal classification),这是一个介于回归和分类中间的一个问题。
是有一些自然的顺序的,比如成绩A-F,此时归为传统的分类问题就不合适,因为没有利用A>B>C>D>E>F的特性,该类问题称为有序回归(ordinal regression)或有序分类(ordinal classification),这是一个介于回归和分类中间的一个问题。
无监督学习主要是从训练数据![]() 中发现一些有趣的模式。有时也叫做知识发现。在这里要注意的是,无监督学习的数据是没有标签的。比较常见典型的无监督学习问题是聚类。即给你一些离散的点,然后通过学习对这些点进行分类。
中发现一些有趣的模式。有时也叫做知识发现。在这里要注意的是,无监督学习的数据是没有标签的。比较常见典型的无监督学习问题是聚类。即给你一些离散的点,然后通过学习对这些点进行分类。
第三种学习则是强化学习,该学习方法是对你的行为进行奖赏或者惩罚,通过自我学习,争取获得更多的奖赏而不是惩罚。
1.2 监督学习的一些例子
下面会给出监督学习的一些常见的例子
1.2.1 分类
在分类的问题中,对于输入![]() ,输出
,输出![]() ,当C = 2,我们一般称为二元分类,C > 2那么就称为多元分类。当然还有多输出的模型。比如对于人来说,高矮,胖瘦,就会有两个输出。在该书中,不加特殊说明就认为是单输出的模型。
,当C = 2,我们一般称为二元分类,C > 2那么就称为多元分类。当然还有多输出的模型。比如对于人来说,高矮,胖瘦,就会有两个输出。在该书中,不加特殊说明就认为是单输出的模型。
1.2.1.1 例子
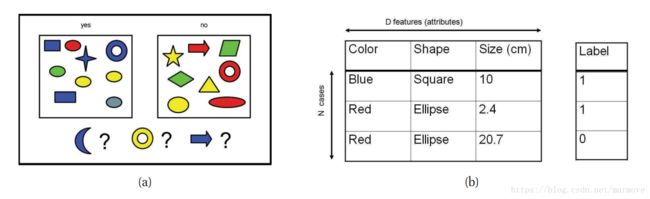
如上图(a),我们有一堆训练数据分成两类,左边是1即yes,右边的是0即no。这些数据有三个特征,分别是颜色,形状还有尺寸,如图(b)。那么根据以上的训练数据,如果给出下面的下个测试样例,蓝色的新月,黄色的圆环,蓝色的箭头,它们应该被分到哪一类。那么需要从训练数据中寻找一些模式,这个东西看着有点像公务员考试233。可以看到蓝色的全部被划分到了yes,那么我们有理由将蓝色的新月划分到yes。对于蓝色的箭头,但是我们又发现箭头都在no,那么很难抉择。黄色的圆环,也是很难选。当然这些都是给了一些直观上在做分类的感觉。
1.2.1.2 为什么需要进行概率预测
很好理解的一点就是,很多时候,没有办法进行直接对结果进行判决,例如上面黄色的圆环,很难说它属于哪一类,但是通过概率我们可以得到它属于每一类的概率![]() ,如果有C类的话,这是一个长度为C的向量。这个式子表示在训练数据为
,如果有C类的话,这是一个长度为C的向量。这个式子表示在训练数据为![]() ,输入特征为
,输入特征为![]() 的情况下,y的概率分布。对于分类问题,就是y=1,y=2...的概率。对于上面的问题,C等于2,我们只要选择y=0和y=1中概率大的那个作为最后的预测结果。
的情况下,y的概率分布。对于分类问题,就是y=1,y=2...的概率。对于上面的问题,C等于2,我们只要选择y=0和y=1中概率大的那个作为最后的预测结果。
所以对于给定的概率输出,选择概率最大的标签作为最终的估计标签:
![]() ,这就是最大后验概率估计(MAP,maximum a posteriori)。
,这就是最大后验概率估计(MAP,maximum a posteriori)。
1.2.1.3 现实当中的一些例子
接下来分类的一些显示生活当中的例子
文件的分类和电子垃圾邮件的过滤
很多时候我们需要对文件进行分类,尤其比如说垃圾邮件的分类,用过邮箱的都知道,你会有个垃圾邮箱的一个选项,有些邮件发送过来的时候就会分到这个类别里面去。那么这其实就是一个二分类的问题。对于一个邮件,系统要能够自动的判断这个邮件是否是垃圾邮件。对于这样一个问题,我们的特征是什么,即输入是什么,就是单词,所有的邮件都是通过一个词库表示的。假设该词库有100个单词,那么这封邮件就可以由一个100维的向量![]() 表示,如果第i个单词在该封邮件出现,那么
表示,如果第i个单词在该封邮件出现,那么![]() ,否则为0。假设我们的训练集有1000封邮件,那么输入的特征就可以用一个1000*100的矩阵构成。如下图所示
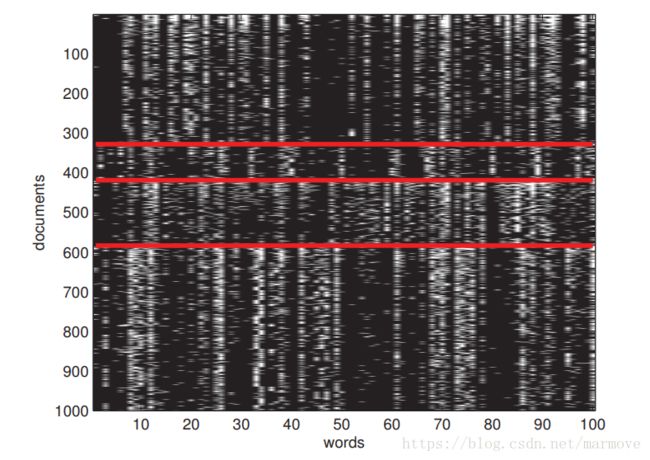
,否则为0。假设我们的训练集有1000封邮件,那么输入的特征就可以用一个1000*100的矩阵构成。如下图所示
红线将数据分成四类,不同的类别之间有着明显的差异,相同类别之间有很强的相似性。为什么我们能够通过这样的表达方式去进行垃圾邮件分类,很大是因为在很多的垃圾邮件中,都会很大概率上包含比如打折,便宜等一些词,所以仅通过单词就能较好的进行分类。
花瓣的分类
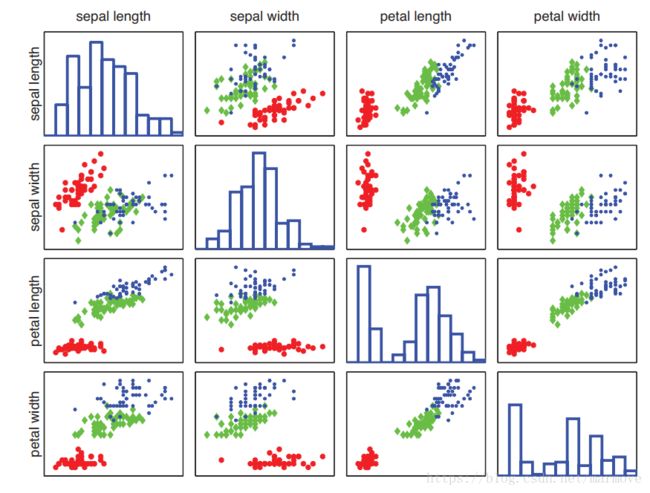
这一块主要给出了花的一些特征,花萼和花瓣的长度和宽度四个特征,去分辨一个花是setosa, versicolor 和 virginica 这三种花中的哪一个。这里提出了一个机器学习的难点,就是特征提取,现在有一些是通过人工提取,书中说了后面会提到如何通过一些算法提取。
根据这张图,我们发现只通过花瓣的长度和宽度,其实是能够相对较好的把这三种花给分辨出来,尤其是红色花,明显就是花瓣很小(长宽都小)就是该种花。所以很多时候,拿到数据,如果能够画图的话(维度较低),那么可以先通过把数据画出来,直观感受一下,再去思考去选用什么样的机器学习算法。
图像分类和手写识别
图像分类是现在很热门的方向,之前有过很多识别图片中是否有猫有狗,识别是否有汽车,有交通标志等。最典型的一个例子就是很多机器学习书中都会常用到的手写识别。这个技术现在基本上已经相当成熟了。问题就是识别手写的数字0-9。该问题中,输入就是一个28*28的灰度图片,每一个像素点的取值是0:255。当前比较流行的应该是通过深度学习的方法去做。
人脸的检测和识别
人脸识别是一个现在也经常会碰到的一个问题,人脸识别一般分为两个步骤,一个是人脸 的检测和定位,说白了就是把你的脸给抠出来,否则在很多背景的影响下是很难去做的。在抠出了脸之后再去识别这个脸到底是谁的。
1.2.2 回归
回归问题就是对于给定的训练数据,去找一个函数f(![]() ),输入一个
),输入一个![]() ,输出一个y。
,输出一个y。
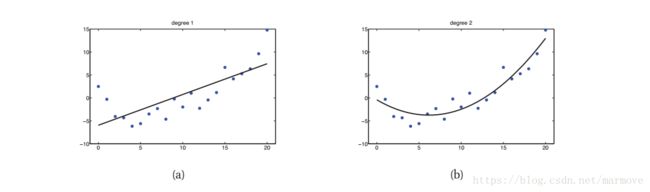
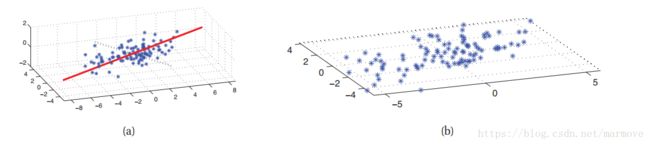
比如给如上的数据点,左边是用了一个一次函数去拟合,效果比较差,当然这也能预测,比如我给出一个x=30,这在原来的数据上是没有的,根据这个模型,y可能是13左右。右边是用了一个二次的函数去拟合,效果明显就好了很多。当然选什么样的函数去拟合,肯定是有根据的,该书后面会给出一些阐述。回归问题的应用其实还是比较多的,比如房价的预测,股市的预测,温度的预测等等一系列的问题都可以看成是回归的问题。
1.3 无监督学习
现在我们来考虑无监督的学习,无监督学习主要就是是一种直接从数据本身学习的一个过程,给出的是我们输入特征的概率分布,在监督学习中我们是学习![]() 而在无监督学习中,我们想要获得的是
而在无监督学习中,我们想要获得的是![]() ,是数据本身的概率分布。一般来说,无监督学习的概率密度函数是多变量的,而监督学习则是单变量的。无监督学习跟我们人的学习方式更为接近。小时候你妈妈不会看见一只狗就跟你说这是狗,而是其实在她告诉你之前你就能很明显分辨出狗和猫是不一样的,那么当她告诉你某一狗是狗,那么你就明白原来那些长这样的叫狗。所以人在学习时,自己会对看到的世界进行预处理,比如类比等等,而这些与无监督学习时非常接近的。
,是数据本身的概率分布。一般来说,无监督学习的概率密度函数是多变量的,而监督学习则是单变量的。无监督学习跟我们人的学习方式更为接近。小时候你妈妈不会看见一只狗就跟你说这是狗,而是其实在她告诉你之前你就能很明显分辨出狗和猫是不一样的,那么当她告诉你某一狗是狗,那么你就明白原来那些长这样的叫狗。所以人在学习时,自己会对看到的世界进行预处理,比如类比等等,而这些与无监督学习时非常接近的。
1.3.1 发现集群
这就是一个聚类问题,首先我们先看如下的图
先看左图,左图表示的是很多人的身高和体重的训练数据,我们要做的就是将数据分类,在无监督的学习中,我们并不知道要将数据分成几类,所以首先我们要去选择K,将数据分成K类。![]() 。在确定了K之后,我们接下来就是确定每一个样本点属于哪一类,如上图,比方说K确定后为2,那么假设
。在确定了K之后,我们接下来就是确定每一个样本点属于哪一类,如上图,比方说K确定后为2,那么假设![]() 的类别为
的类别为![]() ,那么
,那么![]() ,那么
,那么![]() 。
。
1.3.2 发现潜在的因素
现实中有很多的数据,看上去维度很高,但是实际上各维度之间具有比较强的相关性,对于这样的数据,我们可以通过降维的手段进行压缩。比如下图:
左边图显示数据是三维的,但是实际上我们发现其实数据几乎是在一个平面上的,这样原来由(x,y,z)表示的数据,在某组基下就可以用(m,n)来进行表示,这样就实现了降维。降维有很多好处,首先可以减少数据的储存空间,其次可以提高算法的效率,另外如果能将高位的数据压缩到三维一下,那么可以实现可视化,能够从更加直观的感受上去观察数据的分布。比如说文中关于人脸的例子,这是图像,数据上就是矩阵,我们对该矩阵进行奇异值分解,分别取前三个较大的奇异值,那么所看到的图像与原来的图像有很大的相似度,这就说明主要这三个维度就可以很好的刻画人的脸的大致形状。
主成分分析法(PCA,principle components analysis)是最常用的一个降维的方法。具体什么是主成分分析法,书籍后面会提到。
1.3.3 发现图的结构
这里就是我们会有一些变量,那么这些变量之间可能会有一些关联,那么这就涉及到图的概念,我们的目的就是从数据中,将这个图的结构给学习出来。![]() 。对于图结构的学习,主要就是两个方面的目的,一就是希望获得一些知识,知道哪些是相关的,另外一个方面则是为了实现更好的联合概率密度估计器,这一块我个人认为是与后面的图模型联系在一起,因为联合概率密度函数可以通过图模型表示。
。对于图结构的学习,主要就是两个方面的目的,一就是希望获得一些知识,知道哪些是相关的,另外一个方面则是为了实现更好的联合概率密度估计器,这一块我个人认为是与后面的图模型联系在一起,因为联合概率密度函数可以通过图模型表示。
1.3.4 矩阵填充
有的时候我们会丢失掉一些数据,或者说一些数据我们获得不了。那么这个时候我们要根据已有的数据对空缺的矩阵数据进行填充。接下来将会给出一些例子。
1.3.4.1 图像填充
如图所示,左边是一个被噪声污染了的,同时中间空了一块的图像。对于该图像的处理,首先需要对图像进行去噪,然后通过去噪之后的那些点,计算中间全黑的点的联合概率密度分布,然后通过MAP去得到每一个像素点的值,最终就可以恢复成(b)所展示的样子。
1.3.4.2 协同过滤
很典型的一个例子就是经常听到的关于电影的评价。因为每个人只是看了一部分的电影,所以如果把观众作为行,电影作为列,那么就会有一些数据是空缺的。那么如何得到观众关于没有看过电影的评价(可以作为电影推荐系统),就是一个矩阵填充问题。这个问题可以通过协同过滤的方法去求解。一般来说可以从两个方面去看待。一是找一个跟你的电影口味很接近的人,如果他喜欢看电影A,你没看过,那么你很大程度也会喜欢看A。二则是找跟你看过的电影很接近的电影,比如你喜欢看哈利波特,但是没有看过魔戒,但是这两个电影都是魔幻类电影,很接近,那么你很大程度上也会喜欢看魔戒。这就是协同过滤的基本思想。
1.3.4.3 购物篮分析
购物篮问题中,假设你做了N次购物,购买的物品总集合为![]() ,那么如果在第i次购物时你买了物品j,那么
,那么如果在第i次购物时你买了物品j,那么![]() 就为1。所以这样就构成了一个完全填充的
就为1。所以这样就构成了一个完全填充的![]() 矩阵。那么如果你又进行了一次购物,那么我们知道你购买了一部分商品,剩下的商品我们可以预测你可能还会购买其他的商品。这一点很容易理解,因为购物很多时候就是有相关联的,有些关联是我们很容易得到的,比如买了面包的人,往往也会买黄油。不过之前很多书上举了这个例子,就是国外男人在买纸尿布的时候会买啤酒。这就是从数据分析上得到的。从我们直观上其实不太好理解。
矩阵。那么如果你又进行了一次购物,那么我们知道你购买了一部分商品,剩下的商品我们可以预测你可能还会购买其他的商品。这一点很容易理解,因为购物很多时候就是有相关联的,有些关联是我们很容易得到的,比如买了面包的人,往往也会买黄油。不过之前很多书上举了这个例子,就是国外男人在买纸尿布的时候会买啤酒。这就是从数据分析上得到的。从我们直观上其实不太好理解。
文中最后还说了解决这样的问题在数据挖掘中,使用 frequent itemset mining,在本书中我们使用计算联合概率分布的方法。该书提到,在数据挖掘方向上呢,总是喜欢强调解释性的模型(更能让人理解的模型),但是在机器学习方面更强调的是精确的模型。
1.4 机器学习的一些基本概念
接下来会简单的介绍关于机器学习的一些基本的概念。
1.4.1 参数模型 vs 非参数模型
如果模型的参数不会随着数据量的增加而增加,那么就是参数模型(parametric model),如果模型的参数会随着数据量的增加而增加,那么称之为非参数模型(nonparametric model)。非参数模型相比而言更加的灵活,能够表现更加广泛的模型,但是随着数据量的增加,非参数模型的计算量会非常的大,所以两者各有优缺点。
1.4.2 一个简单的非参的分类器:K邻近
一个关于非参的简单的分类器就是K邻近(K nearest neighbor(KNN))分类器。先上个图,看图说话
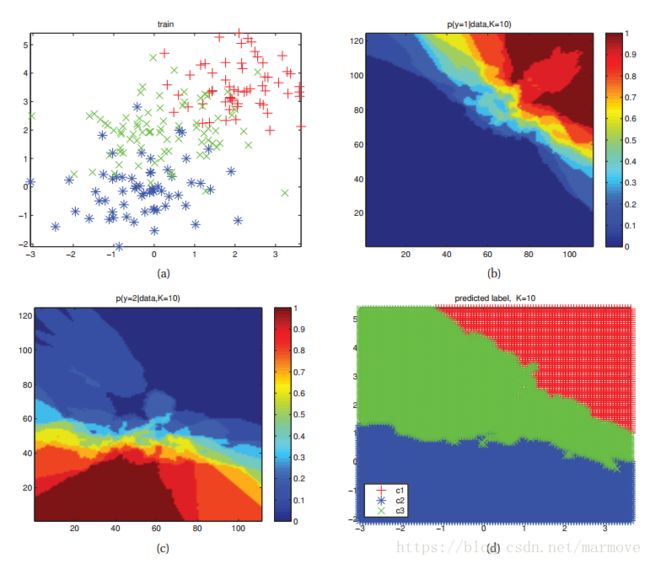
图(a)是训练数据,什么是K邻近算法呢,简单点说就是对于一个新的数据点![]() ,我们找K个离它最近的点,然后找出这K个点中,哪一个类别的数目最多,那么这个点
,我们找K个离它最近的点,然后找出这K个点中,哪一个类别的数目最多,那么这个点![]() 就属于哪一类。用公式来看呢,就是
就属于哪一类。用公式来看呢,就是
indices(![]() ) = 1如果
) = 1如果![]() ,否则为0。图(d)给出了根据该训练数据得到最终的划分。
,否则为0。图(d)给出了根据该训练数据得到最终的划分。
1.4.3 维度诅咒
KNN分类器,是一个非常好用的,简单的,性能也很好的分类器。但是这个分类器存在一个严重的问题,在输入数据的维度很高的时候,这个算法就会呈现很差的性能。假设我们现在数据的输入的维度是D = 10, 训练的数据均匀的分布在一个边长为1超正方体当中。那么如果我们想获得10%的数据,那么就是要获得0.1的体积。假设边长为e,![]() ,e = 0.8,在每一个维度上要拓展0.8的长度,即使是1%的数据,也要拓展0.63。这个算法看起来就不再那么紧。就是说我即使想要获得很少的数据,但是我在每天边上仍要扩展很长的距离。这样的点也就不是正真意义上的邻近。实际上你所找的那些邻近点,可能已经离你很远了。
,e = 0.8,在每一个维度上要拓展0.8的长度,即使是1%的数据,也要拓展0.63。这个算法看起来就不再那么紧。就是说我即使想要获得很少的数据,但是我在每天边上仍要扩展很长的距离。这样的点也就不是正真意义上的邻近。实际上你所找的那些邻近点,可能已经离你很远了。
1.4.4 分类和回归的参数模型
对于高维的问题呢,我们往往对于数据的分布做一些假设,这在参数模型上很容易看到。我个人的理解就是我们要对数据的分布做一些假设这样就能去压缩维度,比如我就假设是线性模型,那么无论你的输入维度多高,你的数据就是线性的,利用这个结构,维度的增加对算法的影响就是很微弱了。
1.4.5 线性回归
常见的最广泛的一个回归模型就是线性回归模型。一般可以写成如下的形式: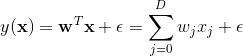 ,其中
,其中![]() 。
。![]() ,是一个残差项。对于该模型来说,参数就是
,是一个残差项。对于该模型来说,参数就是![]() 。
。![]() 那么从概率的角度来看,
那么从概率的角度来看,![]() 。这是基于
。这是基于![]() 的条件概率密度函数。如果参数得到了,那么y的分布就知道了。
的条件概率密度函数。如果参数得到了,那么y的分布就知道了。
对于这样的回归问题,![]() 可以用非线性的函数
可以用非线性的函数![]() 去代替。我们假设x是标量。那么
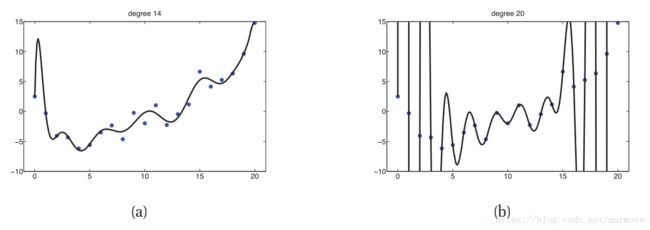
去代替。我们假设x是标量。那么![]() 可以是[
可以是[![]() ],下图分别给出了d等于14以及20的拟合情况。
],下图分别给出了d等于14以及20的拟合情况。
这个也称作多项式回归(polynomial regression)。当然还有很多其他的非线性函数,该书的后面会提到。
1.4.6 逻辑回归
对于线性回归我们做两点改变,第一点就是![]() ,这个式子表明y是服从均值为
,这个式子表明y是服从均值为![]() 的伯努利分布,而不是高斯分布了。第二点就是这里的
的伯努利分布,而不是高斯分布了。第二点就是这里的![]() 发生了改变,不再是
发生了改变,不再是![]() 而是sigm(
而是sigm(![]() )。sigm就是sigmoid函数。如果我们设置一个阈值,就可以作出最终的预测。比如
)。sigm就是sigmoid函数。如果我们设置一个阈值,就可以作出最终的预测。比如![]() 。下图给出sigmoid函数的样子,以及拟合的示例。
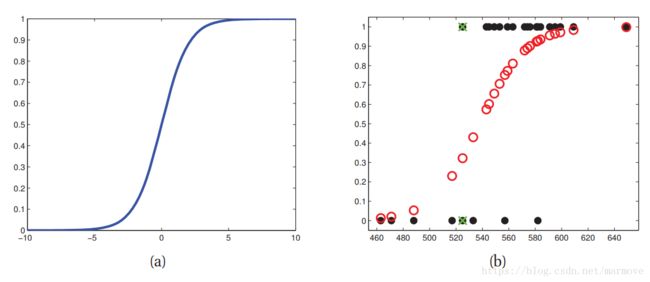
。下图给出sigmoid函数的样子,以及拟合的示例。
逻辑回归的训练样本其实在数据上很多时候不是线性可分的,所以即使针对训练数据也做不到0误差。在图(b)中找不到一条与y轴平行的线将数据0和1完全的分开。
1.4.7 过拟合
过拟合简单来说就是对训练数据的过度拟合,把训练数据自身带有的一些特殊性给带了进去,或者是噪声。就拿简单的线性回归来说,我们如果用多项式拟合,如1.4.5的(b)图,很明显,针对训练数据,这样训练出来的误差为0,但是明显这个模型完全不适用于其他的数据,这就是过拟合的典型。所以说不是越复杂的模型就越好,而是与数据越接近的模型才是最好的。过拟合典型的表现就是针对训练数据低偏差高方差。
1.4.8 模型选择
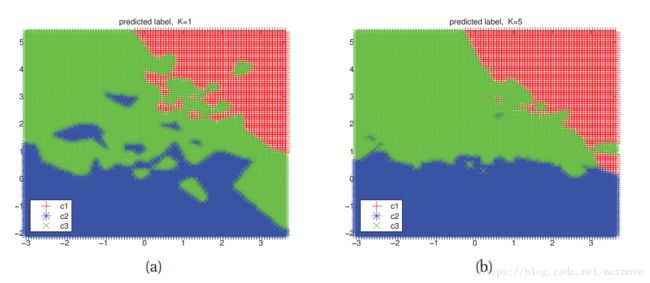
模型的选择是很重要的,就拿KNN来说,当K = 1时,那么经过划分后,每一个训练样本都是在正确的标签下,误差为0,但是很明显这不是最好的分类器,这明显过拟合了,但是如果加大K,那么如下图
K=5时明显划分的更加合理,但是这时候有一些训练样本在此划分下,就是错误的,很明显在蓝色的区域有几个绿色的叉,这就是训练样本中的点,这些点应该是蓝点。所以我们不能用训练样本来评判误差。这时候就提到了模型的泛化误差(generalization error)和测试集(test set)。泛化误差是通过训练集合得到的。这才是我们真正需要关注的。如下图:
、
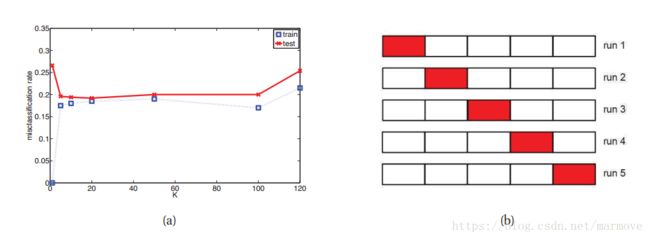
根据图(a),我们发现在训练误差很小的时候K=1,但是测试误差很大,这个时候是处于过拟合状态。K在10到100之间的取值都是含可以接受的。当K很大时,训练误差和测试误差都很大,这是处于欠拟合的状态。
但是在实际当中我们并没有测试数据,我们只是给了一堆训练数据,让你给出模型。这时候我们需要将训练数据分为两个部分:训练集和验证集,训练集用来进行训练,验证集用来进行模型的选择。一般来说80%作为训练用,20%作为验证集。但是当数据量很少的时候,这又出现问题,如果验证集数据少了,那么这个验证结果是否可靠。如果训练集少了,那么这个训练集能否表征整个数据集的特征。这是个矛盾。这时候我们采用交叉验证法。把数据分为K类,如图(b)所示,每一次用其中的K-1类进行训练,剩下的那一类作为验证集进行测试。总共跑K次,取平均误差,进行模型的选择。
1.4.9 没有免费午餐理论(NFL,no free lunch theorem)
该理论就是说没有最好的模型,在有些假设下,这个模型是好的,但是在其他的假设下那个模型又会更好。所以我们要根据现实意义以及数据的特殊性,制定相应的算法。关于这一点,在周志华的西瓜书中给出了概率意义上的特殊情况的证明,有兴趣的可以去看一下。