算法图解-广度优先算法
Introduction:
在基于图的操作中,如果需要统计A到B的最短路径,广度优先是比较合适的算法。
首先看图:
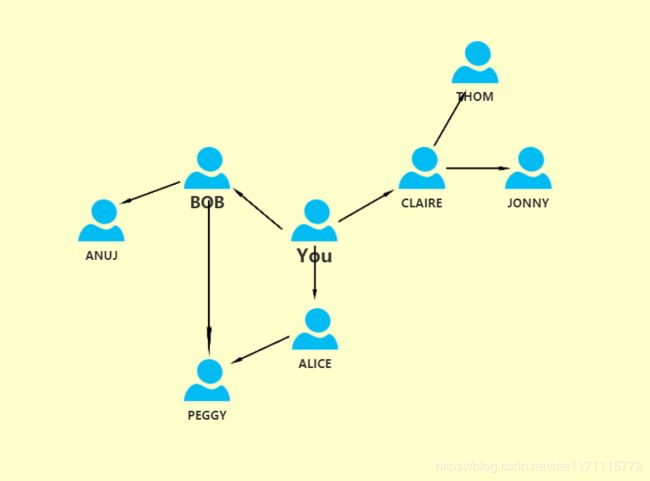
我们需要从You开始,从You的每一层关系开始查找,知道找到经销商开始。假设经销商是THOM?
这是一个有三层关系的图,其中You、BOB、ALICE是其中的节点,而You->ALICE这样的就是其中的边,这样对于You,他的关系有:
You->BOB,You->ALICE,You->CLAIRE,在Python中,使用散列表可以描述对应的关系。
表示这种映射关系的Python代码如下:
graph={} #先创建一个散列表 或者使用 graph=dict()
graph["you"]=["ALICE","BOB",CIAIRE"]
使用Python表示完整的图:
graph={} #先创建一个散列表 或者使用 graph=dict()
graph["you"]=["ALICE","BOB",CIAIRE"]
graph["BOB"]=["ANUJ","PUGGY"]
graph["ALICE"]=["PEGGY"]
graph["CLAIRE"]=["THOM","JONNY"]
graph["ANUJ"]=[]
graph["PEGGY"]=[]
graph["THOM"]=[]
graph["JONNY"]=[]
Tips:对于程序而言,键-值的添加顺序重要吗?比如使用graph["you"]=["BOB",CIAIRE"."ALICE"]会对结果产生影响吗?
Answer:因为散列表是无序的,换言之键值对的顺序也是无序的,所以对程序而言没有什么影响。
Achieve:
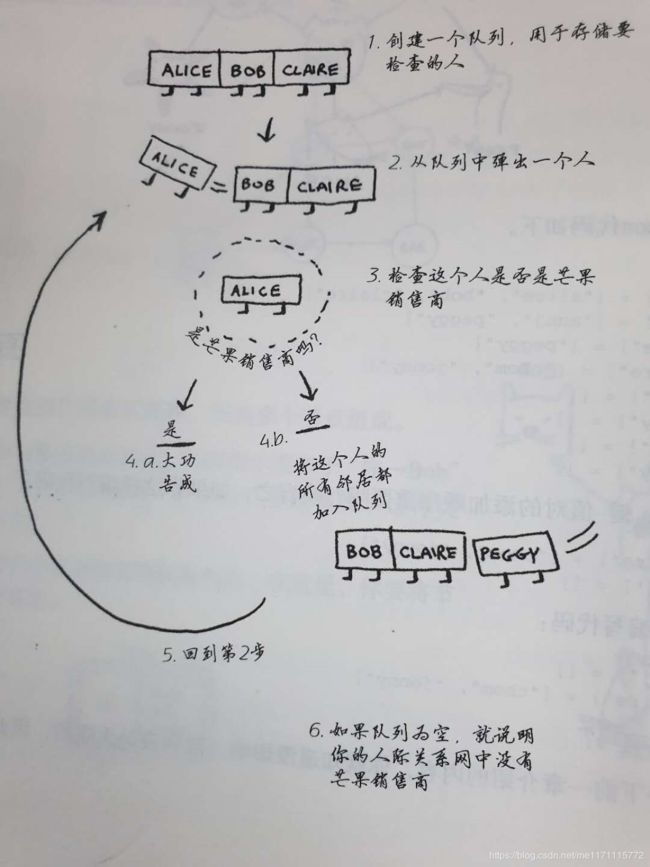
简单通过图片描述一下算法的工作原理:
直接放上书中的图:
在使用广度优先算法时,需要创建一个额外队列用于保存哪些节点被检索了,哪些没有,在python中,可以使用deque来创建一个双端队列,可以实现入队出队操作。
from collections import deque
search_queue = deque () #新建一个队列
search_queue += graph["You"] #将You的三个邻居添加到队列里面
下面看看其他的代码
while search_queue: #search_queue是一个队列,主要队列有数据就往下执行
person = search_queue.popleft() #取出其中的一个人
if person_is_seller(seller): #检查这个人是否是经销商
print person + "is a mango seller !" #如果是,就打印 然后结束程序
return True
else:
search_queue += graph [person] #不是经销商,就把他的朋友都加入队列
return False #如果所有的都不是经销商,返回并退出
在上述的代码中,person_is_seller(name)是一个未定义的函数,咱们需要自己定义
def person_is_seller(name):
return name== "THUM"
Tips:这个代码中有个问题,在上面的图中,PEGGY跟两个人有关系,所以如果使用上述代码,PEGGY会被重复检查,这样相当于做了无用功,在一个数据较多的程序中,我们需要避免这种情况的发生,我们可以:
创建一个已检索人的队列,每次检索这个人的时候,看一下已检索人队列是不是已经有这个人,如果有了就不需要检索了,如果没有,检查这个人,然后把这个人加到已检索人队列。
当然在这个例子中,我们已知了重复为一个,对于这个例子,每次检查避免重复带来的效益不是太高,不过这种检查的思想是需要具备的。
运行时间:
单从边数来讲,运行时间最多为O(边数)
但是我们还添加了另外一个队列,用来检索已经检查过的人,所以在队列中添加人的操作时间复杂度为O(1),因此添加人需要的总时间数为O(人数),两者结合起来,总的时间就是O(人数+边数),记作O(V+E),其中V为vertice。
Reflect:
1 在这个算法中,有什么可以优化的地方?
2 出了上述程序会重复检索这个不足之外,是否有其他的不足?