算法复杂度分为时间复杂度和空间复杂度,一个好的算法应该具体执行时间短,所需空间少的特点。
随着计算机硬件和软件的提升,一个算法的执行时间是算不太精确的。只能依据统计方法对算法进行估算。我们抛开硬件和软件的因素,算法的好坏直接影响程序的运行时间。
我们看一下小例子:
int value = 0; // 执行了1次
for (int i = 0; i < n; i++) { // 执行了n次
value += i;
}
这个算法执行了 1 + n 次,如果n无限大,我们可以把前边的1忽略,也就是说这个算法执行了n次
时间复杂度常用大O符号表示,这个算法的时间复杂度就是O(n).
概念: 一般情况下,算法的基本操作重复执行的次数是模块n的某一函数f(n),因此,算法的时间复杂度记做 T(n) = O(f(n))。 随着模块n的增大,算法执行的时间增长率f(n)的增长率成正比,所以f(n)越小,算法 的时间复杂度越低,算法的效率越高。
计算时间复杂度
1.去掉运行时间中的所有加法常数。
2.只保留最高阶项。
3.如果最高阶项存在且不是1,去掉与这个最高阶相乘的常数得到时间复杂度
我们看一个例子
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
// do .....
}
}
当 i = 0 时 里面的fo循环执行了n次,当i等待1时里面的for循环执行了n - 1次,当i 等于2里里面的fro执行了n - 2次........所以执行的次数是
根据我们上边的时间复杂度算法
1.去掉运行时间中的所有加法常数: 没有加法常数不用考虑
2.只保留最高阶项: 只保留
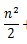
3. 去掉与这个最高阶相乘的常数: 去掉
 只剩下
只剩下
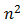
最终这个算法的时间复杂度为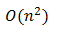
再看一个线性的
for ( int i = 0; i < n; i++) {
// do .....
}
因为循环要执行n次所以时间复杂度为O(n)
其它的我也就不一个一个算了,下面给出了常用的时间复杂度
| 排序法 |
最差时间分析 | 平均时间复杂度 | 稳定度 | 空间复杂度 |
| 冒泡排序 | O(n2) | O(n2) | 稳定 | O(1) |
| 快速排序 | O(n2) | O(n*log2n) | 不稳定 | O(log2n)~O(n) |
| 选择排序 | O(n2) | O(n2) | 稳定 | O(1) |
| 二叉树排序 | O(n2) | O(n*log2n) | 不一顶 | O(n) |
| 插入排序 |
O(n2) | O(n2) | 稳定 | O(1) |
| 堆排序 | O(n*log2n) | O(n*log2n) | 不稳定 | O(1) |
| 希尔排序 | O | O | 不稳定 | O(1) |
