mosquito_zm
mosquito_zm

01分数规划入门

01分数规划是这样的一类问题，有一堆物品，每一个物品有一个收益ai，一个代价bi，我们要求一个方案使选择的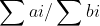\sum{ai}/\sum{bi}最大。

首先我们来一道例题吧，01分数规划的大体方法都是一样的。

友情提示：poj请选择C++提交，g++提交的话容易作死（poj的g++要用%f输入输出double，pojC++用%lf）

例1 Dropping Tests poj2976

给出n个物品，每个物品有两个属性a和b，选择n-k个元素，询问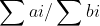\sum{ai}/\sum{bi}的最大值。

1<=n<=1000，0<=k

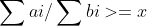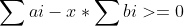首先这题显然是兹磁二分的，而\sum{ai}/\sum{bi}>=x就等价于\sum{ai}-x*\sum{bi}>=0。

所以我们发现二分完把ai-x*bi排序后把最大的n-k个选出来就行了。

复制代码 
#include 
#include 
#include 
#include 
#include <string.h>
#include 
#include 
#include 
#include <set>
#include 
using namespace std;
int n,k,a[2333],b[2333];
double ps[2333];
bool ok(double x)
{
    for(int i=1;i<=n;i++) ps[i]=a[i]-x*b[i];
    sort(ps+1,ps+1+n);
    double ans=0;
    for(int i=n;i>=k+1;i--) ans+=ps[i];
    return ans>=0;
}
void sol()
{
    for(int i=1;i<=n;i++) scanf("%d",a+i);
    for(int i=1;i<=n;i++) scanf("%d",b+i);
    double l=0,r=1;
    while(r-l>1e-6)
    {
        double mid=(l+r)/2;
        if(ok(mid)) l=mid; else r=mid;
    }
    printf("%.0lf\n",l*100);
}
int main()
{
    while(scanf("%d%d",&n,&k),n|k) sol();
}
复制代码

但是还有一种神奇的做法，既然我们可以二分一个值，而且得出一个更优的解，那么我们就可以在这个解的基础上继续做，直到满足精度。

复制代码 
#include 
#include 
#include 
#include 
#include <string.h>
#include 
#include 
#include 
#include <set>
#include 
using namespace std;
int n,k;
struct pro {double a,b,p;}s[233333];
bool operator < (pro a,pro b) {return a.p<b.p;}
double sol(double x)
{
    for(int i=1;i<=n;i++) s[i].p=s[i].a-x*s[i].b;
    sort(s+1,s+1+n);
    double aa=0,bb=0;
    for(int i=n;i>=k+1;i--) aa+=s[i].a,bb+=s[i].b;
    return aa/bb;
}
void sol()
{
    for(int i=1;i<=n;i++) scanf("%lf",&s[i].a);
    for(int i=1;i<=n;i++) scanf("%lf",&s[i].b);
    double l=0,ans=0;
    do
    {
        l=ans; ans=sol(ans);
    }while(fabs(l-ans)>1e-6);
    if(l>1) l=1;
    if(l<0) l=0;
    printf("%.0lf\n",l*100);
}
int main()
{
    while(scanf("%d%d",&n,&k),n|k) sol();
}
复制代码

例2 Desert King poj2728

（模型有转化）

给出一个n个点的完全图，每条边有两个权值cost和len。

求一个生成树使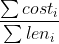\frac{\sum{cost_i}}{\sum{len_i}}最小。

2<=n<=1000

还是二分答案x，把每条边边权设为cost-x*len，跑最小生成树，判答案的正负。建议用prim跑，复杂度比较科学。

复制代码 
#include 
#include 
#include 
#include 
#include <string.h>
#include 
#include 
#include 
#include <set>
#include 
using namespace std;
typedef long double ld;
#define SZ 1066
int n,xx[SZ],yy[SZ],hh[SZ],fm[SZ];
bool del[SZ];
ld mind[SZ],d[SZ][SZ],d1[SZ][SZ],d2[SZ][SZ];
ld sqr(ld x) {return x*x;}
ld Abs(ld x) {return (x>=0)?x:-x;}
bool ok(ld x)
{
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++) d[i][j]=d1[i][j]-x*d2[i][j];
    }
    for(int i=0;i<=n;i++) mind[i]=1000000000, del[i]=0;
    mind[1]=0; fm[1]=0;
    ld ans=0;
    for(int i=1;i<=n;i++)
    {
        int mp=0;
        for(int j=1;j<=n;j++)
        {
            if(mind[j]j;
        }
        ans+=d[fm[mp]][mp]; del[mp]=1;
        for(int j=1;j<=n;j++)
        {
            if(d[mp][j]>=mind[j]||del[j]) continue;
            mind[j]=d[mp][j]; fm[j]=mp;
        }
    }
    return ans<=0;
}
void sol()
{
    for(int i=1;i<=n;i++) scanf("%d%d%d",xx+i,yy+i,hh+i);
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            d1[i][j]=Abs(hh[i]-hh[j]);
            d2[i][j]=sqrt(sqr(xx[i]-xx[j])+sqr(yy[i]-yy[j]));
        }
    }
    ld l=0,r=1000000000;
    while(r-l>1e-6)
    {
        double mid=(l+r)/2;
        if(ok(mid)) r=mid; else l=mid;
    }
    printf("%.3lf\n",(double)l);
}
int main()
{
    while(scanf("%d",&n),n) sol();
}
复制代码

直接迭代

复制代码 
#include 
#include 
#include 
#include 
#include <string.h>
#include 
#include 
#include 
#include <set>
#include 
using namespace std;
#define SZ 1066
int n,xx[SZ],yy[SZ],hh[SZ],fm[SZ];
bool del[SZ];
double mind[SZ],d[SZ][SZ],d1[SZ][SZ],d2[SZ][SZ];
double sqr(double x) {return x*x;}
double Abs(double x) {return (x>=0)?x:-x;}
double sol(double x)
{
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++) d[i][j]=d1[i][j]-x*d2[i][j];
    }
    for(int i=0;i<=n;i++) mind[i]=1000000000, del[i]=0;
    mind[1]=0; fm[1]=0;
    double aa=0,bb=0;
    for(int i=1;i<=n;i++)
    {
        int mp=0;
        for(int j=1;j<=n;j++)
        {
            if(mind[j]j;
        }
        aa+=d1[fm[mp]][mp];
        bb+=d2[fm[mp]][mp];
        del[mp]=1;
        for(int j=1;j<=n;j++)
        {
            if(d[mp][j]>=mind[j]||del[j]) continue;
            mind[j]=d[mp][j]; fm[j]=mp;
        }
    }
    return aa/bb;
}
void sol()
{
    for(int i=1;i<=n;i++) scanf("%d%d%d",xx+i,yy+i,hh+i);
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            d1[i][j]=Abs(hh[i]-hh[j]);
            d2[i][j]=sqrt(sqr(xx[i]-xx[j])+sqr(yy[i]-yy[j]));
        }
    }
    double l,ans=0;
    do{ans=sol(l=ans);}while(fabs(l-ans)>1e-6);
    printf("%.3lf\n",l);
}
int main()
{
    while(scanf("%d",&n),n) sol();
}
复制代码

例3 Sightseeing Cows poj3621

给出一个有L个点P条边的有向图，每个点上有点权F，每条边上有边权T。

求一个回路使\frac{\sum{F_i}}{\sum{T_i}}最大。

2<=L<=1000，2<=P<=5000。

因为环上边和点数相等，我们可以直接把边权当做花费，入点的点权当作收入。

然后还是二分答案建图，判图中有没有正环。取个反就成了判负环。

dfs版spfa即可。

复制代码 
#include 
#include 
#include 
#include 
#include <string.h>
#include 
#include 
#include 
#include <set>
#include 
using namespace std;
#define SZ 666666
int n,m,v[SZ],fst[SZ],vb[SZ],nxt[SZ],vc[SZ],M=0,X;
bool vis[SZ],fh=0;
double dist[SZ];
void adde(int a,int b,int c) {++M; nxt[M]=fst[a]; fst[a]=M; vb[M]=b; vc[M]=c;}
void dfs(int p,double x)
{
    vis[p]=1;
    for(int e=fst[p];e;e=nxt[e])
    {
        double C=v[vb[e]]-x*vc[e];
        if(dist[vb[e]]>=C+dist[p]) continue;
        if(vis[vb[e]]) {fh=1; return;}
        dist[vb[e]]=C+dist[p];
        dfs(vb[e],x);
        if(fh) return;
    }
    vis[p]=0;
}
bool ok(double x)
{
    for(int i=1;i<=n;i++) vis[i]=dist[i]=0;
    fh=0;
    for(int i=1;i<=n;i++)
    {
        dfs(i,x);
        if(fh) return 1;
    }
    return 0;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%d",v+i);
    for(int i=1;i<=m;i++)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        adde(a,b,c);
    }
    double l=0,r=1000000000;
    while(r-l>1e-6)
    {
        double mid=(l+r)/2;
        if(ok(mid)) l=mid; else r=mid;
    }
    printf("%.2lf\n",l);
}
复制代码
迭代的话…似乎不太好写，就算了吧

你可能感兴趣的:(acm,数学,acm)

  • Python数据分析与可视化实战指南 William数据分析 pythonpython数据
    在数据驱动的时代，Python因其简洁的语法、强大的库生态系统以及活跃的社区，成为了数据分析与可视化的首选语言。本文将通过一个详细的案例，带领大家学习如何使用Python进行数据分析，并通过可视化来直观呈现分析结果。一、环境准备1.1安装必要库在开始数据分析和可视化之前，我们需要安装一些常用的库。主要包括pandas、numpy、matplotlib和seaborn等。这些库分别用于数据处理、数学
  • 398顺境，逆境 戴骁勇
    2018.11.27周二雾霾最近儿子进入了一段顺境期，今天表现尤其不错。今天的数学测试成绩喜人，没有出现以往的计算错误，整个卷面书写工整，附加题也在规定时间内完成且做对。为迎接体育测试的锻炼有了质的飞跃。坐位体前屈成绩突飞猛进，估测成绩能达到12cm，这和上次测试的零分来比，简直是逆袭。儿子还在不断锻炼和提升，唯恐到时候掉链子。跑步姿势在我的调教下，逐渐正规起来，速度随之也有了提升。今晚测试的50
  • 没想到，真没想到 一棵落花的树
    生活中，每一件小事都蕴藏着他的道理。有些令你意外，却能让你收到更为意外的结果。那一次，我真没想到的事，让我收获了爱。记忆的雨飘落下来，扰乱了我平静的心湖。那是一次数学考试，我破天荒地考了“99”分。我不禁沾沾自喜，这成绩我可不容易得到，妈妈一定会好好表扬我的。回到家，我想妈妈得意的报出成绩，妈妈只是淡淡的说：“嗯，等会儿试卷拿给我看看。”做完作业，我把试卷拿给了妈妈。只见妈妈捧着试卷，眯着眼睛盯着
  • Python开发常用的三方模块如下： 换个网名有点难 python开发语言
    Python是一门功能强大的编程语言，拥有丰富的第三方库，这些库为开发者提供了极大的便利。以下是100个常用的Python库，涵盖了多个领域：1、NumPy，用于科学计算的基础库。2、Pandas，提供数据结构和数据分析工具。3、Matplotlib，一个绘图库。4、Scikit-learn，机器学习库。5、SciPy，用于数学、科学和工程的库。6、TensorFlow，由Google开发的开源机
  • 最超值的Mac——Mac mini 初心么么哒
    你知道最超值的Mac是什么吗？自2005年以来，Macmini一直是Apple台式机产品线中的主要产品。最初推出是为了让对Mac好奇的Mac进入Apple生态系统的一种简单方式，现在新的AppleSiliconMacmini可能是任何寻找新Mac的人的最有吸引力的购买。什么是AppleSiliconMacmini？M1Macmini是Apple最小的台式电脑，同时也是最快的台式电脑之一。最新型号由
  • C语言 判断回文数 Y雨何时停T c语言学习
    一，回文数概念“回文”是指正读反读都能读通的句子，它是古今中外都有的一种修辞方式和文字游戏，如“我为人人，人人为我”等。在数学中也有这样一类数字有这样的特征，成为回文数。设n是一任意自然数。若将n的各位数字反向排列所得自然数n1与n相等，则称n为一回文数。例如，若n=1234321，则称n为一回文数；但若n=1234567，则n不是回文数。二，判断回文数实现思路一：数组与字符串将数字每一位按顺序放
  • 九月班级管理工作反思 追梦蜂
    这个月应该算是最难的一个月，我已N年没当班主任，然后我又开始当了。职称是一方面，想到我如果退休了，不能再接触学生了，那该是多么遗憾的事！我的学生梁*铭是我的榜样，她那么努力，那么拼，那么上进，为什么我不行？虽然我面临的工作很难，但是高考数学也不容易。她拿下来了！满分150分她考了146分！我目睹她的艰辛，她的拼搏！还有，我要为我的孩子做榜样，如何竭尽全力，实现梦想。还有，服务，为社会做事，也是会有
  • 2019考研 | 西交大软件工程 笔者阿蓉
    本科背景：某北京211学校电子信息工程互联网开发工作两年录取结果：全日制软件工程学院分数：初试350+复试笔试80+面试85+总排名：100+从五月份开始脱产学习，我主要说一下专业课和复试还有我对非全的一些看法。【数学100+】张宇，张宇，张宇。跟着张宇学习，入门视频刷一遍，真题刷两遍，错题刷三遍。书刷N多遍。从视频开始学习，是最快的学习方法。5-7月份把主要是数学学好，8-9月份开始给自己每个周
  • 3.增删改查--连接查询 问女何所忆
    关系型数据库的一个特点就是，多张表之间存在关系，以致于我们可以连接多张表进行查询操作，所以连接查询会是关系型数据库中最常见的操作。连接查询主要分为三种，交叉连接、内连接和外连接，我们一个个说。1、交叉连接交叉连接其实连接查询的第一个阶段，它简单表现为两张表的笛卡尔积形式，具体例子：如果你没学过数学中的笛卡尔积概念，你可以这样简单的理解这里的交叉连接：两张表的交叉连接就是一个连接合并的过程，T1表中
  • 高级UI<第二十四篇>：Android中用到的矩阵常识 NoBugException
    （1）定义在数学中，矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合。由m×n个数aij排成的m行n列的数表称为m行n列的矩阵，简称m×n矩阵。记作：图片.png这m×n个数称为矩阵A的元素，简称为元，数aij位于矩阵A的第i行第j列，称为矩阵A的(i,j)元，以数aij为(i,j)元的矩阵可记为(aij)或(aij)m×n，m×n矩阵A也记作Amn。元素是实数的矩阵称为实矩阵，元素是复
  • 感恩日记Day 236 E姐小酒窝
    图片发自App1.感谢16愿意听我"唠叨"，人与人的信任和托付在此刻弥足珍贵珍贵；2.感谢到家就能吃上美味的中餐，辛苦妞爸；3.感谢妞中午愿意听我叼叼旅行中的事儿；4.感谢星巴克就在家附近，让我一杯回魂；5.感谢美妞总结我和爸爸优点并说两者揉和就很棒了。6.感谢看到妞第一天数学成绩后淡定的自己；将责任归回妞自己并总结行动。7.感谢林姐姐信任，又定变啦减脂套餐。8.感谢梅姐知道我旅行回来后约我吃饭；
  • 【高中数学/三角函数/判别式法求极值】已知：实数a,b满足a^2/4-b^2=1 求：3a^2+2ab的最小值 普兰店拉马努金 高中数学之三角函数高中数学三角函数判别式
    【问题】已知：实数a,b满足a^2/4-b^2=1求：3a^2+2ab的最小值【来源】App"网易新闻"中up主“我服子佩”的数学视频专辑，据其称是北京市某年的竞赛题。【解答】由a^2/4-b^2=1，联想到secθ^2-tanθ^2=1故设a/2=1/cosθ,b=sinθ/cosθ将a=2/cosθ,b=sinθ/cosθ代入3a^2+2ab得f(θ)=(12+4sinθ)/(1-sinθ^2
  • 2024年华为杯数学建模研赛C题思路代码+论文助攻 DS数模 2024华为杯数学建模华为2024华为杯2024研究生数学建模2024研赛
    2024年华为杯研究生数学建模竞赛（以下简研赛）将于9月21日上午8时正式开始。下文包含：2024研赛思路解析、研赛参赛时间及规则信息说明、好用的数模技巧及如何备战数学建模竞赛C君将会第一时间发布选题建议、所有题目的思路解析、相关代码、参考文献、参考论文等多项资料，帮助大家取得好成绩。2024年研赛将于9月21日上午8时正式开始这里有些资料，大家可以看看：【2024最全国赛研赛数模资料包】C君珍贵
  • 2021-10-17(376) 刘玥上学记
    今天早上妈妈六点就把我喊起来了，天气太冷了，姥姥给我们煮了鸡蛋，路上保暖用一切按部就班的进行，到公司刚刚好七点五十妈妈给我安排的是上午两张试卷，下午两张试卷上午的没做完，下午的我实在是不想做了，后来凯丽姐姐说早点写完，可以早些玩耍我就回办公室写作业了一直到下午四点半，凯丽姐姐过来检查，数学卷子还没做完询问了半天，原来是乘法口诀没有背过，然后凯丽姐姐就一个一个的给我提问而且还说让我晚上回去自己再重新
  • 2021-10-03 虫虫新生111
    今天放假的第3天感觉过得好快，总体来说数学做了25道题，里边有几道题还是弄得不清楚，仍然不懂怎么做，不过整体感觉思路比去年要清晰很多，因为有去年的基础，今年还是比较轻松一些。逻辑做了有几道题，6题，错2，有些概念总的是模糊不清，还是要反复的再整理一下概念，以及回头看一下讲的基础知识，把基础的公式弄懂才可以。现在困了睡觉，明天早点起床。
  • 七.正则化 愿风去了
    吴恩达机器学习之正则化（Regularization）http://www.cnblogs.com/jianxinzhou/p/4083921.html从数学公式上理解L1和L2https://blog.csdn.net/b876144622/article/details/81276818虽然在线性回归中加入基函数会使模型更加灵活，但是很容易引起数据的过拟合。例如将数据投影到30维的基函数上，模
  • 腾讯发表多模态综述，一文详解多模态大模型 存内计算开发者社区 多模态大模型人工智能chatgptAIGC量子计算AI-nativegptagi
    多模态大语言模型（MLLM）是近年来兴起的一个新的研究热点，它利用强大的大语言模型作为大脑来执行多模态任务。MLLM令人惊讶的新兴能力，如基于图像写故事和无OCR的数学推理，在传统方法中是罕见的，这表明了一条通往人工通用智能的潜在道路。在本文中，追踪多模态大模型最新热点，讨论多模态关键技术以及现有在情绪识别上的应用。腾讯AILab发表了一篇关于多模态大模型的最新综述《MM-LLMs:RecentA
  • 创设问题情境的策略 平常心666
    创设情境要有情趣案例：可以圈多少地如何让孩子喜欢数学，是数学教师必须思考和解决的问题。有趣的情境会吸引学生，使学生主动走近数学学习。因此，教师要结合学生的年龄特点和实际生活，创造出富有数学情趣的情境。创设情境要有生活案例：克与千克的生活情境正如著名数学家华罗庚所说：“宇宙之大，粒子之微，火箭之速，化工之巧，地球之变，日月之繁，无处不用数学。”数学与现实生活有着密切的联系。创设情境要有问题案例：喝出
  • 丁俊贵之《“女人和男人”那些事》 兴时态_198812
    【“女人和男人”那些事】生活中，我们经常用性别来给很多现象和问题贴标签。比如：女性发脾气是常见的事情，所以不要跟她们讲道理，要让着她们；女性考虑问题总是比较感性，不如男性那么理性、严谨、全面；女生的数学成绩普遍比较差，因此选文科的女生更多；……许许多多像这样的认知，已经成为我们根深蒂固的信念。我们在生活中哪怕不会直接这样讲，但多多少少都会有类似的想法和感受，并且用这些信念去理解和认知他人。一、人世
  • MATLAB语言基础教程、 小项目1：简单的计算器、 小项目2：有页面的计算器、使用App Designer创建GUI计算器 azuredragonz 学习教程matlab开发语言
    MATLABMATLAB语言基础教程1.MATLAB简介2.基本语法变量与赋值向量与矩阵矩阵运算数学函数控制流3.函数4.绘图案例：简单方程求解小项目1：简单的科学计算器功能代码项目说明小项目2：有页面的计算器使用AppDesigner创建GUI计算器主要步骤：完整代码（使用MATLAB编写）说明：如何运行：小项目总结MATLAB语言基础教程1.MATLAB简介MATLAB（矩阵实验室）是一种用于
  • 搞笑的数学老师 鹿悦
    今天,陈老师来到了我们班,我们都一脸闷闷不乐的写着家庭作业。陈老师一提到回答问题,我们的脸都快要掉到抽屉里了。"小牛，你来回答一下这道题。"突然，我们班都安静的鸦雀无声，紧接着一阵哄堂大笑的声音在班里回荡着。我们都说陈老师很有意思：史卓听就叫小史，曲子昱就叫小曲，朱宇豪就叫小朱，于恩智就叫小于。至于我呀，陈老师经常叫我小佑或者小张2号。（因为班里有许多姓张的同学）。我们都非常喜欢这个风趣幽默的陈老
  • 希希~嗯嗯~ 猪猪女孩小哒哒
    电话铺垫无聊天当天来上课的情况：外婆陪三岁的希希，妈妈陪小的大的上课规则感建立的还算不错，二的满场跑完全坐不住妈妈想找外教早教机构，因为大的在托班，里面会有数学、外教等分支教学课程。老二妈妈没怎么带教二宝。妈妈想给她找语言妈妈问有没有英文我的回答是英文课会有中教，应该回答中外教一起妈妈夸赞宝宝10个月会走了，今天见到的情形是宝宝走几步路就会跌倒，没有联系过爬，就开始走，长大以后模仿别人动作上面做的
  • 如何做好人生的选择题？百科全书式天才——赫伯特·西蒙给你答案 伽马有话说
    赫伯特·西蒙是谁？想必知道的人非常少。但当看到他的履历后，相信没有人再怀疑他是个“天才”。西蒙出生于1916年6月15日，是个美国人，他的名字全称为赫伯特·亚历山大·西蒙，在2001年2月9日与世长辞，在这84年的岁月中，西蒙以27岁时取得的政治学博士学位为开端，先后步入了政治学、管理学、认知心理学、信息科学、人工智能、科学哲学、应用数学、统计学、运筹学、控制论、数理经济学、公共管理等领域，在这些
  • 5/3亲子践行 豆果妈
    90天打卡累计天数：53/90#宣言（做好当知当觉的父母，处理情绪是第一步）#孩子第一个30天目标：每晚21:45前睡觉家长第一个30天目标：每晚23:00前睡觉加油小宝（黄唯嘉+10岁）践行打卡53/901.早睡早起：22：30-8：302.先吃青蛙：13.️今日闪光点：（1）早晨和爸爸一起去晨跑（2）上午带弟弟，陪弟弟玩了一个上午（3）下午完成了部分作业，还剩数学卷和采访小报#父母教练检视#孩
  • 科普阅读两不误，这才是儿童科普阅读的正确打开方式 麦麦安
    "孩子数学不好，根源在于语文没学好"，这一观点已经被越来越多的老师和家长接受。虽然阅读理解力看上去只和语文有关，事实上，它是所有学科的根基。比如一道数学应用题，只有正确地看懂了各种条件，才能把答案快速地解出来。在美国的小学教育体系中，很重要的一项任务是帮助儿童进行大量阅读，从而培养出理解及思考的能力。这种说法虽然正确，但很多孩子也会存在这样一个问题：绘本故事类的阅读量不小，看小说听故事几乎可以独立
  • 洛谷P1719 最大加权矩形 0hang 算法c++开发语言
    洛谷P1719最大加权矩形题目描述为了更好的备战NOIP2013，电脑组的几个女孩子LYQ,ZSC,ZHQ认为，我们不光需要机房，我们还需要运动，于是就决定找校长申请一块电脑组的课余运动场地，听说她们都是电脑组的高手，校长没有马上答应他们，而是先给她们出了一道数学题，并且告诉她们：你们能获得的运动场地的面积就是你们能找到的这个最大的数字。校长先给他们一个n\timesnn×n矩阵。要求矩阵中最大加
  • Tor Browser配置方法 淡水猫. 网络安全服务器
    密码学中有两种常见的加密方式：对称加密：加密和解密使用同一个秘钥，如AES、DES等算法。非对称加密：加密和解密使用不相同的密钥，这两个秘钥分别称为公钥（publickey）和私钥（privatekey）——也就是说私钥可以解开公钥加密的数据，反之亦然（很神奇的数学原理）。Tor是一个三重代理（也就是说Tor每发出一个请求会先经过Tor网络的3个节点），其网络中有两种主要服务器角色：中继服务器：负
  • 晚托第34天 唐锐_32c4
    2019-04-06本来担心优的抄写的作业不能及时完成，今天一来看到她写的作业后我放心多了。英语抄写的是满满的6面，说明你在老家期间没有耽误学习，自觉性有了提高。以后在学校期间不能吃外面小摊子的东西，防止有害细菌进入体内。杨今天表现的一般，数学计算能手只刷了3面，就开始骄傲，当我告诉你别人已经刷上几十面时你目瞪口呆。所以，以后一定要谦虚谨慎，人外有人，天外有天，始终有强悍的孩子远远超过你，你要做的
  • 第一次参加女儿的家长会 章章2021
    说来惭愧，从幼儿园到现在，第一次去参加女儿的家长会。老师们说了一下每个孩子在学校的表现。女儿被两位老师表扬语文老师:作业完成很好，错了及时订正，上课积极发言。数学老师:非常爱思考，责任感很强，爱卫生。回来把老师的表扬一五一十的传达给女儿，甚至有些地方还添油加醋了，哈哈。女儿上小学以来，基本没有操过什么心，作业，阅读，基本都能独立完成。平时聊天会强调班集体，也会多说老师的好话。女儿酷爱漫画书和绘本，
  • 架构师备考的一些思考（四） kiba518
    前言对于数学，我们之前学的是对的，但不是真的，所以我们没有数学思维。对于计算机，我们学校教的是对的，但不是真的，所以仅仅从学校学习知识的应届毕业生，不论985,211，本科，专科都一样，都是一张白纸，啥也不会。案例分析案例分析是5选3，第一题必答。问题一的类型架构风格对比问题二的类型质量属性填写问题三的类型ER图分析问题类型四场景分析，此类型题比较多。案例分析主要是结合我们之前介绍的内容和自身的经
  • HttpClient 4.3与4.3版本以下版本比较 spjich javahttpclient
    网上利用java发送http请求的代码很多，一搜一大把，有的利用的是java.net.*下的HttpURLConnection，有的用httpclient，而且发送的代码也分门别类。今天我们主要来说的是利用httpclient发送请求。 httpclient又可分为 httpclient3.x httpclient4.x到httpclient4.3以下 httpclient4.3
  • Essential Studio Enterprise Edition 2015 v1新功能体验 Axiba .net
    概述：Essential Studio已全线升级至2015 v1版本了！新版本为JavaScript和ASP.NET MVC添加了新的文件资源管理器控件，还有其他一些控件功能升级，精彩不容错过，让我们一起来看看吧！ syncfusion公司是世界领先的Windows开发组件提供商，该公司正式对外发布Essential Studio Enterprise Edition 2015 v1版本。新版本
  • [宇宙与天文]微波背景辐射值与地球温度 comsci 背景
            宇宙这个庞大,无边无际的空间是否存在某种确定的,变化的温度呢?      如果宇宙微波背景辐射值是表示宇宙空间温度的参数之一,那么测量这些数值,并观测周围的恒星能量输出值,我们是否获得地球的长期气候变化的情况呢?   &nbs
  • lvs-server 男人50 server
    #!/bin/bash # # LVS script for VS/DR # #./etc/rc.d/init.d/functions # VIP=10.10.6.252 RIP1=10.10.6.101 RIP2=10.10.6.13 PORT=80 case $1 in start)   /sbin/ifconfig eth2:0 $VIP broadca
  • java的WebCollector爬虫框架 oloz 爬虫
    WebCollector主页： https://github.com/CrawlScript/WebCollector 下载：webcollector-版本号-bin.zip将解压后文件夹中的所有jar包添加到工程既可。 接下来看demo package org.spider.myspider; import cn.edu.hfut.dmic.webcollector.cra
  • jQuery append 与 after 的区别 小猪猪08
    1、after函数 定义和用法： after() 方法在被选元素后插入指定的内容。 语法： $(selector).after(content) 实例： <html> <head> <script type="text/javascript" src="/jquery/jquery.js"></scr
  • mysql知识充电 香水浓 mysql
    索引 索引是在存储引擎中实现的，因此每种存储引擎的索引都不一定完全相同，并且每种存储引擎也不一定支持所有索引类型。 根据存储引擎定义每个表的最大索引数和最大索引长度。所有存储引擎支持每个表至少16个索引，总索引长度至少为256字节。 大多数存储引擎有更高的限制。MYSQL中索引的存储类型有两种：BTREE和HASH，具体和表的存储引擎相关； MYISAM和InnoDB存储引擎
  • 我的架构经验系列文章索引 agevs 架构
    下面是一些个人架构上的总结，本来想只在公司内部进行共享的，因此内容写的口语化一点，也没什么图示，所有内容没有查任何资料是脑子里面的东西吐出来的因此可能会不准确不全，希望抛砖引玉，大家互相讨论。 要注意，我这些文章是一个总体的架构经验不针对具体的语言和平台，因此也不一定是适用所有的语言和平台的。 （内容是前几天写的，现附上索引）   前端架构 http://www.
  • Android so lib库远程http下载和动态注册 aijuans andorid
    一、背景      在开发Android应用程序的实现，有时候需要引入第三方so lib库，但第三方so库比较大，例如开源第三方播放组件ffmpeg库, 如果直接打包的apk包里面, 整个应用程序会大很多.经过查阅资料和实验，发现通过远程下载so文件，然后再动态注册so文件时可行的。主要需要解决下载so文件存放位置以及文件读写权限问题。   二、主要
  • linux中svn配置出错 conf/svnserve.conf:12: Option expected 解决方法 baalwolf option
    在客户端访问subversion版本库时出现这个错误： svnserve.conf:12: Option expected 为什么会出现这个错误呢，就是因为subversion读取配置文件svnserve.conf时，无法识别有前置空格的配置文件，如### This file controls the configuration of the svnserve daemon, if you##
  • MongoDB的连接池和连接管理 BigCat2013 mongodb
    在关系型数据库中，我们总是需要关闭使用的数据库连接，不然大量的创建连接会导致资源的浪费甚至于数据库宕机。这篇文章主要想解释一下mongoDB的连接池以及连接管理机制，如果正对此有疑惑的朋友可以看一下。 通常我们习惯于new 一个connection并且通常在finally语句中调用connection的close()方法将其关闭。正巧，mongoDB中当我们new一个Mongo的时候，会发现它也
  • AngularJS使用Socket.IO bijian1013 JavaScriptAngularJSSocket.IO
            目前，web应用普遍被要求是实时web应用，即服务端的数据更新之后，应用能立即更新。以前使用的技术（例如polling）存在一些局限性，而且有时我们需要在客户端打开一个socket，然后进行通信。         Socket.IO(http://socket.io/)是一个非常优秀的库，它可以帮你实
  • [Maven学习笔记四]Maven依赖特性 bit1129 maven
    三个模块 为了说明问题，以用户登陆小web应用为例。通常一个web应用分为三个模块，模型和数据持久化层user-core, 业务逻辑层user-service以及web展现层user-web， user-service依赖于user-core user-web依赖于user-core和user-service   依赖作用范围  Maven的dependency定义
  • 【Akka一】Akka入门 bit1129 akka
    什么是Akka Message-Driven Runtime is the Foundation to Reactive Applications In Akka, your business logic is driven through message-based communication patterns that are independent of physical locatio
  • zabbix_api之perl语言写法 ronin47 zabbix_api之perl
    zabbix_api网上比较多的写法是python或curl。上次我用java－－http://bossr.iteye.com/blog/2195679，这次用perl。for example: #!/usr/bin/perl use 5.010 ; use strict ; use warnings ; use JSON :: RPC :: Client ; use
  • 比优衣库跟牛掰的视频流出了，兄弟连Linux运维工程师课堂实录，更加刺激，更加实在！ brotherlamp linux运维工程师linux运维工程师教程linux运维工程师视频linux运维工程师资料linux运维工程师自学
    比优衣库跟牛掰的视频流出了，兄弟连Linux运维工程师课堂实录，更加刺激，更加实在！   ----------------------------------------------------- 兄弟连Linux运维工程师课堂实录-计算机基础-1-课程体系介绍1 链接：http://pan.baidu.com/s/1i3GQtGL 密码：bl65   兄弟连Lin
  • bitmap求哈密顿距离-给定N（1<=N<=100000）个五维的点A(x1,x2,x3,x4,x5)，求两个点X(x1,x2,x3,x4,x5)和Y( bylijinnan java
    import java.util.Random; /** * 题目： * 给定N（1<=N<=100000）个五维的点A(x1,x2,x3,x4,x5)，求两个点X(x1,x2,x3,x4,x5)和Y(y1,y2,y3,y4,y5)， * 使得他们的哈密顿距离（d=|x1-y1| + |x2-y2| + |x3-y3| + |x4-y4| + |x5-y5|）最大
  • map的三种遍历方法 chicony map
    package com.test; import java.util.Collection; import java.util.HashMap; import java.util.Iterator; import java.util.Map; import java.util.Set; public class TestMap { public static v
  • Linux安装mysql的一些坑 chenchao051 linux
    1、mysql不建议在root用户下运行   2、出现服务启动不了，111错误，注意要用chown来赋予权限， 我在root用户下装的mysql，我就把usr/share/mysql/mysql.server复制到/etc/init.d/mysqld, (同时把my-huge.cnf复制/etc/my.cnf)  chown -R cc /etc/init.d/mysql
  • Sublime Text 3 配置 daizj 配置Sublime Text
    Sublime Text 3 配置解释(默认){// 设置主题文件“color_scheme”: “Packages/Color Scheme – Default/Monokai.tmTheme”,// 设置字体和大小“font_face”: “Consolas”,“font_size”: 12,// 字体选项：no_bold不显示粗体字，no_italic不显示斜体字，no_antialias和
  • MySQL server has gone away 问题的解决方法 dcj3sjt126com SQL Server
    MySQL server has gone away 问题解决方法，需要的朋友可以参考下。 应用程序（比如PHP）长时间的执行批量的MYSQL语句。执行一个SQL，但SQL语句过大或者语句中含有BLOB或者longblob字段。比如，图片数据的处理。都容易引起MySQL server has gone away。 今天遇到类似的情景，MySQL只是冷冷的说：MySQL server h
  • javascript/dom:固定居中效果 dcj3sjt126com JavaScript
    <!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd"> <html xmlns="http://www.w3.org/1999/xhtml&
  • 使用 Spring 2.5 注释驱动的 IoC 功能 e200702084 springbean配置管理IOCOffice
    使用 Spring 2.5 注释驱动的 IoC 功能 developerWorks 文档选项 将打印机的版面设置成横向打印模式 打印本页 将此页作为电子邮件发送 将此页作为电子邮件发送 级别： 初级 陈 雄华 ([email protected]), 技术总监, 宝宝淘网络科技有限公司 2008 年 2 月 28 日  &nb
  • MongoDB常用操作命令 geeksun mongodb
    1.   基本操作 db.AddUser(username,password)               添加用户 db.auth(usrename,password)      设置数据库连接验证 db.cloneDataBase(fromhost)    
  • php写守护进程（Daemon） hongtoushizi PHP
    转载自： http://blog.csdn.net/tengzhaorong/article/details/9764655   守护进程（Daemon）是运行在后台的一种特殊进程。它独立于控制终端并且周期性地执行某种任务或等待处理某些发生的事件。守护进程是一种很有用的进程。php也可以实现守护进程的功能。   1、基本概念   &nbs
  • spring整合mybatis,关于注入Dao对象出错问题 jonsvien DAOspringbeanmybatisprototype
    今天在公司测试功能时发现一问题： 先进行代码说明： 1，controller配置了Scope="prototype"（表明每一次请求都是原子型）    @resource/@autowired service对象都可以（两种注解都可以）。 2，service 配置了Scope="prototype"（表明每一次请求都是原子型）
  • 对象关系行为模式之标识映射 home198979 PHP架构企业应用对象关系标识映射
    HELLO!架构   一、概念 identity Map:通过在映射中保存每个已经加载的对象，确保每个对象只加载一次，当要访问对象的时候，通过映射来查找它们。其实在数据源架构模式之数据映射器代码中有提及到标识映射，Mapper类的getFromMap方法就是实现标识映射的实现。     二、为什么要使用标识映射？ 在数据源架构模式之数据映射器中 //c
  • Linux下hosts文件详解 pda158 linux
    　1、主机名： 　　无论在局域网还是INTERNET上，每台主机都有一个IP地址，是为了区分此台主机和彼台主机，也就是说IP地址就是主机的门牌号。 　　公网：IP地址不方便记忆，所以又有了域名。域名只是在公网（INtERNET)中存在，每个域名都对应一个IP地址，但一个IP地址可有对应多个域名。 　　局域网：每台机器都有一个主机名，用于主机与主机之间的便于区分，就可以为每台机器设置主机
  • nginx配置文件粗解 spjich javanginx
    #运行用户#user  nobody;#启动进程,通常设置成和cpu的数量相等worker_processes  2;#全局错误日志及PID文件#error_log  logs/error.log;#error_log  logs/error.log  notice;#error_log  logs/error.log  inf
  • 数学函数 w54653520 java
    public  class  S {        // 传入两个整数，进行比较，返回两个数中的最大值的方法。      public  int  get( int  num1, int  nu
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他