漫谈《集合啦!动物森友会》的大头菜价格趋势与马尔可夫链
前言
还要买更多吗?(曹卖说话有奇怪的口音哈哈哈哈
虽然笔者自己并不是炒菜党,每周只是象征性地囤上五六百棵刷成就里数(以及用来吃),但是大头菜价格背后的细节还是很有些意思的。以下是部分大佬已经做过的工作(orz
- Ninji从游戏中反编译出了(到底是如何做到的呢?)大头菜价格的4种趋势,并形成了C++代码。
- Edricus将上述信息总结成了详尽的文字版:《Breaking Down the Stock Market》。
- lotc.cc上也有一份中文版的说明。
- 开源的JavaScript版大头菜价格预测器Turnip Prophet,GitHub repo在此。
下面先简单复述一下大头菜的价格趋势。
大头菜价格趋势
动森中大头菜价格的4种趋势如下,中文译名似乎已经约定俗成了。
- 0型:Random/Fluctuating(波动型);
- 1型:Large Spike(三期型);
- 2型:Decreasing(下跌型);
- 3型:Small Spike(四期型)。
关于每种趋势的具体数据表现,请参见上面的链接。
在每一周中,大头菜价格的趋势是固定的,直到下个周日曹卖来到岛上时才会变。大头菜的价格在一周间的每天上午、下午都会变动,亦即一周可以分为12期(周一到周六的每个半天)。
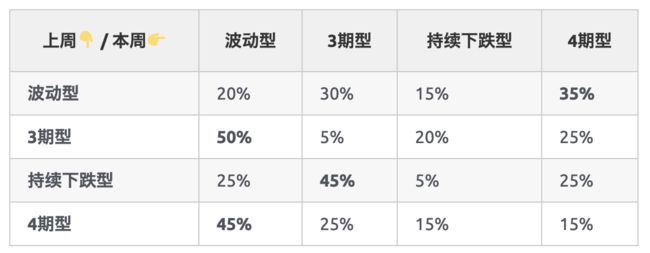
上周的大头菜价格趋势会以一定概率影响本周的价格趋势(玩家初始购买大头菜的那一周默认为四期型),通过代码可以得出概率值如下表。
可见,大头菜价格趋势的变化是一个马尔可夫链,完全符合马尔可夫性质,下面先从数学角度介绍之。
马尔可夫链与马尔可夫性质
以下给出马尔可夫链的形式化定义。
设有随机过程{X(t), t∈T},其中时间T={0, 1, 2, ...},有限状态空间I={i0, i1, i2, ...}。
若对任一时刻n,以及任意I中的状态(j0, j1, ..., jn-1, j, k),均有:
P[X(n+1)=k | X(n)=j, X(n-1)=jn-1, ..., X(1)=j1, X(0)=j0] = P[X(n+1)=k | X(n)=j]
则将X(t)称为一个离散时间马尔可夫链(discrete-time Markov chain, DTMC)。
马尔可夫链是马尔可夫过程(Markov process)在离散时间、有限状态空间条件下的表现,它符合马尔可夫性质(Markov property),即:
X(t)在未来时刻n+1的状态X(n+1)=k只与现在时刻n的状态X(n)=j有关,而与过去的状态X(n-1)=jn-1, ..., X(1)=j1, X(0)=j0全部无关。
这种“未来与过去无关,只与现在有关”的性质非常重要,也被称为“无记忆性”(memorylessness)。看官如果在算法课上深入学习过动态规划的话,会知道动态规划必须满足“无后效性”,它与“无记忆性”是同义词。
转移概率与转移矩阵
说完了定义,再回头看看大头菜价格的特征:
上周的大头菜价格趋势会以一定概率影响本周的价格趋势。
可见确实具有马尔可夫性质,并且是(关于时间)齐次的——亦即它的一步转移概率Pjk = P[X(n+1)=k | X(n)=j]与n的取值无关,而是完全遵循上文表格中给出的概率分布。所以,在Turnip Prophet小程序中,会要求玩家输入上周的大头菜价格趋势。
如果我们将一步转移概率的表格用矩阵的形式表示,就称为一步转移矩阵,如下所示。
一步转移概率和一步转移矩阵是马尔可夫链的核心,很容易推导出齐次马尔可夫链的n步转移矩阵和一步转移矩阵之间的关系:Pn = P1n。根据Chapman-Kolmogorov方程,可以得出:
P(n) = P(0)Pn = P(0)P1n
也就是说,一个马尔可夫链的概率分布完全由它的初始概率分布与一步转移矩阵决定,这是用马尔可夫链进行预测的基础。
遍历性与极限分布
在Turnip Prophet小程序中,如果玩家选择“不知道”上周大头菜的价格趋势,该如何推算出本周趋势价格趋势的概率呢?有了上一节的铺垫,我们先以四期型为初始状态,迭代计算30次趋势的概率分布,Python代码如下。
init = np.array([0.45, 0.25, 0.15, 0.15])
trans_matrix = np.array(
[[0.2, 0.3, 0.15, 0.35],
[0.5, 0.05, 0.2, 0.25],
[0.25, 0.45, 0.05, 0.25],
[0.45, 0.25, 0.15, 0.15]]
)
current = init
for i in range(30):
result = np.dot(current, trans_matrix)
print(i, "\t", result)
current = result
查看输出结果。
0 [0.32 0.2525 0.1475 0.28 ]
1 [0.353125 0.245 0.147875 0.254 ]
2 [0.34439375 0.24823125 0.1474625 0.2599125 ]
3 [0.34682063 0.24706594 0.14766531 0.25844813]
4 [0.34611508 0.24746091 0.14758677 0.25883725]
5 [0.34632692 0.24733093 0.14761437 0.25872778]
6 [0.34626194 0.24737303 0.14760511 0.25875991]
7 [0.34628214 0.24735951 0.14760814 0.2587502 ]
8 [0.34627581 0.24736383 0.14760716 0.25875319]
9 [0.34627781 0.24736246 0.14760748 0.25875226]
10 [0.34627718 0.24736289 0.14760738 0.25875255]
11 [0.34627738 0.24736276 0.14760741 0.25875246]
12 [0.34627731 0.2473628 0.1476074 0.25875249]
13 [0.34627733 0.24736279 0.1476074 0.25875248]
14 [0.34627733 0.24736279 0.1476074 0.25875249]
15 [0.34627733 0.24736279 0.1476074 0.25875248]
16 [0.34627733 0.24736279 0.1476074 0.25875248]
17 [0.34627733 0.24736279 0.1476074 0.25875248]
18 [0.34627733 0.24736279 0.1476074 0.25875248]
19 [0.34627733 0.24736279 0.1476074 0.25875248]
20 [0.34627733 0.24736279 0.1476074 0.25875248]
21 [0.34627733 0.24736279 0.1476074 0.25875248]
22 [0.34627733 0.24736279 0.1476074 0.25875248]
23 [0.34627733 0.24736279 0.1476074 0.25875248]
24 [0.34627733 0.24736279 0.1476074 0.25875248]
25 [0.34627733 0.24736279 0.1476074 0.25875248]
26 [0.34627733 0.24736279 0.1476074 0.25875248]
27 [0.34627733 0.24736279 0.1476074 0.25875248]
28 [0.34627733 0.24736279 0.1476074 0.25875248]
29 [0.34627733 0.24736279 0.1476074 0.25875248]
我们可以发现,4种趋势的概率分布收敛到了[0.34627733 0.24736279 0.1476074 0.25875248]。也就是说,当玩家买入大头菜的次数比较多之后,本周大头菜价格趋势为波动型、三期型、下跌型、四期型的概率分别约为34.6%、24.7%、14.8%和25.9%。这四个值正好就是当玩家选择“不知道”上周大头菜的价格趋势时,预测器使用的概率:
function get_transition_probability(previous_pattern) {
if (typeof previous_pattern === 'undefined' || Number.isNaN(previous_pattern) || previous_pattern === null || previous_pattern < 0 || previous_pattern > 3) {
// TODO: Fill the steady state pattern (https://github.com/mikebryant/ac-nh-turnip-prices/pull/90) here.
return [0.346278, 0.247363, 0.147607, 0.258752];
}
return PROBABILITY_MATRIX[previous_pattern];
}
我们还可以将代码中的初始分布换成其他值,最终会收敛得到一样的结果,这种特性称为马尔可夫链的遍历性。也就是说,如果对状态空间中的一切状态i、j,存在与i无关的常数π(j),使得lim pij(n)=π(j),那么该马尔可夫链就具有遍历性。另外,如果Σ π(j) = 1,那么π(j)叫做转移概率的极限分布。
周中大头菜具体价格的预测
这部分与马尔可夫链的关系就不大了。在根据上周的大头菜价格趋势推断出本周趋势的概率之后,就是根据复杂的随机化算法(假设符合正态分布)对不符合各趋势的价格区间做逐一排除,最终为玩家呈现出可能性最高的价格组合。具体逻辑可以参考Turnip Prophet代码中的predictions.js文件(比较长),以及issues区中的说明与讨论。
The End
明天早起搬砖,民那晚安晚安。