MINP混合整数非线性规划问题求解(MATLAB OPTI toolbox)
MINP(mixed integer nolinear
programming)问题,是运筹学中的难点问题。常用的求解方法有分支定界法,割平面法。混合整数的求解问题已经有一些稳定的求解器。比如ipsolve
cplex, Matlab官方提供的GMATLAB使用智能仿生算法求解该类问题也有不错的稳定度。本文介绍OPTI工具包:
一. 介绍工具OPTI toolbox及其语法
本文介绍 OPTI toolbox 安装方法见:https://github.com/jonathancurrie/OPTI
英文过关的直接按照上面的要求进行安装就可以了。(github如果下载不了,点击这个)
(英文阅读有困难的读:
在上诉网址下载了优化包,之后,需要安装该工具包
安装方法很简单
- 下载
- 点击opti_Install.m 运行该文件
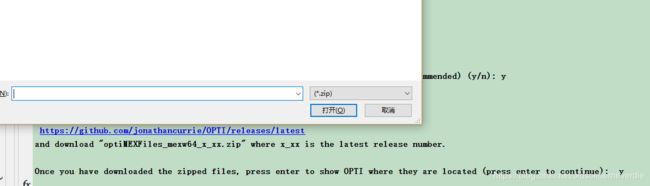
- 到如图的网站中下载 optiMEXFiles_mexw64_x_xx.zip文件
然后继续无脑y
- 程序跳出窗口,选择刚刚下载的文件
- 就可以自动安装了
- 程序会自动解压该压缩包,安装
二、一些case讲解
安装完毕后,对于具体的MINP问题,如何使用该工具来求解呢?
例如:
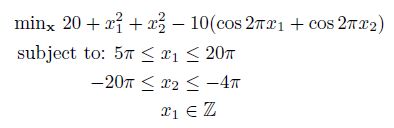
该问题的求解语句为:
%优化的目标函数
fun = @(x) 20 + x(1)^2 + x(2)^2 - 10*(cos(2*pi*x(1)) + cos(2*pi*x(2)))
% 设置约束范围
lb = [5*pi;-20*pi];
ub = [20*pi;-4*pi];
%数据类型,由于原问题中x1是实数,x2为整数,因此xtype='IC'
%必要说明下,I代表interger C代表实数 B 代表{0,1)
xtype = 'IC';
%初始的猜值,OPTI的初始猜值可以不在可行域范围,但会有一定的输出infessible (不可行)的风险
%因此尽量还是设置初始值在可行域中
x0 = [16;0];
% 选项,设定求解器为nomad求解器
opts = optiset('solver','nomad','display','iter')
%创建一个优化对象
Opt = opti('fun',fun,'bounds',lb,ub,'xtype',xtype,'options',opts)
%具体求解该问题
[x,fval,exitflag,info] = solve(Opt,x0)
上述是标准表达,但是对于一般求解的问题而言,目标函数都非常复杂,表达成
fun = @(x) 20 + x(1)^2 + x(2)^2 - 10*(cos(2pix(1)) + cos(2pix(2)))的格式都是非常困难的,表达成子函数是更加合理的做法,同样的,约束条件为x1,x2的形式的也不是很常见。
见下面的问题:

% 目标函数
fun = @(x) x(1)*x(4)*(x(1) + x(2) + x(3)) + x(3);
% 约束条件 (cl <= nlcon(x) <= cu) 设置在cons子函数中
nlcon = @(x) [ x(1)*x(2)*x(3)*x(4);
x(1)^2 + x(2)^2 + x(3)^2 + x(4)^2 ];
cl = [25;40];
cu = [Inf;40]; %对于约束条件的上界和下界,表达成数组的形式,如果是单方向的小于或者大于则表达成 Inf形式
%变量界限 (lb <= x <= ub)
lb = ones(4,1);
ub = 5*ones(4,1);
% 初始猜值
x0 = [1 5 5 1]';
% 求解设置
opts = optiset('solver','ipopt','display','iter');
%建立对象
Opt = opti('fun',fun,'nl',nlcon,cl,cu,'bounds',lb,ub,'x0',x0,'options',opts)
% 求解
[x,fval,exitflag,info] = solve(Opt)
而将目标函数和约束条件都表述成子函数的形式,代码改为:
function main
fun = @obj
%已经将目标函数表达成了子函数的形式
% 约束条件,矩阵形式 (cl <= nlcon(x) <= cu)
nlcon = @cons%约束条件已经表达成了子函数形式
cl = [25;40];
cu = [Inf;40];
%变量的界限 (lb <= x <= ub)
lb = ones(4,1);
ub = 5*ones(4,1);
% 初始的猜值
x0 = [1 5 5 1]';
% 设置求解器选项
opts = optiset('solver','ipopt','display','iter');
% 建立求解对象
Opt = opti('fun',fun,'nl',nlcon,cl,cu,'bounds',lb,ub,'x0',x0,'options',opts)
% 求解
[x,fval,exitflag,info] = solve(Opt)
end
% 目标函数的子函数
function o=obj(x)
o=x(1)*x(4)*(x(1) + x(2) + x(3)) + x(3);
end
%约束条件的子函数
function con=cons(x)
con(1)=x(1)*x(2)*x(3)*x(4);
con(2)=x(1)^2 + x(2)^2 + x(3)^2 + x(4)^2;
end
三、MINP(mixed integer nolinear programming)混合整数线性规划问题求解
由上一节的介绍,我们已经对OPTI toolbox 有了基本的了解。下面对混合整数线性规划MINP问题进行求解。

function main
fun = @obj
%已经将目标函数表达成了子函数的形式
% 约束条件,矩阵形式 (cl <= nlcon(x) <= cu)
nlcon = @cons%约束条件已经表达成了子函数形式
cl = [25;40];
cu = [Inf;40];
%变量的界限 (lb <= x <= ub)
lb = ones(4,1);
ub = 5*ones(4,1);
% 初始的猜值
x0 = [1 5 5 1]';
% 设置求解器选项
%opts = optiset('solver','ipopt','display','iter'); %如果按照这个设定那么输出结果将会错误,因为ipopt不适合求解MINP问题,求解器
%错误,不要设置就好,或者如果对算法有一定了解,选择BONMIN求解。即opts = optiset('solver','BONMIN','display','iter');
opts = optiset('display','iter');
%求解器,如果不确定选什么就不要设定,否则会出问题,OPTI会自动选择合适的求解器
xtype='ICCC' %设置x1是整数对象,其他为实数对象
% 建立求解对象
Opt = opti('fun',fun,'nl',nlcon,cl,cu,'bounds',lb,ub,'x0',x0,'xtype',xtype,'options',opts)
% 求解
[x,fval,exitflag,info] = solve(Opt)
end
% 目标函数的子函数
function o=obj(x)
o=x(1)*x(4)*(x(1) + x(2) + x(3)) + x(3);
end
%约束条件的子函数
function con=cons(x)
con(1)=x(1)*x(2)*x(3)*x(4);
con(2)=x(1)^2 + x(2)^2 + x(3)^2 + x(4)^2;
end
如图则输出结果为:
x =
1.0000
4.7430
3.8211
1.3794
fval =
17.0140
exitflag =
1
info =
Iterations: 0
Nodes: 0
AbsGap: 1.0862e-08
RelGap: 6.3468e-10
Time: 0.0525
Algorithm: 'BONMIN: Branch & Bound using IPOP...'
Status: 'Success'
可以看到OPTI求解MINP问题的是复合的BONMIN算法。事实上,这也是OPTI toolbox自带的为数不多的可以求解MINP问题的求解器了。
以上就是MINP问题用OPTI toolbox求解的案例,实际问题的处理可能包括更多的约束条件和更加复制的目标函数,对上面代码中的约束条件和目标函数子函数进行编辑就可,同时注意对应约束条件的上下界。
笔者用该工具箱处理了复杂的专业问题,稳定性不错,都成功求出了最优解。