硬聚类(HCM)和模糊聚类(FCM)在彩色图像分割中的具体应用
硬聚类(HCM)和模糊聚类(FCM)在彩色图像分割中的具体应用
示例工程见:
http://files.cnblogs.com/laviewpbt/%e5%9b%be%e5%83%8f%e6%a8%a1%e7%b3%8a%e8%81%9a%e7%b1%bb.rar
一年前我写过模糊聚类算法(FCM)和硬聚类算法(HCM)的VB6.0实现及其应用 一文,之后,有不少同仁向我询问如何将这个算法应用在彩色图像的分割上,鉴于图像数据的特殊性,这里简单的谈谈在图像中聚类算法的需要注意一些细节。
C均值聚类算法较其他的聚类算法的主要优点是可以对大数据量进行计算(我也写过基于模糊等价关系的模糊聚类分析 ,这个方法只能分析很小的数据量),并且理论上已经证明该算法是收敛的。因此,对于图像的分割,特别是多于2类的彩色图像分割(2类的分割即二值化的过程,已经有着很多的方法,参见几种经典的二值化方法及其vb.net实现 ,但是这些方法很难扩展的多类分割中),有着广泛的应用。
我们知道,彩色图像的数据可以看成一M*N*3的数组,但是一方面三维数组的处理速度要低于一维或二维数组,另外从FCM通用性上讲,一般要分割的对象为样本组,而一个样本可以看成是n维空间中的一个点,因此,用二维数组来描述要分割的对象不仅意义明显而且有利于计算速度的提高。在MATLAB以及前面我写的那个FCM函数中第一维是样本,第二维是样本的具体数据,但是,图像数据在内存中的排列方式是BGRABRGABGRA.......(32位的),这样,通过API函数直接读取的数据一般为一(1 to 4,1 to M*N)数组,因此,要把前面写的那个FCM函数应用于图像分割,首先要改变下函数内部分循环的次序,这是其一。
彩色图像的数据量非常之大,要使得FCM或HCM函数具有实用价值,就必须把握好函数的每一个细节。下面我就在实际中我遇到的几个问题向大家描述下。
1、初始中心的选取
初始中心的选取其否合理直接影响着计算的速度和结果。不合理的初始点,可能导致结果收敛至一个不希望的极小点。这里提供几个选取初始中心点的方法以供参考。
- 随机值 当我们对样本的来源或分布没有任何的先验知识时,这不失为一种上策,但是要注意不要超过已知数据的分布范围,比如对于图像数据,可以用rnd*255保证数据在(0~255)之间。但是这种方法的计算速度是相当缓慢的。
- 从已知数据中随机的选几个 这种方法要比第一种稍微合理点,以已知的数据点为中心也要更加透明点。
- 从已知数据按等距离选区几个点 类似于上述方法
- 均值-标准差法 。根据随机函数的分布知识,聚类的数据应主要分布在所有数据的均值附近。标准差是评价数据分布的又一重要指标,假设所有数据的均值为μ,标准差为σ,则数据应该主要分布在(μ-σ,μ+σ)之间。假设分类数为N,选择初始分类点为(μ-σ,μ+σ)之间的N 个等分点进行分类。图像数据可以分别在R/G/B上做上述计算,实际运行的结果也表明这种方法在大多数情况下要比上述三种方法速度快。
- 从缩略图得到中心 这一方法是专门针对图像的,通过先在一定大小缩略图中进行聚类,得到初始聚类中心,因为缩略图在数据可以看成原始数据的压缩,并且这种压缩对聚类中心的影响很小,而且生成缩略图有高速的算法,同聚类相比,所需要的时间可以不计。
- 手工输入数据 针对具体的一些列图像,比如医学图像,我们一般情况下能够知道大概的聚类中心,这样通过人工指定初始聚类中心使得其和最终的中心接近以加快速度。
- 对于FCM算法,还可以先用HCM产生中心点。
2. 样本空间的选取
- 通常情况下,我们可以直接使用R|G|B值作为待聚类的数据。
- 如果考虑噪音的影响,可以先滤波或者选择恰当的模板(比如3*3加权模板)生成的数据作为聚类数据源。
- 采用HSB或其他颜色空间的数据
- 对于彩色图像的数据,实际上有很多像素的颜色是一样的,这样采用对数据压缩、合并的方法, 减少参与计算的数据量, 降低运算开销, 极大地减少FCM算法每次迭代过程的时间, 提高计算速度。我们先计算出图像中实际使用的不同的颜色数以及每个颜色数所具有的像素数量,则在迭代中需要计算的数据量大为减少。但是这种方法对于HCM可能不是很合适,下面将继续讨论。
3. 距离的定义方式
不同的定义方式体现了不同的分割思想,以下是常用的集中距离定义方式。
- 欧式距离(Euclidean Distance)
(1)相信大家对这个距离公式是非常熟悉的,初中时就学了,也称它为两点间的距离。p和q之间的欧式距离定义如下:
De(p , q) = [(x - s)2 + (y - t)2]1/2
(2)距离直观描述:距点(x , y)小于或等于某一值r的欧式距离是中心在(x , y)半径为r的圆平面。 - 城区距离(City-Block Distance)
(1)p和q之间的城区距离定义如下:
D4(p , q) = |x - s| + |y - t|
(2)距离直观描述:距点(x , y)小于或等于某一值r的城区距离是中心在(x , y)对角线为2r的菱形。 - 棋盘距离(Chess Board Distance)
(1)p和q之间的棋盘距离定义如下:
D8(p , q) = max(|x - s| , |y - t|)
(2)距离直观描述:距点(x , y)小于或等于某一值r的棋盘距离是中心在(x , y)对角线为2r的正方形。
详见:http://www.ownsoft.com/blog/blogview.asp?logID=48
4. 优化技巧
- 利用临时数组保存常用的一些计算值,比如在才采用城区距离和棋盘距离时,定义TempArray数组并赋值如下:
For i = -255 To 255
TempArray(i) = Abs(i)
Next
这样比直接在代码里用abs函数效率要高很多,即使用下述代码
Dist = TempArray(Data(1, i) - OldCenter(j, 1)) + TempArray(Data(2, i) - OldCenter(j, 2)) + TempArray(Data(3, i) - OldCenter(j, 3))
代替语句:
Dist = Abs(Data(1, i) - OldCenter(j, 1)) + Abs(Data(2, i) - OldCenter(j, 2)) + Abs(Data(3, i) - OldCenter(j, 3))
一个误区 :我曾在计算欧式距离的时候也定义了一个256个元素的数组记录n^2,然后用数组代替n*n计算,结果发现这样会导致计算速度的下降,所以在VB中这种简单的加减乘除还是很快的,只有在用像abs,Exp等函数时,如果方便在事前计算好查找表才会加快速度。
- 中间的二维数组变量全部用一维数组代替,同样的数据量一维数组要快些,这样大约可以提速10%。
- 用n*n代替n^2,用 Exp(Log(Degree(i, j)) * Exponent)代替Degree(i, j)^Exponent,可能时用右除代替左除。对于大量循环中的这种运算,前者的速度绝对要比后者快很多。
- 不要偷懒用for k=1 to 3 ,要手工展开每一项
- 最小收敛距离取12的理由是 2^2+2^2+2^2,取得更小没有意义,因为图像数据的聚类中心始终是整型。同样,在大部分的数据类型的选择中,都可以用整型代替双精度型。
下面以部分分割效果来说明上述问题:
可以看出,采用随机中心,特别是对于FCM算法,要经过很长时间才能收敛。
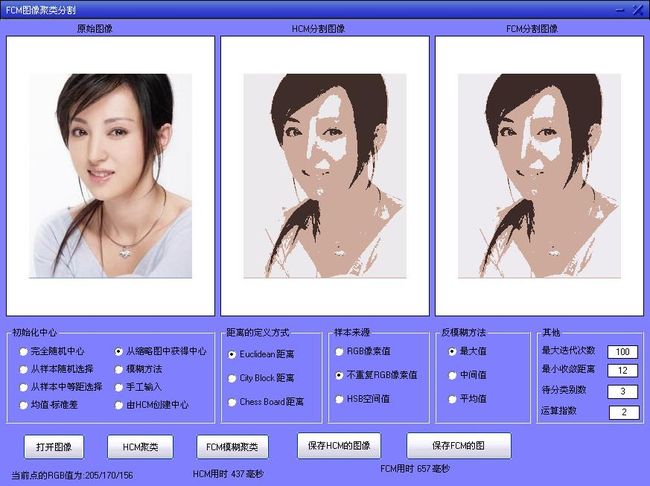
对美女分类, 采用从缩略图获得中心、样本来源于RGB像素值。HCM用时0.25s,FCM用时1s。
其他条件不变,样本来源选择不重复的RGB像素值,HCM用时增加为437ms,FCM用时降低为657ms,这是因为针对这幅图像,HCM算法中分析不重复颜色值所需要的时间增量比循环时所节省时间要多,而FCM算法由于其循环的复杂度要高很多,当减小循环量时节省的时间特别明显。
一般情况下,一副彩色图像中不重复的颜色值和总的像素个数的比例可以达到1:5,当这个比值越明显的时候,采用不重复的RGB像素值时则速度提升越明显,特别是对于FCM算法,时间可以降为原来的1/3左右。